目前进度:6/8
CF1341A
题意简述
现在有 \(n\) 个数,每个数的大小在 \([a-b,a+b]\) 内,问是否存在一种情况,使得这 \(n\) 个数的和在 \([c-d,c+d]\) 内。
多测,\(t\le 1000,0\le b<a\le 1000,0\le d<c\le 1000\)
算法分析
不难发现,这 \(n\) 个数的和的最小值为 \((a-b)n\),和的最大值为 \((a+b)n\) ,且范围内的每一个和都可以构造。
因此只要区间 \([(a-b)n,(a+b)n]\) 与 \([c-d,c+d]\) 有交集即可。
代码实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
int n,a,b,c,d;
signed main(){
int T;
read(T);
while(T--){
read(n);read(a);read(b);read(c);read(d);
int al=(a-b)*n,ar=(a+b)*n;
int bl=(c-d),br=(c+d);
if(ar<bl||al>br)puts("NO");
else puts("YES");
}
return 0;
}
CF1341B
题意简述
给定一个长度为 \(n\) 的数组\(a_i\)。定义一个位置 \(i\) 是“峰”,当且仅当 \(a_{i-1}\le a_i \ge a_{i+1}\)。
求长度为 \(k\) 的区间中含有“峰”个数最多的区间。
多测,\(1\le t\le 10^4,3\le k\le n\le 2\times10^5,0\le a_i\le 10^9,\sum n\le 2\times 10^5\)。
算法标签
前缀和,模拟
算法分析
我们可以预先处理出每个位置是否可能为“峰”,然后取区间长度为 \(k\) 的包含“峰”最多的区间,这个可以借助前缀和 \(O(1)\) 求出。
注意每个区间的边界位置不能算做“峰”。
代码实现
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define maxm 2000005
#define inf 0x3f3f3f3f
#define LL long long
#define mod 1000000007
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
int n,m;
int a[maxn],b[maxn],s[maxn];
int posl,ans;
signed main(){
int T;
read(T);
while(T--){
read(n);read(m);
for(int i=1;i<=n;++i)read(a[i]);
for(int i=1;i<=n;++i){
if(i==1||i==n)b[i]=0;
else{
if(a[i-1]<=a[i]&&a[i+1]<=a[i])b[i]=1;
else b[i]=0;
}
}
for(int i=1;i<=n;++i)s[i]=s[i-1]+b[i];
posl=0,ans=-1;
for(int l=1;l+m-1<=n;++l){
int tmp=s[l+m-2]-s[l]+1;
if(tmp>ans){
posl=l;ans=tmp;
}
}
printf("%d %d\n",ans,posl);
}
return 0;
}
CF1340A
题意简述
有一个随机数生成器。
- 定义 \(r_j\) 表示 \(j\) 右边(包括 \(j\) )第一个没有标记的位置。
- 定义 \(count_j\) 表示满足 \(r_i=j\) 的 \(i\) 的个数。
- 刚开始所有位置都没有被标记。
它的工作方法如下:
- 找到当前 \(count\) 值最大且没有被标记的位置 \(i\) ,如有多个 \(i\) ,则随机选取一个。
- 标记 \(i\) 的位置,并将输出序列的第 \(i\) 项设为已经被标记的位置的数量。
- 如果还有数没有被标记,重复执行第一步。
判断一个排列是否有可能是这个生成器生成的。
多测,\(t\le 10^5,1\le n\le 10^5,\sum n\le 10^5\)。
算法标签
并查集,可修改堆/线段树/其他数据结构。
算法分析
分析 \(r_j\) 的修改过程,发现其与并查集类似,且\(count_j\)对应并查集集合大小。
我们只需要判断当前输出的数是否是 \(count\) 值最大且没有被标记即可,这个最大值可以通过堆或者线段树等数据结构求得。
代码实现
写的比较丑……
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define maxm 2000005
#define inf 0x3f3f3f3f
#define LL long long
#define mod 1000000007
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
int n,m;
int a[maxn];
int fa[maxn],siz[maxn];
int fid(int x){
return fa[x]==x?fa[x]:fa[x]=fid(fa[x]);
}
void merge(int x,int y){//x->y
int xx=fid(x),yy=fid(y);
if(xx==yy)return;
fa[xx]=yy;siz[yy]+=siz[xx];
}
int mx;
set<int>st;
#define lson ((x<<1))
#define rson ((x<<1)|1)
#define mid ((l+r)>>1)
int str[maxn<<2];
void pushup(int x){
str[x]=max(str[lson],str[rson]);
}
void chg(int x,int l,int r,int p,int v){
if(l==r){
str[x]=v;
return;
}
if(p<=mid)chg(lson,l,mid,p,v);
else chg(rson,mid+1,r,p,v);
pushup(x);
}
int get_max(){
return str[1];
}
void upd(int p,int v){
chg(1,1,n,p,v);
}
signed main(){
int T;
read(T);
while(T--){
read(n);mx=1;
for(int i=1,x;i<=n;++i)read(x),a[x]=i;
for(int i=1;i<=n;++i)fa[i]=i,siz[i]=1;
int fl=1;st.clear();
for(int i=1;i<=n;i++)st.insert(i),upd(i,1);
for(int i=1;i<=n;++i){
int cur=a[i];
int mx=get_max();
if(siz[cur]!=mx){
fl=0;break;
}
st.erase(cur);
set<int>::iterator nxt=st.lower_bound(cur);
if(nxt!=st.end()){
int y=(*nxt);
merge(cur,y);
upd(y,siz[y]);
upd(cur,0);
}
else{
fa[cur]=siz[cur]=0;
upd(cur,0);
}
}
puts(fl?"YES":"NO");
}
return 0;
}
CF1340B
题意简述
有 \(n\) 个如下图所示的灯组原件,构成了一个计分板。每个灯组原件由 \(7\) 个灯管组成,编号如下图所示。
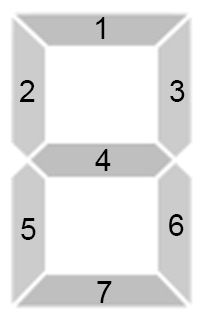
现在这 \(n\) 个灯组原件中,有一些灯管保持常亮,求再点亮恰好 \(k\) 个灯管,能够组成的最大的数是多少。
答案允许有前导零。
\(1\le n\le 2000,0\le k\le 2000\)。
算法标签
贪心 dp
算法分析
首先考虑直接从前向后贪心,尽可能选较大的数。
这时我们发现一个问题:这样的贪心可能最后无解。
无解?那就不让它无解!
考虑反向dp判断可行性,\(dp(i,j)\)表示 \(i\) 到 \(n\) 的灯组再点亮 \(j\) 个是否能构成数字。
这是一个比较经典的背包可行性问题,可以以 \(O(nk)\) 的时间复杂度求出答案。
这样我们在从前向后的贪心过程中在保证有解的同时让数字尽可能大即可。
总时间复杂度 \(O(nk)\) 。
代码实现
可以把输入转化为二进制处理较为方便。
#include<bits/stdc++.h>
using namespace std;
#define maxn 2005
#define maxm 2000005
#define inf 0x3f3f3f3f
#define LL long long
#define mod 1000000007
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
int n,m;
int a[maxn];
int nm[]={119,18,93,91,58,107,111,82,127,123};
int cst[maxn][10];
int siz[200];
int dp[maxn][maxn];
signed main(){
read(n);read(m);
for(int i=1;i<=127;++i)siz[i]=siz[i-(i&(-i))]+1;
for(int i=1,x;i<=n;++i){
for(int j=6;~j;--j){
scanf("%1d",&x);
if(x)a[i]|=(1<<j);
}
for(int j=0;j<10;++j){
if((a[i]&nm[j])==a[i]){
cst[i][j]=siz[nm[j]^a[i]];
}
else{
cst[i][j]=-1;
}
}
}
//可行性dp
dp[n+1][0]=1;
for(int i=n;i;--i){
for(int j=0;j<=m;++j){
for(int k=0;k<10;++k){
if(~cst[i][k]){
if(j>=cst[i][k])dp[i][j]|=dp[i+1][j-cst[i][k]];
}
}
}
}
//贪心
for(int i=1;i<=n;++i){
int fl=-1;
for(int k=9;~k;--k){
if(cst[i][k]==-1)continue;
if(dp[i+1][m-cst[i][k]]){
fl=k;break;
}
}
if(fl==-1){
puts("-1");
return 0;
}
printf("%d",fl);
m-=cst[i][fl];
}
return 0;
}
CF1340C
题意简述
在\([0,n]\)范围内有\(m\)个安全岛,保证 \(0,n\) 两个整点是安全岛。
从 \(0\) 出发,每秒钟可以从 \(x\) 移动到 \(x−1\) 或 \(x+1\),注意只能在安全岛改变移动方向。
有一个红绿灯,绿灯时间为 \(g\) 秒,红灯时间为 \(r\) 秒。在绿灯时间内必须移动,在红灯时间内必须在某个安全岛停留。出发时红绿灯刚从红灯变为绿灯。
求从 \(0\) 到 \(n\) 的最短时间。
\(1\le n\le 10^6,1\le g,r\le 10^3,1\le m\le 10^4\)。
算法标签
dp 01bfs
算法分析
我们称一次绿灯和一次红灯为一个周期,则走到\(n\)应当是若干个完整周期和1个不完整周期。
设 \(dp(x,i)\) 表示从 \(0\) 走到 \(x\) 所需要的最少周期个数。
分类讨论从一个安全岛到另一个安全岛的可能情况,不难发现只需要考虑相邻安全岛的转移情况即可覆盖所有的状态。
设两个相邻的安全岛 \(x,y\) ,距离为 \(w\) ,现在要从 \(x\) 转移到 \(y\),下面讨论对于一个不完整周期的时间 \(i\) 的转移(即 \(dp(x,i)\) 到 \(dp(y,?)\) 的转移)。
- \(i+w<m\) 仍然在同一个周期内,周期数不变,\(dp(y,i+w)<-dp(x,i)\);
- \(i+w=m\) 这时一个周期结束,周期数+1且不完整周期为 \(0\) ,\(dp(y,0)<-dp(x,i)+1\);
- \(i+w>m\) 由题意知,这时如果从 \(x\) 转移到 \(y\) 中间会有红灯,且无法在安全岛停留,故无法转移。
观察这个转移,发现转移方向是双向的,因此转移带环。带环dp的最优化问题一般看作最短路,本题因为转移权值为 \(0/1\) ,可以使用 01bfs 。
时间复杂度 \(O(mg)\) 。
代码实现
注意恰好走完一个周期不需要再等红灯。
#include<bits/stdc++.h>
using namespace std;
#define maxn 10005
#define maxm 1005
#define inf 0x3f3f3f3f
#define LL long long
#define mod 1000000007
#define local
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);}
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
int N,n,m,R;
int a[maxn];
int dp[maxn][maxm];
struct node{
int id,tm;
};
deque<node>q;
void bfs(){
memset(dp,0x3f,sizeof(dp));
dp[1][0]=0;q.push_back((node){1,0});
while(!q.empty()){
int x=q.front().id,t=q.front().tm;q.pop_front();
if(x>1){
int y=x-1,w=a[x]-a[x-1];
if(t+w==m){
if(dp[y][0]>dp[x][t]+1){
dp[y][0]=dp[x][t]+1;
q.push_back((node){y,0});
}
}
if(t+w<m){
if(dp[y][t+w]>dp[x][t]){
dp[y][t+w]=dp[x][t];
q.push_front((node){y,t+w});
}
}
}
if(x<n){
int y=x+1,w=a[x+1]-a[x];
if(t+w==m){
if(dp[y][0]>dp[x][t]+1){
dp[y][0]=dp[x][t]+1;
q.push_back((node){y,0});
}
}
if(t+w<m){
if(dp[y][t+w]>dp[x][t]){
dp[y][t+w]=dp[x][t];
q.push_front((node){y,t+w});
}
}
}
}
}
signed main(){
read(N);read(n);
for(int i=1;i<=n;++i)read(a[i]);
read(m);read(R);
sort(a+1,a+n+1);
bfs();
int mn=inf;
for(int i=0;i<=m;++i){
if(dp[n][i]==inf)continue;
int tmp=dp[n][i]*(m+R)+i;
if(i==0)tmp-=R;
mn=min(mn,tmp);
}
if(mn==inf)puts("-1");
else printf("%d\n",mn);
return 0;
}
CF1340D
题意简述
给你一棵树,通过每条边需要 \(1\) 的时间,你可以在一个结点处将时间变为任意一个比当前时间小的非负整数。现在要从 \(1\) 号节点从时间 \(0\) 出发,经过所有的节点并返回 \(1\) 号节点,要求不能两次在同一时间在同一个节点。求一种方案使得每个点的最大时间最小。
算法标签
树上问题 dfs 构造
算法分析
不难发现答案的下界是度数最大的节点的度数(最优情况下每个节点都要经过 \(deg+1\) 次,因此至少要填上 \(0,1,\cdots,deg\) 这些数字)
下面我们考虑直接构造出满足下界的答案。
为了方便构造,若进入节点 \(x\) 的时间点为 \(t_x\) ,则离开节点 \(x\) 的时间点必须为 \(t_x-1\) (这样返回节点 \(x\) 的父节点时间点就为 \(t_x\) )。
在遍历节点 \(x\) 的所有子节点时可能会有如下两种情况:
- \(t_x+deg_x<maxdeg\) 则过程中不会超过答案,只需遍历结束后将时间回到 \(t_x-1\) 即可。
- \(t_x+deg_x\ge maxdeg\) 过程中会有某一个节点的时间点超过答案。因为总共会占用 \(deg_x+1\) 个时间点,因此当过程中的标号达到 \(maxdeg\) 时只需回到 \(maxdeg-deg_x\) 的时间点即可。
注意一些实现上的细节即可,时间复杂度 \(O(n)\) 。
代码实现
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define maxm 2000005
template <typename Tp>void read(Tp &x){
x=0;int fh=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-'){fh=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=fh;
}
int n,m;
vector<int>G[maxn];
struct oper{
int id,tm;
}ans[maxm];
int tot;
int du[maxn],md;
void dfs(int x,int pa,int tim){
int curt=tim;
ans[++tot]=(oper){x,tim};
if(curt==md){
curt-=du[x];
ans[++tot]=(oper){x,curt};
}
for(unsigned i=0;i<G[x].size();++i){
int y=G[x][i];
if(y==pa)continue;
dfs(y,x,++curt);
ans[++tot]=(oper){x,curt};
if(curt==md&&i!=G[x].size()-1){
curt-=du[x];
ans[++tot]=(oper){x,curt};
}
}
if(x!=1&&curt!=tim-1){
ans[++tot]=(oper){x,tim-1};
}
}
signed main(){
read(n);
if(n==1){
puts("1");
puts("1 0");
return 0;
}
for(int i=1,x,y;i<n;++i){
read(x);read(y);
G[x].push_back(y);
G[y].push_back(x);
++du[x];++du[y];md=max(md,du[x]);md=max(md,du[y]);
}
dfs(1,0,0);
printf("%d\n",tot);
for(int i=1;i<=tot;++i){
printf("%d %d\n",ans[i].id,ans[i].tm);
}
return 0;
}


