L. Two Buildings【分治+决策单调性优化】

题目链接

题意：给你N个h[i]，求(ℎ𝑖+ℎ𝑗)∗(𝑗−𝑖)的最大值。

题外话：比赛的时候去写了模拟和I，二过一，最后没时间写这个了，然后补题时候做掉了。

思路：可以看到1≤h_i≤10⁶，所以，我们不妨令原式变成(h_i - (-h_j)) * (j - i)，这样就变成了求四边形面积的最大值了。

我们可以做几个推论：

  如果，有i₁<i₂，则容易发现，当h[i₁] ≥ h[i₂]时候，i₂是不产生贡献的，因为对于i < j，如果存在一个点，作为四边形的左上角，它不仅更靠左，而且还更靠上，那么显然另一个就没有用了。

  同理，我们对j也有同样的性质。

  接下去，就是分析对于有i₁<i₂，当h[i₁] < h[i₂]时候的情况了。

  如图，可以看成这样的情况：

 

 

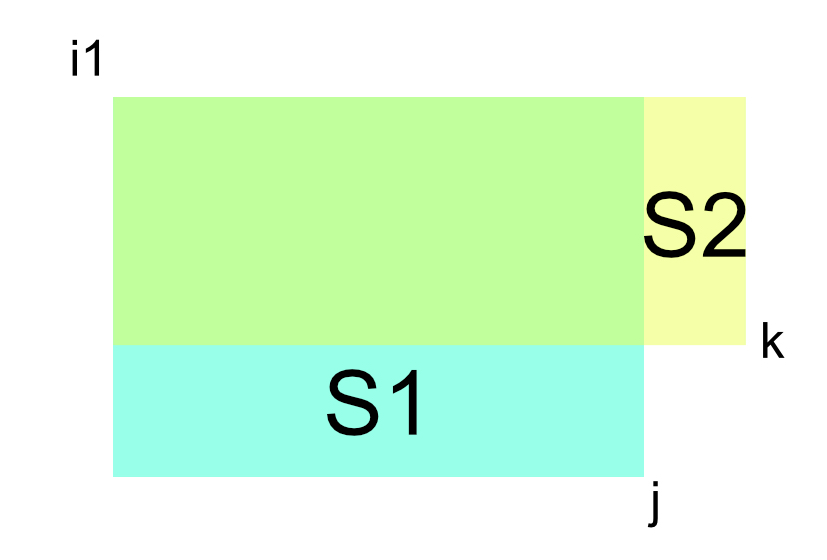
对于i₁点，我们可以假定，选j点比选择k点更优，除去相同的面积，我们可以认为S1>S2。

 

如果此时有个存在于i₁之前的i₂点，那么，可以发现有如下图所示：

 

 

 

 

有，S1 > S2可得，S1 + S3 > S2 - S4，所以对于i₂来说，可能的更优点不会存在于j的右边，只可能存在于j的左边，所以我们直接去搜索[1, j]即可。

同理，如果存在一点i₁<i₂，也就是当i₂出现于i₁的后面时候，我们应该去搜索[j, N]的范围，寻找是否存在更优解。

所以，我们为了优化复杂度，不妨假设一点i，为区间的中间值mid，然后我们再去看左边的值应当搜索的范围，以及右边的值应当搜索的范围。于是，可以利用分治的做法解决这类问题。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <limits>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <bitset>
#include <unordered_map>
#include <unordered_set>
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
#define pii pair<int, int>
#define MP(a, b) make_pair(a, b)
using namespace std;
typedef unsigned long long ull;
typedef unsigned int uit;
typedef long long ll;
const int maxN = 1e6 + 7;
int N;
ll h[maxN];
int cnt_a = 0, cnt_b = 0;
struct node
{
    ll x, y;
    node(ll a=0, ll b=0):x(a), y(b) {}
} a[maxN], b[maxN];
ll Area(node e1, node e2) { return (e2.x - e1.x) * (e1.y - e2.y); }
ll ans = 0;
void cdq(int l, int r, int ql, int qr)
{
    if(l > r || ql > qr) return;
    int mid = HalF, pos = qr;
    ll tmp = Area(a[mid], b[pos]);
    for(int i = ql; i <= qr; i ++)
    {
        if(Area(a[mid], b[i]) > tmp)
        {
            tmp = Area(a[mid], b[i]);
            pos = i;
        }
    }
    ans = max(ans, tmp);
    if(l < mid) cdq(l, mid - 1, ql, pos);
    if(r > mid) cdq(mid + 1, r, pos, qr);
}
int main()
{
    scanf("%d", &N);
    for(int i = 1; i <= N; i ++) scanf("%lld", &h[i]);
    ll pos = 0;
    for(int i = 1; i <= N; i ++)
    {
        if(h[i] > pos)
        {
            pos = h[i];
            a[++ cnt_a] = node(i, h[i]);
        }
    }
    pos = 0;
    for(int i = N; i >= 1; i --)
    {
        if(-h[i] < pos)
        {
            pos = - h[i];
            b[++ cnt_b] = node(i, - h[i]);
        }
    }
    for(int i = 1, j = cnt_b; i < j; i ++, j --) swap(b[i], b[j]);
    cdq(1, cnt_a, 1, cnt_b);
    printf("%lld\n", ans);
    return 0;
}