一旦得到平面方程,就可以进行射线/多边形的交点。在计算射线/平面交叉后,下一步是确定交点是否在多边形内。
有许多不同的方法可以解决这个问题。Berlin[1]很好地概述了一些技术。这里给出的方法是在[14]中提出的“射线相交”算法的一个修改版本。该算法的工作原理是,从交点处向任意方向发射一束射线,并计算相交的线段数。如果交叉的数目是奇数,则点在多边形内;其他外。这就是所谓的Jordan曲线定理。图6描述了这个定理的用法。下面提出的改进算法优雅地处理了测试光线与多边形顶点相交的特殊情况。这是我自己的发明,似乎是一个最佳的解决方案。
以点集定义定义多边形:
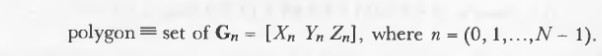
定义平面:
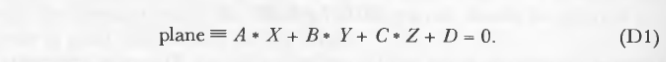
定义平面的法线(非必要法线):
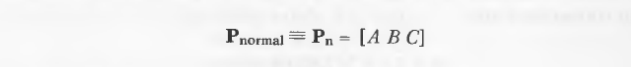
平面与光线的交点:

第一步是将多边形投射到二维平面上。在这个平面中,所有的点都由一对(U,V)指定。所以,我们想要的是每个[X Y Z]坐标都对应一个(U,V)。
一种方法是将平面绕一些轴旋转,直到法线与其他轴平行(比如Z)。在这之后,剩下的两个轴(在这个例子中是X和Y)可以用来生成(U,V)对。该方案的缺点是必须为每个多边形生成和存储一个旋转矩阵,并且必须为每个坐标执行一个矩阵乘法。
这些成本可以通过简单地丢弃[X Y Z]其中一个坐标并使用另外两个来消除。这个动作将多边形投射到由两个选定的坐标定义的平面上。多边形的面积没有保留,但是拓扑结构保持不变。选择扔掉哪个坐标的定义如下:扔掉绝对值最大的坐标。例如,对于一个Pn=[0 -5 3]的多边形,Y坐标会被丢弃,X和Z被分配给U和V (U和V是任意的)。我们将用最大的坐标作为主导坐标。
一旦多边形被投射到平面上,内外测试就相当简单了。平移多边形使交点在原点,即从每个顶点减去交点的坐标(Ui Vi)。将这些新顶点标记为(U',V')。现在想象一条光线从原点出发沿着+U轴运动。对多边形的每条边进行相交测试。如果边缘穿过光线,记录下来。如果相交的总数是奇数,则点在多边形内。这个操作如图7所示。
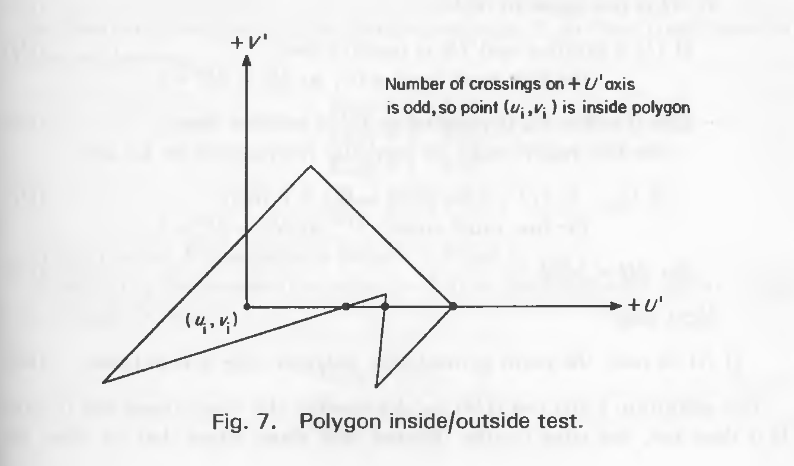
正如Berlin[1]所指出的那样,在光线上的顶点必须作为特殊的情况来处理。这些特殊情况可以通过定义它们的方式来避免。沿着+U'轴延伸的光线将平面分成两部分。然而,也有一些点在U轴上。必须对位于光线上的顶点(即V' = 0)添加声明,定义其位于+ V'端。这样光线上就没有点了,特殊情况就消失了。光线本身必须被重新定义为无限接近原始光线,但不能通过任何点。它现在是一条分界线,而不是一系列的点。

算法的第一次测试(D4)检查两顶点的v是否符号不同。如果符号相同,则可以忽略(因为v符号相同则不会与u交叉)。如果两U都大于0,那么+U'轴必然与其交叉(D5)。否则,如果端点中的任何一个U>0(D6),则必须找到边与U'轴相交的准确U'位置(即此直线与U+的截距)。如果(D7)这个截距为正(即在+U'轴上),那么这条边确实与+U'相交。
该方法比较高效,因为大多数边缘可以被平凡地拒绝或接受。 只有当边缘从对角象限延伸时才需要进行严格的计算。
这个和其他内-外部测试算法的一个小问题是,在边缘上的相交点被任意地决定在内部或外部。这个问题是有解决办法的,但是在实践中,边缘上的交点大多是不相关的。这是因为,如果一个交点落在两个多边形之间的边缘上,并且两个多边形都投影在同一个平面上,那么算法就会确定这个点在一个多边形内,并且只在其中一个多边形内(不考虑精度误差).
在图6中,五角星的中心五边形不被考虑在恒星内部,因为交叉的数量是偶数。多边形的另一个定义是将这些点考虑到多边形内部。
要对这类多边形进行内外测试,需要对之前的算法做一个简单的修改。改变的是当+U'轴的边从+V'传递到-V'时增加NC,从-V'传递到+V'时减少NC。如果NC是0,点在多边形外面,否则它在多边形里面。
数字NC被称为圈数。想象这个多边形是由绳子构成的,一个铅笔点被放在交点上。如果弦被拉紧,圈数就是弦绕点的次数。NC的符号是旋转的方向:‘+’是顺时针,‘-’是逆时针。



