什么是辗转相除法(欧几里得算法)
参考内容(https://baike.baidu.com/item/欧几里得算法/1647675?fr=ge_ala)
两个整数的最大公约数是能够同时整除它们的最大的正整数。辗转相除法基于如下原理:两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数。
算法说明
参考文章(https://www.cnblogs.com/wangqi3206/p/15492916.html)
输入两个数字a和b
判断a<b是否为真
如果结果为真,则交换a和b的值,进入下一个判断
如果结果为假,则进入下一判断
判断b=0是否为真
如果结果为真,则a就是a,b的最大公约数,输出a
如果结果为假,则下一步
将a%b的结果赋给变量c(取余数)
判断c=0是否为真
若结果为假,则先将b的值赋给a,再将c的值赋给b,重新进入c=a%b
若结果为真,则b就是a,b的最大公约数,输出b
结束
伪代码实现
INPUT a,b
WHILE a < b
temp = a
a = b
b = temp
IF b = 0
print a
ELSE
c = a % b
WHILE c != 0
a = b
b = c
print b
运算结果与截图
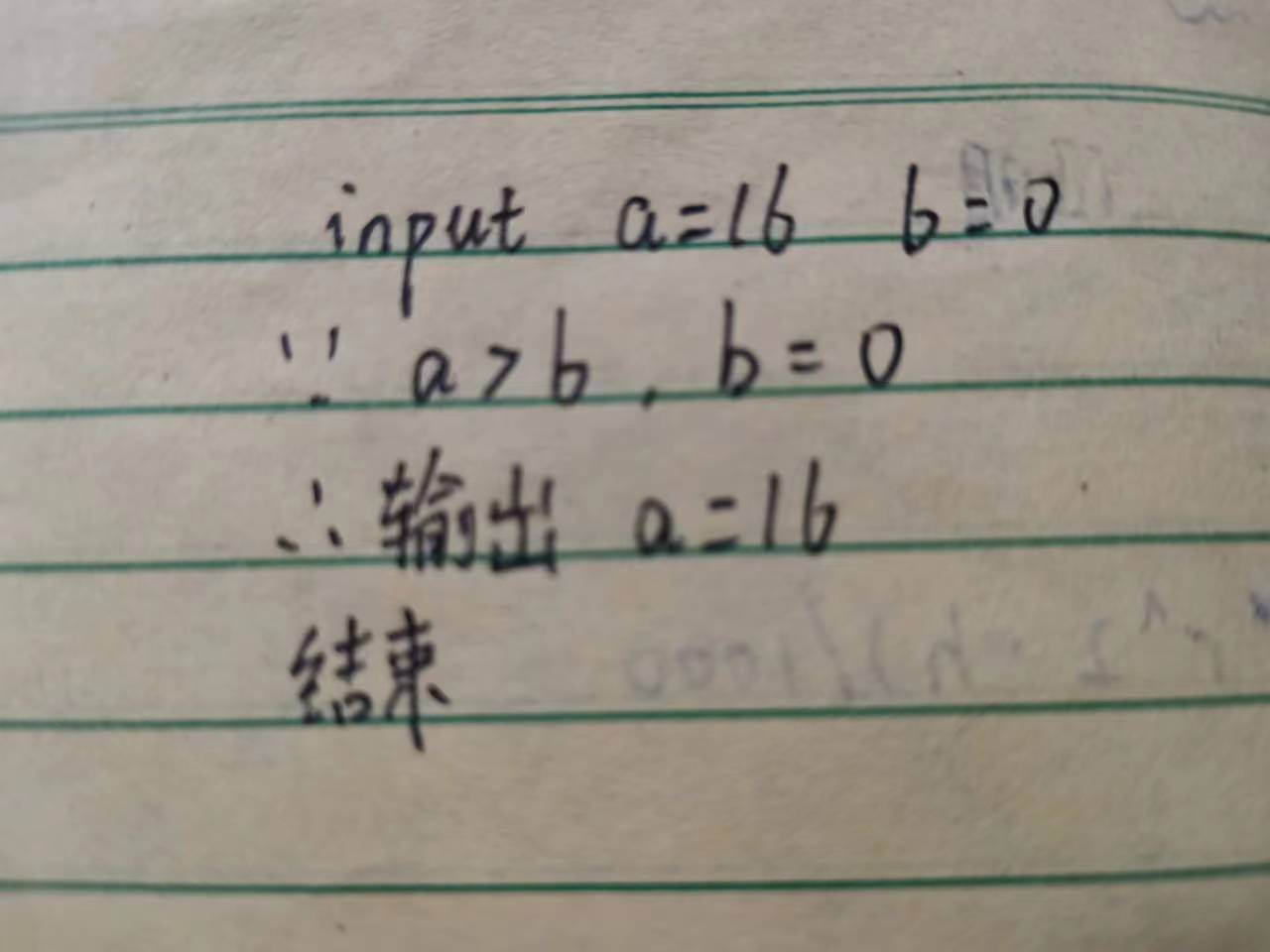
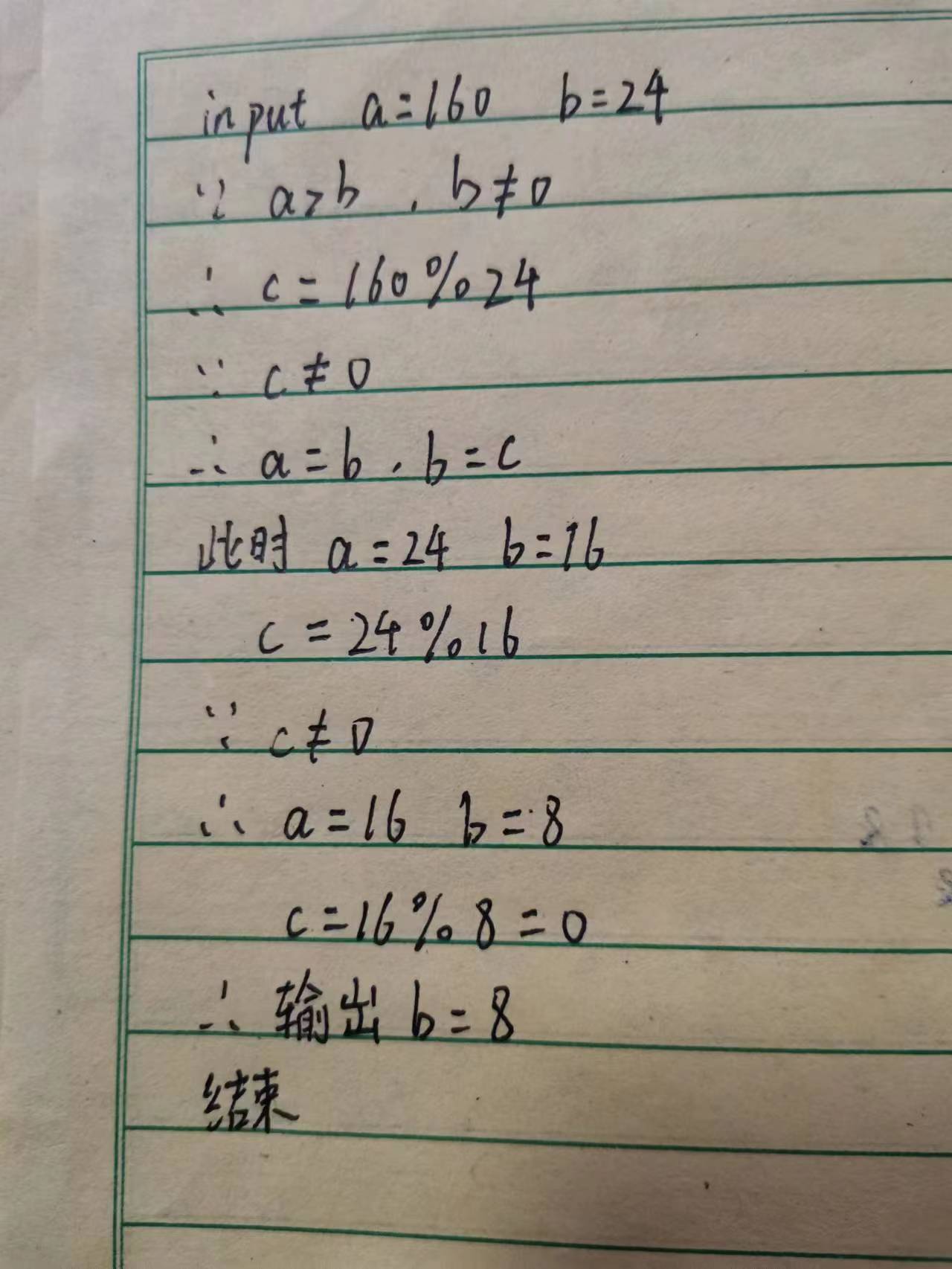



 浙公网安备 33010602011771号
浙公网安备 33010602011771号