常见插值算法--拉格朗日插值、三次卷积插值、三次样条插值、兰克索斯插值
写在前面
本文简单介绍了几种常见的插值算法并附带了相应的python代码,本文公式使用latex编写,如有错误欢迎评论指出,如果谁知道如何修改latex字号也欢迎留言
关于一维、二维和多维插值
三次卷积插值、拉格朗日两点插值(线性插值)、兰克索斯插值在二维插值时改变x和y方向的计算顺序不影响最终结果,这三个也是图像缩放插值时常用的插值算法,而其他插值在改变计算顺序时会产生明显差异,多维的情况笔者没有尝试,读者可以自行尝试或推导
在待求像素的四邻像素中,将距离待求像素最近的像素值赋给待求像素
$p_{11}$ $p_{12}$
$p$
$p_{21}$ $p_{22}$
python代码
1 def NN_interpolation(srcImg, dstH, dstW): 2 scrH, scrW, _ = srcImg.shape 3 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8) 4 for i in range(dstH - 1): 5 for j in range(dstW - 1): 6 scrX = round(i * (scrH / dstH)) 7 scrY = round(j * (scrW / dstW)) 8 dstImg[i, j] = srcImg[scrX, scrY] 9 return dstImg
拉格朗日插值(Lagrange Interpolation)
$拉格朗日插值法需要找到k个p_i(x)函数,使得每个函数分别在在x_i处取值为1,其余点取值为0,则y_ip_i(x)可以保证在x_i处取值为y_i,在其余点取值为0,因此L_k(x)能恰好经过所有点,这样的多项式被称为拉格朗日插值多项式,记为$
$L_k(x)=\sum_{i=1}^ky_ip_i(x)$
$p_i(x)=\prod_{j \neq i}^{1 \leq j \leq k}\frac{x-x_j}{x_i-x_j}$
$以四点即三次图像插值为例,因为横坐标间隔为1,则设四个点横坐标为-1、0、1和2,可得p_1(x)、p_2(x)、p_3(x)和p_4(x)$
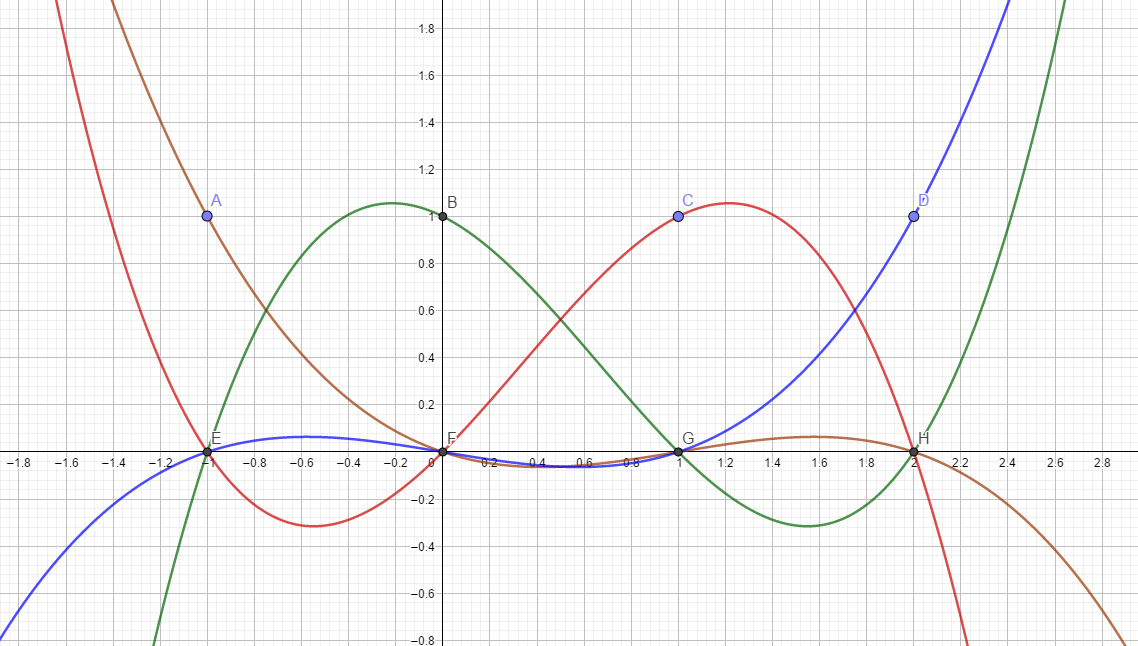
$假设y_1、y_2、y_3和y_4分别为1、2、-1、4,则可得拉格朗日函数如下图所示,待插值点横坐标范围为[0,1]$
在K=2时
在k=2时,也被称为线性插值
通用公式
$p_1=\frac{x-x_2}{x_1-x_2}$
$p_2=\frac{x-x_1}{x_2-x_1}$
\begin{align}
L_2x &= p_1y_1+p_2y_2 \nonumber \\
&= \frac{x-x_2}{x_1-x_2}y_1 + \frac{x-x_1}{x_2-x_1}y_2 \nonumber
\end{align}
图像插值
像素分布如图所示
$p_{11}$ $p_{12}$
$p$
$p_{21}$ $p_{22}$
$即当x_{i+1}=x_i+1时,设p与p_{11}的横纵坐标差分别为dx和dy$
\begin{align}
L_2x &= \frac{x-x_2}{x_1-x_2}y_1 + \frac{x-x_1}{x_2-x_1}y_2 \nonumber \\
&= (x_2-x)y_1+(x-x_1)y_2 \nonumber \\
&= (1-dx)y_1+dxy_2 \nonumber \\
&= (y_2-y_1)dx+y_1 \nonumber
\end{align}
$L_2'x=y_2-y_1$
在K=3时
通用公式
$p_1=\frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}$
$p_2=\frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}$
$p_3=\frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}$
\begin{align}
L_3x &= p_1y_1+p_2y_2+p_3y_3 \nonumber \\
&= \frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}y_1+\frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}y_2+\frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}y_3 \nonumber
\end{align}
图像插值
像素分布如图所示
$p_{11}$ $p_{12}$ $p_{13}$
$p_{21}$ $p_{22}$ $p_{23}$
$p$
$p_{31}$ $p_{32}$ $p_{33}$
$即当x_{i+1}=x_i+1时,设p与p_{11}的横纵坐标差分别为dx和dy$
\begin{align}
L_3x &= \frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}y_1 + \frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}y_2 + \frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}y_3 \nonumber \\
&= \frac{-dx(1-dx)}{(-1)\cdot(-2)}y_1 + \frac{-(1+dx)(1-dx)}{1\cdot(-1)}y_2 + \frac{(1+dx)dx}{2\cdot 1}y_3 \nonumber \\
&= (\frac{1}{2}d^2x-\frac{1}{2}dx)y_1 - (d^2x-1)y_2 + (\frac{1}{2}d^2x+\frac{1}{2}dx)y_3 \nonumber \\
&= d^2x(\frac{1}{2}y_1-y_2+\frac{1}{2}y_3)+dx(-\frac{1}{2}y_1+\frac{1}{2}y_3)+y_2 \nonumber
\end{align}
$L_3'x=dx(y_1-2y_2+y_3)+(\frac{1}{2}y_3-\frac{1}{2}y_1)$
在K=4时
通用公式
$p_1=\frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}\frac{x-x_4}{x_1-x_4}$
$p_2=\frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}\frac{x-x_4}{x_2-x_4}$
$p_3=\frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}\frac{x-x_4}{x_3-x_4}$
$p_4=\frac{x-x_1}{x_4-x_1}\frac{x-x_2}{x_4-x_2}\frac{x-x_3}{x_4-x_3}$
\begin{align}
L_4x &= p_1y_1+p_2y_2+p_3y_3+p_4y_4 \nonumber \\
&= \frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}\frac{x-x_4}{x_1-x_4}y_1 + \frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}\frac{x-x_4}{x_2-x_4}y_2 + \frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}\frac{x-x_4}{x_3-x_4}y_3 + \frac{x-x_1}{x_4-x_1}\frac{x-x_2}{x_4-x_2}\frac{x-x_3}{x_4-x_3}y_4 \nonumber
\end{align}
图像插值
$p_{11}$ $p_{12}$ $p_{13}$ $p_{14}$
$p_{21}$ $p_{22}$ $p_{23}$ $p_{24}$
$p$
$p_{31}$ $p_{32}$ $p_{33}$ $p_{34}$
$p_{41}$ $p_{42}$ $p_{43}$ $p_{44}$
$即当x_{i+1}=x_i+1时,设p与p_{11}的横纵坐标差分别为dx和dy$
\begin{align}
L_4x &= \frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}\frac{x-x_4}{x_1-x_4}y_1
+ \frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}\frac{x-x_4}{x_2-x_4}y_2
+ \frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}\frac{x-x_4}{x_3-x_4}y_3
+ \frac{x-x_1}{x_4-x_1}\frac{x-x_2}{x_4-x_2}\frac{x-x_3}{x_4-x_3}y_4 \nonumber \\
&= \frac{dx[-(1-dx)][-(2-dx)]}{(-1)\cdot(-2)\cdot(-3)}y_1
+ \frac{(1+dx)[-(1-dx)][-(2-dx)]}{1\cdot(-1)\cdot(-2)}y_2
+ \frac{(1+dx)dx[-(2-dx)]}{2\cdot 1\cdot(-1)}y_3
+ \frac{(1+dx)dx[-(1-dx)]}{3\cdot 2\cdot 1}y_4 \nonumber \\
&= \frac{d^3x-3d^2x+2dx}{-6}y1 + \frac{d^3x-2d^2x-dx+2}{2}y_2 + \frac{d^3x-d^2x-2dx}{-2}y_3 + \frac{d^3x-dx}{6}y_4 \nonumber \\
&= d^3x(-\frac{1}{6}y_1+\frac{1}{2}y_2-\frac{1}{2}y_3+\frac{1}{6}y_4)+d^2x(\frac{1}{2}y_1-y_2+\frac{1}{2}y_3)+dx(-\frac{1}{3}y_1-\frac{1}{2}y_2+y_3-\frac{1}{6}y_4)+y_2 \nonumber
\end{align}
\begin{align}
L_4'x &= d^2x(-\frac{1}{2}y_1+\frac{3}{2}y_2-\frac{3}{2}y_3+\frac{1}{2}y_4)+dx(y_1-2y_2+y_3)+(-\frac{1}{3}y_1-\frac{1}{2}y_2+y_3-\frac{1}{6}y_4) \nonumber \\
&= -[\frac{1}{2}d^2x(y_1-3y_2+3y_3-y_4)-dx(y_1-2y_2+y_3)+\frac{1}{6}(2y_1+3y_2-6y_3+y_4)] \nonumber
\end{align}
python代码
插值核计算的时候乘法和加减法计算的顺序不同可能会导致结果存在细微的差异,读者可以自行研究一下
1 class BiLagrangeInterpolation: 2 @staticmethod 3 def LagrangeInterpolation2(x, y1, y2): 4 f1 = 1 - x 5 f2 = x 6 result = y1 * f1 + y2 * f2 7 return result 8 9 @staticmethod 10 def LagrangeInterpolation3(x, y1, y2, y3): 11 f1 = (x ** 2 - x) / 2.0 12 f2 = 1 - x ** 2 13 f3 = (x ** 2 + x) / 2.0 14 result = y1 * f1 + y2 * f2 + y3 * f3 15 return result 16 17 @staticmethod 18 def LagrangeInterpolation4(x, y1, y2, y3, y4): 19 f1 = - (x ** 3 - 3 * x ** 2 + 2 * x) / 6.0 20 f2 = (x ** 3 - 2 * x ** 2 - x + 2) / 2.0 21 f3 = - (x ** 3 - x ** 2 - 2 * x) / 2.0 22 f4 = (x ** 3 - x) / 6.0 23 result = y1 * f1 + y2 * f2 + y3 * f3 + y4 * f4 24 return result 25 26 def biLag2_2(self, srcImg, dstH, dstW): 27 dstH, dstW = int(dstH), int(dstW) 28 srcH, srcW, _ = srcImg.shape 29 srcImg = np.pad(srcImg, ((1, 1), (1, 1), (0, 0)), 'edge') 30 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8) 31 for dstY in range(dstH): 32 for dstX in range(dstW): 33 for channel in [0, 1, 2]: 34 # p11 p12 35 # p 36 # p21 p22 37 # 储存为 p(y, x) 38 p = [dstY * srcH / dstH, dstX * srcW / dstW] 39 p11 = [math.floor(p[0]), math.floor(p[1])] 40 p12 = [p11[0], p11[1] + 1] 41 42 p21 = [p11[0] + 1, p11[1]] 43 p22 = [p21[0], p12[1]] 44 45 diff_y, diff_x = p[0] - p11[0], p[1] - p11[1] 46 r1 = self.LagrangeInterpolation2(diff_x, srcImg[p11[0], p11[1], channel], srcImg[p12[0], p12[1], channel]) 47 r2 = self.LagrangeInterpolation2(diff_x, srcImg[p21[0], p21[1], channel], srcImg[p22[0], p22[1], channel]) 48 49 c = self.LagrangeInterpolation2(diff_y, r1, r2) 50 51 dstImg[dstY, dstX, channel] = np.clip(c, 0, 255) 52 return dstImg 53 54 def biLag3_3(self, srcImg, dstH, dstW): 55 dstH, dstW = int(dstH), int(dstW) 56 srcH, srcW, _ = srcImg.shape 57 srcImg = np.pad(srcImg, ((1, 1), (1, 1), (0, 0)), 'edge') 58 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8) 59 for dstY in range(dstH): 60 for dstX in range(dstW): 61 for channel in [0, 1, 2]: 62 # p11 p12 p13 63 # 64 # p21 p22 p23 65 # p 66 # p31 p32 p33 67 # 储存为 p(y, x) 68 p = [dstY * srcH / dstH, dstX * srcW / dstW] 69 p22 = [math.floor(p[0]), math.floor(p[1])] 70 p21 = [p22[0], p22[1] - 1] 71 p23 = [p22[0], p22[1] + 1] 72 73 p11 = [p21[0] - 1, p21[1]] 74 p12 = [p11[0], p22[1]] 75 p13 = [p11[0], p23[1]] 76 77 p31 = [p21[0] + 1, p21[1]] 78 p32 = [p31[0], p22[1]] 79 p33 = [p31[0], p23[1]] 80 81 diff_y, diff_x = p[0] - p22[0], p[1] - p22[1] 82 r1 = self.LagrangeInterpolation3(diff_x, srcImg[p11[0], p11[1], channel], srcImg[p12[0], p12[1], channel], srcImg[p13[0], p13[1], channel]) 83 r2 = self.LagrangeInterpolation3(diff_x, srcImg[p21[0], p21[1], channel], srcImg[p22[0], p22[1], channel], srcImg[p23[0], p23[1], channel]) 84 r3 = self.LagrangeInterpolation3(diff_x, srcImg[p31[0], p31[1], channel], srcImg[p32[0], p32[1], channel], srcImg[p33[0], p33[1], channel]) 85 86 c = self.LagrangeInterpolation3(diff_y, r1, r2, r3) 87 88 dstImg[dstY, dstX, channel] = np.clip(c, 0, 255) 89 return dstImg 90 91 def biLag4_4(self, srcImg, dstH, dstW): 92 dstH, dstW = int(dstH), int(dstW) 93 srcH, srcW, _ = srcImg.shape 94 srcImg = np.pad(srcImg, ((1, 2), (1, 2), (0, 0)), 'edge') 95 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8) 96 for dstY in range(dstH): 97 for dstX in range(dstW): 98 for channel in [0, 1, 2]: 99 # p11 p12 p13 p14 100 # 101 # p21 p22 p23 p24 102 # p 103 # p31 p32 p33 p34 104 # 105 # p41 p42 p43 p44 106 # 储存为 p(y, x) 107 p = [dstY * srcH / dstH, dstX * srcW / dstW] 108 p22 = [math.floor(p[0]), math.floor(p[1])] 109 p21 = [p22[0], p22[1] - 1] 110 p23 = [p22[0], p22[1] + 1] 111 p24 = [p22[0], p22[1] + 2] 112 113 p11 = [p21[0] - 1, p21[1]] 114 p12 = [p11[0], p22[1]] 115 p13 = [p11[0], p23[1]] 116 p14 = [p11[0], p24[1]] 117 118 p31 = [p21[0] + 1, p21[1]] 119 p32 = [p31[0], p22[1]] 120 p33 = [p31[0], p23[1]] 121 p34 = [p31[0], p24[1]] 122 123 p41 = [p21[0] + 2, p21[1]] 124 p42 = [p41[0], p22[1]] 125 p43 = [p41[0], p23[1]] 126 p44 = [p41[0], p24[1]] 127 128 diff_y, diff_x = p[0] - p22[0], p[1] - p22[1] 129 r1 = self.LagrangeInterpolation4(diff_x, srcImg[p11[0], p11[1], channel], srcImg[p12[0], p12[1], channel], srcImg[p13[0], p13[1], channel], srcImg[p14[0], p14[1], channel]) 130 r2 = self.LagrangeInterpolation4(diff_x, srcImg[p21[0], p21[1], channel], srcImg[p22[0], p22[1], channel], srcImg[p23[0], p23[1], channel], srcImg[p24[0], p24[1], channel]) 131 r3 = self.LagrangeInterpolation4(diff_x, srcImg[p31[0], p31[1], channel], srcImg[p32[0], p32[1], channel], srcImg[p33[0], p33[1], channel], srcImg[p34[0], p34[1], channel]) 132 r4 = self.LagrangeInterpolation4(diff_x, srcImg[p41[0], p41[1], channel], srcImg[p42[0], p42[1], channel], srcImg[p43[0], p43[1], channel], srcImg[p44[0], p44[1], channel]) 133 134 c = self.LagrangeInterpolation4(diff_y, r1, r2, r3, r4) 135 136 dstImg[dstY, dstX, channel] = np.clip(c, 0, 255) 137 return dstImg
三次卷积插值法(Cubic Convolution Interpolation)

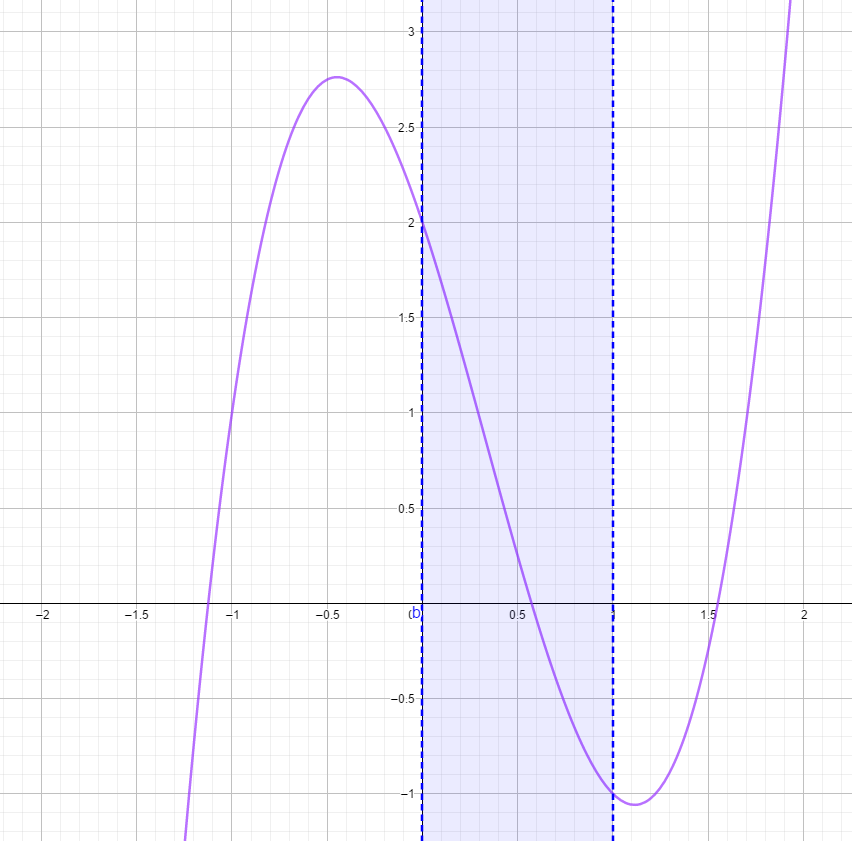
$使用上图中的卷积核进行加权平均计算,卷积核为u(s),四个等距(距离为1)的采样点记为x_0、x_1、x_2和x_3,采样数值记为y_0、y_1、y_2和y_3,且保证四个点均在[-2,2]区间上,计算得到g(x),假设y_1、y_2、y_3和y_4分别为1、2、-1、4,则可得三次卷积插值函数如下图所示,待插值点横坐标范围为[0,1]$

公式推导
$设u(s)=\begin{cases} A_1|s|^3+B_1|s|^2+C_1|s|+D_1, &0<|s|<1 \\ A_2|s|^3+B_2|s|^2+C_2|s|+D_2, &1<|s|<2 \\ 1, &s=0 \\ 0, &otherwise \end{cases}$
$\because函数在s=0,1,2处连续$
$\therefore\begin{cases} 1=u(0^+)=D_1 \\ 0=u(1^-)=A_1+B_1+C_1+D_1 \\ 0=u(1^+)=A_2+B_2+C_2+D_2 \\ 0=u(2^-)=8A_2+4B_2+2C_2+D_2 \end{cases} (1)$
$\because函数在s=0,1,2处导函数连续$
$\therefore\begin{cases} u'(0^-)=u'(0+) \\ u'(1^-)=u'(1+) \\ u'(2^-)=u'(2+)\end{cases} \Rightarrow \begin{cases} -C_1=C_1 \\ 3A_1+2B_1+C_1=3A_2+2B_2+C_2 \\ 12A_2+4B_2+C+2=0 \end{cases} ~~~~ (2)$
$联立方程组(1)(2),设A_2=a,解得$
$\begin{cases} A_1=a+2 \\ B_1=-(a+3) \\ C_1=0 \\ D_1=1 \\ A_2=a \\ B_2=-5a \\ C_2=8a \\ D_2=-4a \end{cases}\Rightarrow u(s)=\begin{cases} (a+2)|s|^3-(a+3)|s|^2+1, &0<|s|<1 \\ A_2|s|^3+B_2|s|^2+C_2|s|+D_2, &1<|s|<2\\ 1, &s=0 \\ 0, &otherwise \end{cases}$
$\because g(x)=\sum_kC_ku(s+j-k), ~~~~k=j-1,j, j+1,j+2且0<s<1$
$又\because \begin{cases}\begin{align} u(s+1)&=as^3-2as^2+as \nonumber \\ u(s)&=(a+2)s^3-(a+3)s^2+1 \nonumber \\ u(s-1)&=-(a+2)s^3+(2a+3)s^2-as \nonumber \\ u(s-2)&=-as^3+as^2 \nonumber \end{align}\end{cases}$
$\begin{align} \therefore g(x) &= C_{j-1}u(s+1)+C_{j}u(s)+C_{j+1}u(s-1)+C_{j+2}u(s-2) \nonumber \\ &= C_{j-1}(as^3-2as^2+as)+C_j[(a+2)s^3-(a+3)s^2+1]+C_{j+1}[-(a+2)s^3+(2a+3)s^2-as]+C_{j+2}[-a^3+as^2] \nonumber \\ &= s^3[aC_{j-1}+(a+2)C_j-(a+2)C_{j+1}-aC_{j+2}]+s^2[-2aC_{j-1}-(a+3)C_j+(2a+3)C_{j+1}+aC_{j+2}]+s[aC_{j-1}-aC_{j+1}]+C_j \nonumber \end{align} ~~(3)$
$f在x_j处泰勒展开得到$
$f(x)=f(x_j)+f'(x_j)(x-x_j)+\frac{1}{2}f''(x_j)(x-x_j)^2+\cdots$
$\therefore \begin{cases} f(x_{j+1})=f(x_j)+f'(x_j)(x_{j+1}-x_j)+\frac{1}{2}f''(x_j)(x_{j+1}-x_j)^2+\cdots \\ f(x_{j+2})=f(x_j)+f'(x_j)(x_{j+2}-x_j)+\frac{1}{2}f''(x_j)(x_{j+2}-x_j)^2+\cdots \\ f(x_{j-1})=f(x_j)+f'(x_j)(x_{j-1}-x_j)+\frac{1}{2}f''(x_j)(x_{j-1}-x_j)^2+\cdots \end{cases}$
$令x_{j+1}-x_j=h$
$\because x_{i+1}=x_i+1$
$\therefore x_{j+2}-x_j=2h,x_{j-1}-x_j=-h$
$\therefore \begin{cases} f(x_{j+2})=f(x_j)+2f'(x_j)h+2f''(x_j)h^2+\cdots \\ f(x_{j+1})=f(x_j)+f'(x_j)h+\frac{1}{2}f''(x_j)h^2+\cdots \\ f(x_{j-1})=f(x_j)-f'(x_j)h+\frac{1}{2}f''(x_j)h^2+\cdots \end{cases}$
$\therefore \begin{cases} c_{j-1}=f(x_j)-f'(x_j)h+\frac{1}{2}f''(x_j)h^2+o(h^3) \\ c_j=f(x_j) \\ c_{j+1}=f(x_j)+f'(x_j)h+\frac{1}{2}f''(x_j)h^2+o(h^3) \\ c_{j+2}=f(x_j)+2f'(x_j)h+2f''(x_j)h^2+o(h^3) \end{cases} ~~ (4) $
$将(4)代入(3),得$
$g(x)=-(2a+1)[2hf'(x_j)+h^2f''(x_j)]s^3+[(6a+3)hf'(x_j)+\frac{4a+3}{2}h^2f''(x_j)]s^2-2ahf'(x_j)s+f(x_j)+o(h^3)$
$\because h=1,s=x-x_J$
$\therefore sh=x-x_j$
$\begin{align}\therefore f(x)&= f(x_j)+f'(x_j)(x-x_j)+\frac{1}{2}f''(x_j)(x-x_j)^2+o(h^3) \nonumber \\ &= f(x_j)+f'(x_j)sh+\frac{1}{2}f''(x_j)s^2h^2+o(h^3) \nonumber \end{align}$
$\therefore f(x)-g(x)=(2a+1)[2hf'(x_j)+h^2f''(x_j)]s^3-(2a+1)[3hf'(x_j)+h^2f''(x_j)]s^2+[(2a+1)hf'(x_j)]s+o(h^3)$
$\because 期望f(x)-g(x)趋于0$
$\therefore 2a+1=0 \Rightarrow a=-\frac{1}{2}$
$\therefore u(s)=\begin{cases} \frac{3}{2}|s|^3-\frac{5}{2}|s|^2+1, &0<|s|<1 \\ -\frac{1}{2}|s|^3+\frac{5}{2}|s|^2-4|s|+2, &1<|s|<2 \\ 1, &s=0 \\ 0, &otherwise \end{cases}$
$\therefore g(s)=s^3[-\frac{1}{2}c_{j-1}+\frac{3}{2}c_j-\frac{3}{2}c_{j+1}+\frac{1}{2}c_{j+2}]+s^2[c_{j-1}-\frac{5}{2}c_j+2c_{j+1}-\frac{1}{2}c_{j+2}]+s[-\frac{1}{2}c_{j-1}+\frac{1}{2}c_{j+1}]+c_j$
图像插值
$p_{11}$ $p_{12}$ $p_{13}$ $p_{14}$
$p_{21}$ $p_{22}$ $p_{23}$ $p_{24}$
$p$
$p_{31}$ $p_{32}$ $p_{33}$ $p_{34}$
$p_{41}$ $p_{42}$ $p_{43}$ $p_{44}$
python代码
1 class BiCubicConvInterpolation: 2 @staticmethod 3 def CubicConvInterpolation1(p0, p1, p2, p3, s): 4 # 用g(s)公式计算,已经将四个u(s)计算完毕并整理 5 # as^3 + bs^2 + cs + d 6 a = 0.5 * (-p0 + 3.0 * p1 - 3.0 * p2 + p3) 7 b = 0.5 * (2.0 * p0 - 5.0 * p1 + 4.0 * p2 - p3) 8 c = 0.5 * (-p0 + p2) 9 d = p1 10 return d + s * (c + s * (b + s * a)) 11 12 @staticmethod 13 def CubicConvInterpolation2(s): 14 # 用u(s)公式计算 15 s = abs(s) 16 if s <= 1: 17 return 1.5 * s ** 3 - 2.5 * s ** 2 + 1 18 elif s <= 2: 19 return -0.5 * s ** 3 + 2.5 * s ** 2 - 4 * s + 2 20 else: 21 return 0 22 23 def biCubic1(self, srcImg, dstH, dstW): 24 # p11 p12 p13 p14 25 # 26 # p21 p22 p23 p24 27 # p 28 # p31 p32 p33 p34 29 # 30 # p41 p42 p43 p44 31 dstH, dstW = int(dstH), int(dstW) 32 scrH, scrW, _ = srcImg.shape 33 srcImg = np.pad(srcImg, ((1, 1), (1, 1), (0, 0)), 'edge') 34 dstImg = np.zeros((dstH, dstW, 1), dtype=np.uint8) 35 for dstY in range(dstH): 36 for dstX in range(dstW): 37 for channel in [0]: 38 y = dstY * scrH / dstH 39 x = dstX * scrW / dstW 40 y1 = math.floor(y) 41 x1 = math.floor(x) 42 43 array = [] 44 for i in [-1, 0, 1, 2]: 45 temp = self.CubicConvInterpolation1(srcImg[y1 + i, x1 - 1, channel], 46 srcImg[y1 + i, x1, channel], 47 srcImg[y1 + i, x1 + 1, channel], 48 srcImg[y1 + i, x1 + 2, channel], 49 x - x1) 50 array.append(temp) 51 52 temp = self.CubicConvInterpolation1(array[0], array[1], array[2], array[3], y - y1) 53 dstImg[dstY, dstX, channel] = np.clip(temp, 0, 255) 54 55 return dstImg 56 57 def biCubic2(self, srcImg, dstH, dstW): 58 # p11 p12 p13 p14 59 # 60 # p21 p22 p23 p24 61 # p 62 # p31 p32 p33 p34 63 # 64 # p41 p42 p43 p44 65 dstH, dstW = int(dstH), int(dstW) 66 scrH, scrW, _ = srcImg.shape 67 srcImg = np.pad(srcImg, ((1, 1), (1, 1), (0, 0)), 'edge') 68 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8) 69 for dstY in range(dstH): 70 for dstX in range(dstW): 71 for channel in [0, 1, 2]: 72 y = dstY * scrH / dstH 73 x = dstX * scrW / dstW 74 y1 = math.floor(y) 75 x1 = math.floor(x) 76 77 array = [] 78 for i in [-1, 0, 1, 2]: 79 temp = 0 80 for j in [-1, 0, 1, 2]: 81 temp += srcImg[y1 + i, x1 + j, channel] * self.CubicConvInterpolation2(x - (x1 + j)) 82 array.append(temp) 83 84 temp = 0 85 for i in [-1, 0, 1, 2]: 86 temp += array[i + 1] * self.CubicConvInterpolation2(y - (y1 + i)) 87 dstImg[dstY, dstX, channel] = np.clip(temp, 0, 255) 88 89 return dstImg
三次样条插值
$在n-1个区间上寻找n-1个三次曲线,使其满足相邻曲线在端点处值相等、一阶导数相等,二阶导数相等,在加以边界条件后可得每个曲线的方程,然后沿x轴依次偏移对应的距离即可得到插值结果,如仅需要特定范围内的结果,则可以大幅减少计算量$
公式推导
$设S_i(x)=a_i+b_i(x-x_i)+c_i(x-x_i)^2+d_i(x-x_i)^3, ~~~~i=0,1,...,n-1$
$则 \begin{cases} S_i'(x)=b_i+2c_i(x-x_i)+3d_i(x-x_i)^2\\ S_i''(x)=2c_i+6d_i(x-x_i)\\ S_i'''(x)=6d_i\\ \end{cases} ~~~~i=0,1,...,n-1$
$设h_i(x)=x_{i+1}-x_i,可得$
$\begin{cases} S_i(x)=a_i+b_ih_i+c_ih_i^2+d_ih_i^3\\ S_i'(x)=b_i+2c_ih_i+3d_ih_i^2\\ S_i''(x)=2c_i+6d_ih_i\\ S_i'''(x)=6d_i\\ \end{cases} ~~~~i=0,1,...,n-1$
$\because S_i(x)过点(x_i,y_i)$
$\therefore S_i(x)=a_i=y+i, ~~~~i=0,1,...,n-1 ~~~~~~(1)$
$\because S_i(x)与S_{i+1}(x)在X_{i+1}处相等$
$\therefore S_i(x_{i+1})=S_{i+1}(x_{i+1})$
$\Rightarrow a_i+b_ih_i+c_ih_i^2+d_ih_i^3=y_{i+1}, ~~~~i=0,1,...,n-2~~~~~~(2)$
$\because S_i'(x)与S_{i+1}'(x)在X_{i+1}处相等$
$\therefore S_i'(x)-S_{i+1}'(x)=0$
$\Rightarrow b_i+2c_ih_i+3d_ih_i^2-b_{i+1}=0~~~~~~(3)$
$\because S_i''(x)与S_{i+1}''(x)在X_{i+1}处相等$
$\therefore S_i''(x)-S_{i+1}''(x)=0$
$\Rightarrow 2c_i+6d_ih_i-2c_{i+1}=0, ~~~~i=0,1,...,n-2~~~~~~(4)$
$设m_i=S_i(x_i)=2c_i,即c_i=\frac{1}{2}m_i, ~~~~i=0,1,...,n-1~~~~~~(5)$
$将(5)代入(4),得$
$2c_i+6d_ih_i-2c_{i+1}=0$
$\Rightarrow m_i+6h_id_i-m_{i+1}=0$
$\Rightarrow d_i=\frac{m_{i+1}-m_i}{6h_i}, ~~~~i=0,1,...,n-2~~~~~~(6)$
$将(1)(5)(6)代入(2),得$
\begin{align}
&a_i+b_ih_i+c_ih_i^2+d_ih_i^3=y_{i+1} \nonumber \\
\Rightarrow&y_i+b_ih_i+\frac{1}{2}m_ih_i^2+\frac{m_{i+1}-m_i}{6h_i}h_i^3=y_{i+1} \nonumber \\
\Rightarrow&b_i=\frac{y_{i+1}-y_i}{h_i}-\frac{1}{2}m_ih_i-\frac{1}{6}(m_{i+1}-m_i)h_i \nonumber \\
\Rightarrow&b_i=\frac{y_{i+1}-y_i}{h_i}-\frac{1}{3}m_ih_i-\frac{1}{6}m_{i+1}h_i, ~~~~i=0,1,...,n-2~~~~~~(7) \nonumber
\end{align}
$将(5)(6)(7)代入(3),得$
\begin{align}
&\frac{y_{i+1}-y{i}}{h_i}-\frac{1}{3}m_ih_i-\frac{1}{6}m_{i+1}h_i+2\cdot\frac{1}{2}m_ih_i+3\frac{m_{i+1}-m_i}{6h_i}h_i^2-(\frac{y_{i+2}-y_{i+1}}{h_{i+1}}-\frac{1}{3}m_{i+1}h_{i+1}-\frac{1}{6}m_{i+2}h_{i+1})=0 \nonumber \\
\Rightarrow&\frac{y_{i+1}-y{i}}{h_i}-\frac{1}{3}m_ih_i-\frac{1}{6}m_{i+1}h_i+m_ih_i+\frac{1}{2}(m_{i+1}-m_i)h_i-\frac{y_{i+2}-y_{i+1}}{h_{i+1}}+\frac{1}{3}m_{i+1}h_{i+1}+\frac{1}{6}m_{i+2}h_{i+1}=0 \nonumber \\
\Rightarrow&m_ih_i(-\frac{1}{3}+1-\frac{1}{2})+m_{i+1}h_i(-\frac{1}{6}+\frac{1}{2})+\frac{1}{3}m_{i+1}h_{i+1}+\frac{1}{6}m_{i+2}h_{i+1}=\frac{y_{i+2}-y_{i+1}}{h_{i+1}}-\frac{y_{i+1}-y_{i}}{h_{i}} \nonumber \\
\Rightarrow&\frac{1}{6}(m_ih_i+2m_{i+1}h_i+2m_{i+1}h_{i+1}+m_{i+2}h_{i+1})=\frac{y_{i+2}-y_{i+1}}{h_{i+1}}-\frac{y_{i+1}-y_{i}}{h_{i}} \nonumber \\
\Rightarrow&m_ih_i+2m_{i+1}(h_i+h_{i+1})+m_{i+2}h_{i+1}=6(\frac{y_{i+2}-y_{i+1}}{h_{i+1}}-\frac{y_{i+1}-y_{i}}{h_{i}}), ~~~~i=0,1,...,n-2~~~~~~(8) \nonumber
\end{align}
$由(8)可知i=0,1,...,n-2,则有m_0,m_1,...,m_n,需要两个额外条件方程组才有解$
自然边界(Natural)
$m_0=0,m_n=0$
\begin{bmatrix} \tiny
1 & 0 & 0 & 0 & 0 & \cdots & 0\\
h_0 & 2(h_0+h_1) & h_1 & 0 & 0 & \cdots & 0\\
0 & h_1 & 2(h_1+h_2) & h_2 & 0 & \cdots & 0\\
0 & 0 & h_2 & 2(h_2+h_3) & h_3 & \cdots & 0\\
\vdots& & & \ddots & \ddots & \ddots & \vdots\\
0 & \cdots & & & h_{n-2} & 2(h_{n-2}+h_{n-1}) & h_{n-1}\\
0 & \cdots & & & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
m_0\\m_1\\m_2\\m_3\\\vdots\\m_{n-1}\\m_n
\end{bmatrix}=6
\begin{bmatrix}
0\\
\frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\
\frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\
\frac{y_4-y_3}{h_3}-\frac{y_3-y_2}{h_2}\\
\vdots\\
\frac{y_n-y_{n-1}}{h_{n-1}}-\frac{y_{n-1}-y_{n-2}}{h_{n-2}}\\
0
\end{bmatrix}
固定边界(Clamped)
\begin{align}
&\begin{cases}
S_0'(x_0)=A\\
S_{n-1}'(x_n)=B
\end{cases} \nonumber \\
\Rightarrow&\begin{cases}
b_0=A\\
b_{n-1}+2c_{n-1}h_{n-1}+3d_{n-1}h_{n-1}^2=B
\end{cases} \nonumber \\
\Rightarrow&\begin{cases}
A=\frac{y_1-y_0}{h_0}-\frac{h_0}{2}m_0-\frac{h_0}{6}(m_1-m_0)\\
B=\frac{y_n-y_{n-1}}{h_{n-1}}-\frac{1}{3}m_{n-1}h_{n-1}+m_{n-1}h_{n-1}+\frac{1}{2}m_nh_{n-1}-\frac{1}{2}m_{n-1}h_{n-1}
\end{cases} \nonumber \\
\Rightarrow&\begin{cases}
2h_0m_0+h_0m_1=6(\frac{y_1-y_0}{h_0}-A)\\
h_{n-1}m_{n-1}+2h_{n-1}m_{n}=6(B-\frac{y_n-y_{n-1}}{h_{n-1}})
\end{cases} \nonumber \\
\end{align}
\begin{bmatrix}
2 & 1 & 0 & 0 & 0 & \cdots & 0\\
h_0 & 2(h_0+h_1) & h_1 & 0 & 0 & \cdots & 0\\
0 & h_1 & 2(h_1+h_2) & h_2 & 0 & \cdots & 0\\
0 & 0 & h_2 & 2(h_2+h_3) & h_3 & \cdots & 0\\
\vdots& & & \ddots & \ddots & \ddots & \vdots\\
0 & \cdots & & & h_{n-2} & 2(h_{n-2}+h_{n-1}) & h_{n-1}\\
0 & \cdots & & & 0 & 1 & 2
\end{bmatrix}
\begin{bmatrix}
m_0\\m_1\\m_2\\m_3\\\vdots\\m_{n-1}\\m_n
\end{bmatrix}=6
\begin{bmatrix}
\frac{y_1-y_0}{h_0}-A\\
\frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\
\frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\
\frac{y_4-y_3}{h_3}-\frac{y_3-y_2}{h_2}\\
\vdots\\
\frac{y_n-y_{n-1}}{h_{n-1}}-\frac{y_{n-1}-y_{n-2}}{h_{n-2}}\\
B-\frac{y_n-y_{n-1}}{h_{n-1}}
\end{bmatrix}
非节点边界(Not-A-Knot)
\begin{align}
&\begin{cases}
S_0'''(x_1)=S_1'''(x_1)\\
S_{n-2}'''(x_{n-1})=S_{n-1}'''(x_{n-1})
\end{cases} \nonumber \\
\Rightarrow&\begin{cases}
6\cdot\frac{m_1-m_0}{6h_0}=6\cdot\frac{m_2-m_1}{6h_1}\\
6\cdot\frac{m_{n-1}-m_{n-2}}{6h_{n-2}}=6\cdot\frac{m_n-m_{n-1}}{6h_{n-1}}
\end{cases} \nonumber \\
\Rightarrow&\begin{cases}
h_1(m_1-m_0)=h_0(m_2-m_1)\\
h_{n-1}(m_{n-1}-m_{n-2})=h_{n-2}(m_n-m_{n-1})
\end{cases} \nonumber \\
\Rightarrow&\begin{cases}
-h_1m_0+(h_1+h_0)m_1-h_0m_2=0\\
-h_{n-1}m_{n-2}+(h_{n-1}+h_{n-2})m_{n-1}-h_{n-2}m_n=0
\end{cases} \nonumber \\
\end{align}
\begin{bmatrix}
-h_1 & h_0+h_1 & -h_0 & 0 & 0 & \cdots & 0\\
h_0 & 2(h_0+h_1) & h_1 & 0 & 0 & \cdots & 0\\
0 & h_1 & 2(h_1+h_2) & h_2 & 0 & \cdots & 0\\
0 & 0 & h_2 & 2(h_2+h_3) & h_3 & \cdots & 0\\
\vdots& & & \ddots & \ddots & \ddots & \vdots\\
0 & \cdots & & & h_{n-2} & 2(h_{n-2}+h_{n-1}) & h_{n-1}\\
0 & \cdots & & & -h_{n-1} & h_{n-1}+h_{n-2} & -h_{n-2}
\end{bmatrix}
\begin{bmatrix}
m_0\\m_1\\m_2\\m_3\\\vdots\\m_{n-1}\\m_n
\end{bmatrix}=6
\begin{bmatrix}
0\\
\frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\
\frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\
\frac{y_4-y_3}{h_3}-\frac{y_3-y_2}{h_2}\\
\vdots\\
\frac{y_n-y_{n-1}}{h_{n-1}}-\frac{y_{n-1}-y_{n-2}}{h_{n-2}}\\
0
\end{bmatrix}
在n=4时
通用公式
自然边界
\begin{bmatrix}
1 & 0 & 0 & 0 \\
h_0 & 2(h_0+h_1) & h_1 & 0 \\
0 & h_1 & 2(h_1+h_2) & h_2 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
m_0\\m_1\\m_2\\m_3
\end{bmatrix}=6
\begin{bmatrix}
0\\
\frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\
\frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\
0
\end{bmatrix}
固定边界
\begin{bmatrix}
2 & 1 & 0 & 0 \\
h_0 & 2(h_0+h_1) & h_1 & 0 \\
0 & h_1 & 2(h_1+h_2) & h_2 \\
0 & 0 & 1 & 2 \\
\end{bmatrix}
\begin{bmatrix}
m_0\\m_1\\m_2\\m_3
\end{bmatrix}=6
\begin{bmatrix}
\frac{y_1-y_0}{h_0}-A\\
\frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\
\frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\
B-\frac{y_3-y_2}{h_2}
\end{bmatrix}
非节点边界
\begin{bmatrix}
-h_1 & h_0+h_1 & -h_0 & 0 \\
h_0 & 2(h_0+h_1) & h_1 & 0 \\
0 & h_1 & 2(h_1+h_2) & h_2 \\
0 & -h_2 & h_1+h_2 & -h_1 \\
\end{bmatrix}
\begin{bmatrix}
m_0\\m_1\\m_2\\m_3
\end{bmatrix}=6
\begin{bmatrix}
0\\
\frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\
\frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\
0
\end{bmatrix}
图像插值
$x_{i+1}-x_i=1 \Rightarrow h_i(x)=1$
$在n=4时,即四个点时如下所示$
$p_{11}$ $p_{12}$ $p_{13}$ $p_{14}$
$p_{21}$ $p_{22}$ $p_{23}$ $p_{24}$
$p$
$p_{31}$ $p_{32}$ $p_{33}$ $p_{34}$
$p_{41}$ $p_{42}$ $p_{43}$ $p_{44}$
自然边界(可用TDMA或化简计算)
\begin{bmatrix}
1 & 0 & 0 & 0 \\
1 & 4 & 1 & 0 \\
0 & 1 & 4 & 1 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
m_0\\m_1\\m_2\\m_3
\end{bmatrix}=6
\begin{bmatrix}
0\\
y_0+y_2-2y_1\\
y_1+y_3-2y_2\\
0
\end{bmatrix}
固定边界(只能用TDMA计算)
\begin{bmatrix}
2 & 1 & 0 & 0 \\
1 & 4 & 1 & 0 \\
0 & 1 & 4 & 1 \\
0 & 0 & 1 & 2 \\
\end{bmatrix}
\begin{bmatrix}
m_0\\m_1\\m_2\\m_3
\end{bmatrix}=6
\begin{bmatrix}
y_1-y_0-A\\
y_0+y_2-2y_1\\
y_1+y_3-2y_2\\
y_2-y_3+B
\end{bmatrix}
非节点边界(只能化简计算)
\begin{bmatrix}
-1 & 2 & -1 & 0 \\
1 & 4 & 1 & 0 \\
0 & 1 & 4 & 1 \\
0 & -1 & 2 & -1 \\
\end{bmatrix}
\begin{bmatrix}
m_0\\m_1\\m_2\\m_3
\end{bmatrix}=6
\begin{bmatrix}
0\\
y_0+y_2-2y_1\\
y_1+y_3-2y_2\\
0
\end{bmatrix}
python代码
1 class BiSplineInterpolation: 2 @staticmethod 3 def TDMA(a, b, c, d): 4 n = len(d) 5 6 c[0] = c[0] / b[0] 7 d[0] = d[0] / b[0] 8 9 for i in range(1, n): 10 coef = 1.0 / (b[i] - a[i] * c[i - 1]) 11 c[i] = coef * c[i] 12 d[i] = coef * (d[i] - a[i] * d[i - 1]) 13 14 for i in range(n - 2, -1, -1): 15 d[i] = d[i] - c[i] * d[i + 1] 16 17 return d 18 19 @staticmethod 20 def Simplified_Natural4(y1, y2, y3, y4): 21 # 四点自然边界化简公式 22 d1 = y1 + y3 - 2 * y2 23 d2 = y2 + y4 - 2 * y3 24 25 k0 = 0 26 k1 = (4 * d1 - d2) * 0.4 27 k2 = (4 * d2 - d1) * 0.4 28 k3 = 0 29 30 return [k0, k1, k2, k3] 31 32 @staticmethod 33 def Simplified_Not_A_Knot4(y1, y2, y3, y4): 34 # 四点非节点边界化简公式 35 d1 = y1 + y3 - 2 * y2 36 d2 = y2 + y4 - 2 * y3 37 38 k0 = 2 * d1 - d2 39 k1 = d1 40 k2 = d2 41 k3 = 2 * d2 - d1 42 43 return [k0, k1, k2, k3] 44 45 # TDMA矩阵说明 46 # a0 和 c3 没有实际意义,占位用 47 # a0 [b0 c0 0 0 ] [x0] [d0] 48 # [a1 b1 c1 0 ] [x1] = [d1] 49 # [0 a2 b2 c2] [x2] [d2] 50 # [0 0 a3 b3] c3 [x3] [d3] 51 52 def SplineInterpolationNatural4(self, x, y1, y2, y3, y4): 53 # 用TDMA计算 54 # matrix_a = [0, 1, 1, 0] 55 # matrix_b = [1, 4, 4, 1] 56 # matrix_c = [0, 1, 1, 0] 57 # matrix_d = [0, 6 * (y1 + y3 - 2 * y2), 6 * (y2 + y4 - 2 * y3), 0] 58 # matrix_x = self.TDMA(matrix_a, matrix_b, matrix_c, matrix_d) 59 60 # 化简计算 61 matrix_x = self.Simplified_Natural4(y1, y2, y3, y4) 62 63 a = y2 64 b = y3 - y2 - matrix_x[1] / 3.0 - matrix_x[2] / 6.0 65 c = matrix_x[1] / 2.0 66 d = (matrix_x[2] - matrix_x[1]) / 6.0 67 68 s = a + b * x + c * x * x + d * x * x * x 69 return s 70 71 def SplineInterpolationClamped4(self, x, y1, y2, y3, y4): 72 # 仅有TDMA计算,无法化简 73 A, B = 1, 1 74 75 matrix_a = [0, 1, 1, 1] 76 matrix_b = [2, 4, 4, 2] 77 matrix_c = [1, 1, 1, 0] 78 matrix_d = [6 * (y2 - y1 - A), 6 * (y1 + y3 - 2 * y2), 6 * (y2 + y4 - 2 * y3), 6 * (B - y4 + y3)] 79 matrix_x = self.TDMA(matrix_a, matrix_b, matrix_c, matrix_d) 80 81 a = y2 82 b = y3 - y2 - matrix_x[1] / 3.0 - matrix_x[2] / 6.0 83 c = matrix_x[1] / 2.0 84 d = (matrix_x[2] - matrix_x[1]) / 6.0 85 86 s = a + b * x + c * x * x + d * x * x * x 87 return s 88 89 def SplineInterpolationNotAKnot4(self, x, y1, y2, y3, y4): 90 # 无法使用TDMA计算 91 matrix_x = self.Simplified_Not_A_Knot4(y1, y2, y3, y4) 92 93 a = y2 94 b = y3 - y2 - matrix_x[1] / 3.0 - matrix_x[2] / 6.0 95 c = matrix_x[1] / 2.0 96 d = (matrix_x[2] - matrix_x[1]) / 6.0 97 98 s = a + b * x + c * x * x + d * x * x * x 99 return s 100 101 def biSpline4(self, srcImg, dstH, dstW): 102 dstH, dstW = int(dstH), int(dstW) 103 srcH, srcW, _ = srcImg.shape 104 srcImg = np.pad(srcImg, ((1, 2), (1, 2), (0, 0)), 'edge') 105 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8) 106 for dstY in range(dstH): 107 for dstX in range(dstW): 108 for channel in [0, 1, 2]: 109 # p11 p12 p13 p14 110 # 111 # p21 p22 p23 p24 112 # p 113 # p31 p32 p33 p34 114 # 115 # p41 p42 p43 p44 116 # 储存为 p(y, x) 117 p = [dstY * srcH / dstH, dstX * srcW / dstW] 118 p22 = [math.floor(p[0]), math.floor(p[1])] 119 p21 = [p22[0], p22[1] - 1] 120 p23 = [p22[0], p22[1] + 1] 121 p24 = [p22[0], p22[1] + 2] 122 123 p11 = [p21[0] - 1, p21[1]] 124 p12 = [p11[0], p22[1]] 125 p13 = [p11[0], p23[1]] 126 p14 = [p11[0], p24[1]] 127 128 p31 = [p21[0] + 1, p21[1]] 129 p32 = [p31[0], p22[1]] 130 p33 = [p31[0], p23[1]] 131 p34 = [p31[0], p24[1]] 132 133 p41 = [p21[0] + 2, p21[1]] 134 p42 = [p41[0], p22[1]] 135 p43 = [p41[0], p23[1]] 136 p44 = [p41[0], p24[1]] 137 138 diff_y, diff_x = p[0] - p22[0], p[1] - p22[1] 139 r1 = self.SplineInterpolationNatural4(diff_x, srcImg[p11[0], p11[1], channel], srcImg[p12[0], p12[1], channel], srcImg[p13[0], p13[1], channel], srcImg[p14[0], p14[1], channel]) 140 r2 = self.SplineInterpolationNatural4(diff_x, srcImg[p21[0], p21[1], channel], srcImg[p22[0], p22[1], channel], srcImg[p23[0], p23[1], channel], srcImg[p24[0], p24[1], channel]) 141 r3 = self.SplineInterpolationNatural4(diff_x, srcImg[p31[0], p31[1], channel], srcImg[p32[0], p32[1], channel], srcImg[p33[0], p33[1], channel], srcImg[p34[0], p34[1], channel]) 142 r4 = self.SplineInterpolationNatural4(diff_x, srcImg[p41[0], p41[1], channel], srcImg[p42[0], p42[1], channel], srcImg[p43[0], p43[1], channel], srcImg[p44[0], p44[1], channel]) 143 144 c = self.SplineInterpolationNatural4(diff_y, r1, r2, r3, r4) 145 146 dstImg[dstY, dstX, channel] = np.clip(c, 0, 255) 147 return dstImg
Lanzos插值
同样的是卷积的思路,只是卷积核变成了下式
L(x)=\begin{cases}
sinc(x)sinc(x/a), &-a<x<a \\
0, &otherwise
\end{cases}
将三次卷积插值的代码稍作修改即可
1 class BiLanczosInterpolation: 2 @staticmethod 3 def LanczosConvKernel(s, a): 4 if s == 0: 5 return 1 6 elif abs(s) <= a: 7 return a * np.sin(np.pi * s) * np.sin(np.pi * s / a) / (pow(np.pi, 2) * pow(s, 2)) 8 else: 9 return 0 10 11 def biLanczos4(self, srcImg, dstH, dstW): 12 # p11 p12 p13 p14 13 # 14 # p21 p22 p23 p24 15 # p 16 # p31 p32 p33 p34 17 # 18 # p41 p42 p43 p44 19 dstH, dstW = int(dstH), int(dstW) 20 scrH, scrW, _ = srcImg.shape 21 srcImg = np.pad(srcImg, ((1, 1), (1, 1), (0, 0)), 'edge') 22 dstImg = np.zeros((dstH, dstW, 1), dtype=np.uint8) 23 convKernelIndex = [-1, 0, 1, 2] 24 for dstY in range(dstH): 25 for dstX in range(dstW): 26 for channel in [0]: 27 y = dstY * scrH / dstH 28 x = dstX * scrW / dstW 29 y1 = math.floor(y) 30 x1 = math.floor(x) 31 32 array = [] 33 for i in convKernelIndex: 34 temp = 0 35 for j in convKernelIndex: 36 temp += srcImg[y1 + i, x1 + j, channel] * self.LanczosConvKernel(x - (x1 + j), 2) 37 array.append(temp) 38 39 temp = 0 40 for i in convKernelIndex: 41 temp += array[i + 1] * self.LanczosConvKernel(y - (y1 + i), 2) 42 dstImg[dstY, dstX, channel] = np.clip(temp, 0, 255) 43 44 return dstImg 45 46 def biLanczos6(self, srcImg, dstH, dstW): 47 # p11 p12 p13 p14 p15 p16 48 # 49 # p21 p22 p23 p24 p25 p26 50 # 51 # p31 p32 p33 p34 p35 p36 52 # p 53 # p41 p42 p43 p44 p45 p46 54 # 55 # p51 p52 p53 p54 p55 p56 56 # 57 # p61 p62 p63 p64 p65 p66 58 dstH, dstW = int(dstH), int(dstW) 59 scrH, scrW, _ = srcImg.shape 60 srcImg = np.pad(srcImg, ((2, 2), (2, 2), (0, 0)), 'edge') 61 dstImg = np.zeros((dstH, dstW, 1), dtype=np.uint8) 62 convKernelIndex = [-2, -1, 0, 1, 2, 3] 63 for dstY in range(dstH): 64 for dstX in range(dstW): 65 for channel in [0]: 66 y = dstY * scrH / dstH 67 x = dstX * scrW / dstW 68 y1 = math.floor(y) 69 x1 = math.floor(x) 70 71 array = [] 72 for i in convKernelIndex: 73 temp = 0 74 for j in convKernelIndex: 75 temp += srcImg[y1 + i, x1 + j, channel] * self.LanczosConvKernel(x - (x1 + j), 3) 76 array.append(temp) 77 78 temp = 0 79 for i in convKernelIndex: 80 temp += array[i + 1] * self.LanczosConvKernel(y - (y1 + i), 3) 81 dstImg[dstY, dstX, channel] = np.clip(temp, 0, 255) 82 83 return dstImg 84 85 def biLanczos8(self, srcImg, dstH, dstW): 86 # p11 p12 p13 p14 p15 p16 p17 p18 87 # 88 # p21 p22 p23 p24 p25 p26 p27 p28 89 # 90 # p31 p32 p33 p34 p35 p36 p37 p38 91 # 92 # p41 p42 p43 p44 p45 p46 p47 p48 93 # p 94 # p51 p52 p53 p54 p55 p56 p57 p58 95 # 96 # p61 p62 p63 p64 p65 p66 p67 p68 97 # 98 # p71 p72 p73 p74 p75 p76 p77 p78 99 # 100 # p81 p82 p83 p84 p85 p86 p87 p88 101 dstH, dstW = int(dstH), int(dstW) 102 scrH, scrW, _ = srcImg.shape 103 srcImg = np.pad(srcImg, ((3, 3), (3, 3), (0, 0)), 'edge') 104 dstImg = np.zeros((dstH, dstW, 1), dtype=np.uint8) 105 convKernelIndex = [-3, -2, -1, 0, 1, 2, 3, 4] 106 for dstY in range(dstH): 107 for dstX in range(dstW): 108 for channel in [0]: 109 y = dstY * scrH / dstH 110 x = dstX * scrW / dstW 111 y1 = math.floor(y) 112 x1 = math.floor(x) 113 114 array = [] 115 for i in convKernelIndex: 116 temp = 0 117 for j in convKernelIndex: 118 temp += srcImg[y1 + i, x1 + j, channel] * self.LanczosConvKernel(x - (x1 + j), 4) 119 array.append(temp) 120 121 temp = 0 122 for i in convKernelIndex: 123 temp += array[i + 1] * self.LanczosConvKernel(y - (y1 + i), 4) 124 dstImg[dstY, dstX, channel] = np.clip(temp, 0, 255) 125 126 return dstImg
感谢
如何直观地理解拉格朗日插值法? https://www.zhihu.com/question/58333118 图像处理中的三次卷积插值(Cubic Convolution) https://blog.csdn.net/shiyimin1/article/details/80141333 Bicubic interpolation https://en.wikipedia.org/wiki/Bicubic_interpolation Cubic convolution interpolation for digital image processing (1981) https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.320.776 三次样条插值(Cubic Spline Interpolation)及代码实现(C语言) https://www.cnblogs.com/xpvincent/archive/2013/01/26/2878092.html Spline interpolation https://en.wikipedia.org/wiki/Spline_interpolation Lanczos resampling https://en.wikipedia.org/wiki/Lanczos_resampling


 浙公网安备 33010602011771号
浙公网安备 33010602011771号