力扣leetcode45. 跳跃游戏 II
做的时候非常困惑，为什么贪心能用，看了题解也没有解决困惑，于是自己思考了一下
代码就用官方题解的了，先贴个代码，看懂很容易，但是从评论来看，很容易产生困惑，为什么这个题可以用贪心，如果题目改成，只能跳到目标长度，那么还能贪心吗，答，不能
1 class Solution(object): 2 def jump(self, nums): 3 step, end, max_bound = 0, 0, 0 4 for i in range(len(nums) - 1): 5 max_bound = max(max_bound, i + nums[i]) 6 if i == end: 7 step += 1 8 end = max_bound 9 return step
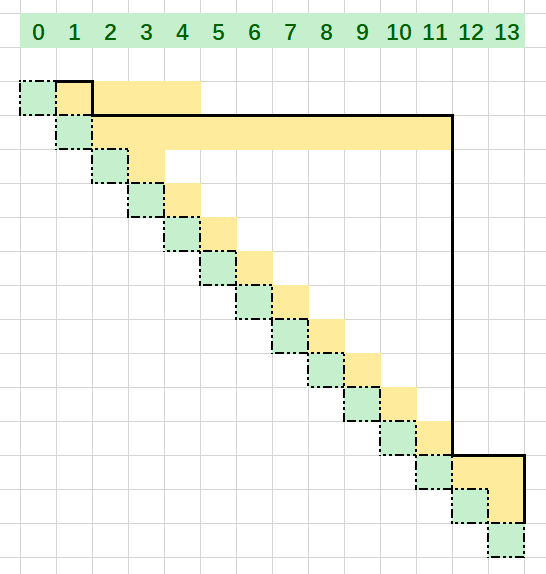
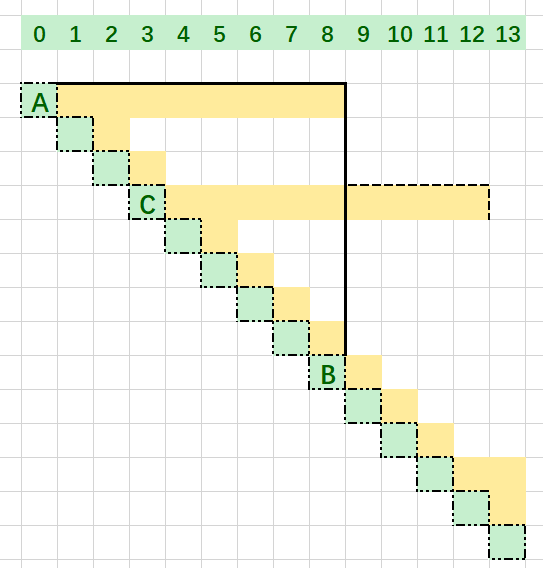
这个题目如果用图画出来就是这样的，只能用横线和竖线从左上角向右下角延伸，找到使得竖线条数最少的解，因为不存在两条连续的横线或两条连续的竖线（即为一条线）以及横竖交替会改变方向，那么，横竖的数量一定相等（如图的黑线当然不成立，因为横线必须紧附黄块）
那么我们让黑线紧附黄块上沿，得到下图
这时候横线和竖线的数量都是3，也就是答案（做题时画简易图的时候甚至开始想凸包算法了，方向错了.jpg）
不过这个图有一个问题，在于，拐点不在绿色的方块上，但对于此题，这个就不是问题了，因为横线和竖线在平移和改变长度时不改变数量，因此上图就转换成下图，也就是这个例子的正解
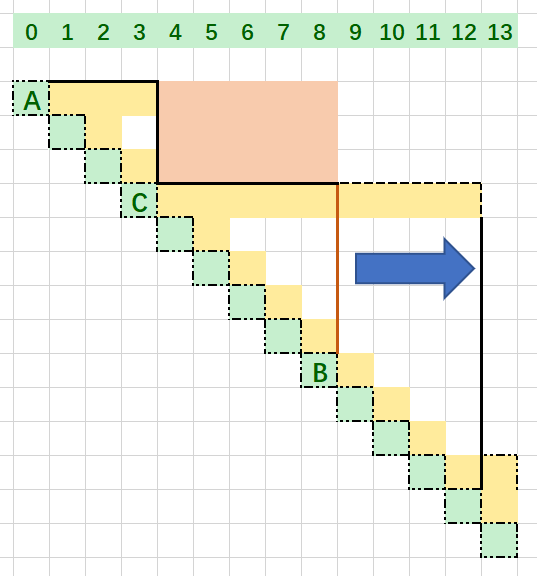
为什么可以这么平移，因为这背后的隐藏线是这样的
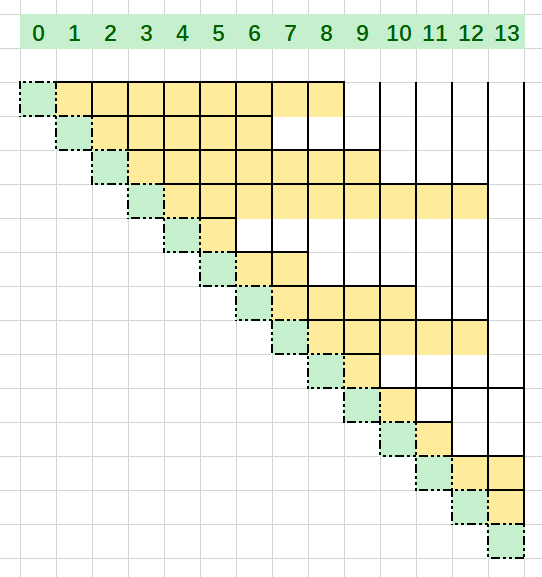
所有竖线都是贯通的，横线和黄块长度相同，也就是，假设 i 方块最远可以到达 i + n 方块，那么，他一定可以到达
[i, i + n] 之间所有的方块，那么，平移的问题就解决了
不过如果数据都如下所示，那么这题问题都解决了
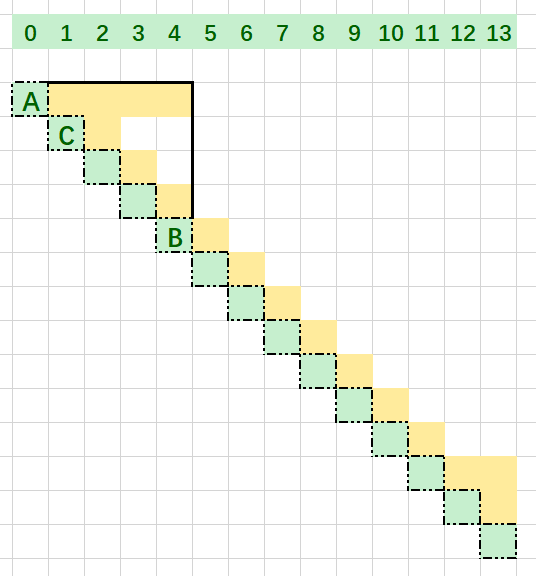
而很多情况会如下所示，这就让人思考，会不会产生局部最优解
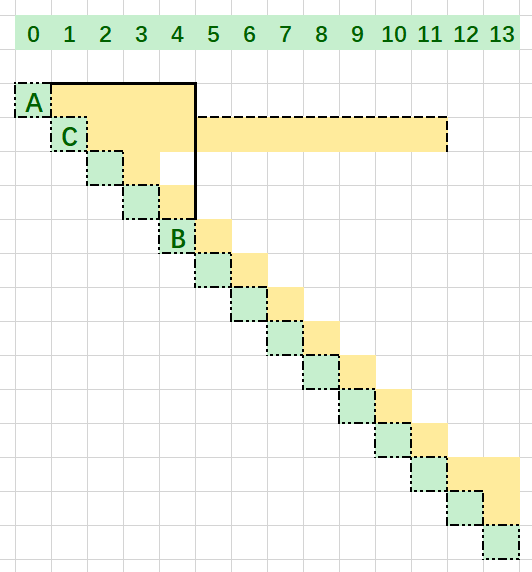
如果理解了平移的问题，那么，所有的局部最优解都可以发生转化，即A->B中产生了更长的C，那么A一定可以到达C，然后达到最远的距离，同时黑线与方块接触时计数一次
再来个栗子
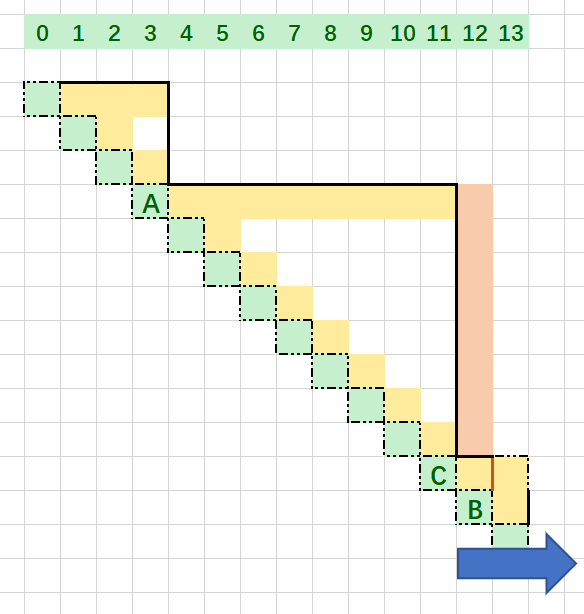
完全相同的操作，而剩下的不会超过A->B长度的，自然就不用考虑了
那么解决最后一个困惑，0怎么办，题目中说明了一点，一定存在解，那么，0一定不是关键点A，他在作为C时，长度肯定小于A->B，那么就不会产生任何的干扰了
如有错误，望指正
