2.区间扫描线算法——>被认为是消隐算法中最快的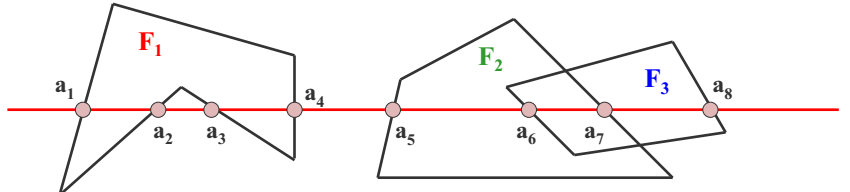
扫描线的交点把这条扫描线分成了若干个区间,每个区间上必然是同一种颜色。对于有重合的区间,如a6a7这个区间,要么显示F2的颜色要么显示F3的颜色,不会出现颜色的跳跃。
要实现这个算法:
1>首先要有投影多边形;
2>然后求交点;
3>交点进行排序;
4>在每个区间找当中的一个象素(i,j),在(i,j)处计算每个相关面的z值,对相关深度值z进行比较,其中最大的一个就表示是可见的,整个这段区间就画这个z值最大面的颜色。
【确定小区间的颜色】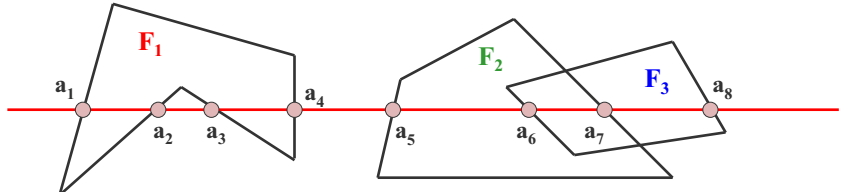
(1)小区间上没有任何多边形,就用背景色显示,如[a4,a5];
(2)小区间只有一个多边形,就显示该多边形的颜色,如[a1,a2];
(3)小区间上存在两个或两个以上的多边,就必须通过深度测试判断那个多边形可见,如[a6,a7]。
3.区域子分割算法(Warnock算法)
【采用了分而治之的思想,利用了堆栈的数据结构】
把物体投影到全屏幕窗口上,然后递归分割窗口,直到窗口内目标【足够简单】,可以显示为止。
3.1【足够简单是指】
(1)窗口内仅包含一个多边形;
(2)窗口与一个多边形相交,且窗口内无其他多边形;
(3)窗口被一个多边形所包围;
(4)窗口与一个多边形相离。
——>【窗口与多边形的关系:包含/相交/包围/相离】
【判断多边形与窗口是分离的】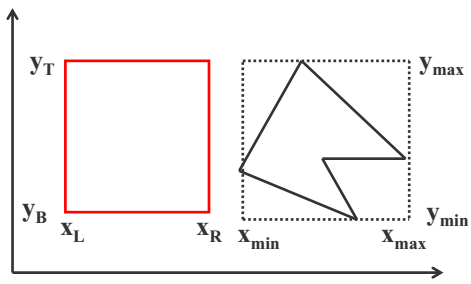
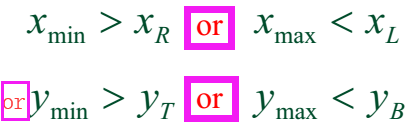
【判断多边形在窗口内】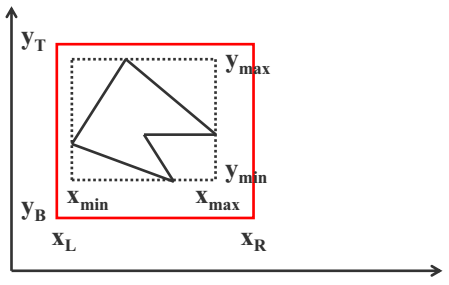
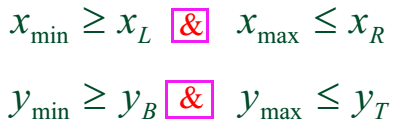
【判断多边形与窗口相交,可以采用直线方程作为判别函数来判断】
3.2窗口有多个多边形投影面,如何显示?【分而治之】
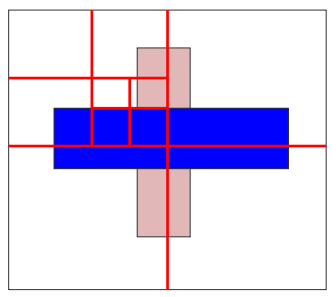
(1)若窗口内没有物体则按照背景色显示;
(2)若窗口内只有一个面,则把该面显示出来;
(3)若窗口内含有两个以上的面,则把窗口等分成四个子窗口,对每个小窗口再做上述同样的处理。
(4)若到某个时刻,【窗口仅有象素那么大】,而窗口内仍有两个以上的面,这时不必再分割,只要取窗口内【最近的】可见面的颜色或所有可见面的【平均颜色】作为该象素的值。
【假设显示器分辨率1024*1024,窗口最多分几次?10次】
二、光栅扫描算法小结
1、直线段的扫描转换算法
(1)DDA算法利用了直线的【斜截式方程】(y=kx+b),引进了【增量思想】(把一个乘法和一个加法变成一个加法);
(2)中点法采用直线的【一般式方程】,引进了【增量思想】,比DDA算法的优点是采用了【整数加法】;
(3)Bresenham算法采用了【增量和整数算法】,还可以用于二次曲线。
2、多边形的扫描转换和区域填充
有四个步骤:求交、排序、配对、填色。引进了【图形的连贯性】,手段就是利用了【增量算法】和【特殊的数据结构】。
3、直线和多边形裁剪
cohen-Sutherland算法的核心思想是【编码】,把屏幕分成【9个区域】,用【4位编码】描述这9个区域,通过4位编码的“与”、“或”运算来判断直线段是在窗口内或外。
Liang-Barsky算法用【参数方程】表示,把被裁剪的直线段看成是一条【有方向的线段】,把窗口的四条边分成两类(入边和出边)
4、走样和反走样
反走样主要有三种方法:提高分辨率、区域采样、加权区域采样。
5、消隐
z-buffer算法把数组变成了【单个变量】;
区间扫描线算法把逐点处理变成【逐段处理】,提高算法效率;
Warnock算法采用了【分而治之】的思想,利用【堆栈】的数据结构。
核心思想:
(1)增量思想
(2)编码思想
(3)符号判断—>整数算法
(4)图形的连贯性
(5)分而治之



 浙公网安备 33010602011771号
浙公网安备 33010602011771号