扫描转换算法重要的意义是提出了图形学里两个重要的思想:
(1)扫描线;
(2)增量思想。
已经知道X-扫描线算法效率低是因为求交麻烦,那求教点的时候能否也采用增量思想,每条扫描线的y值都知道,关键是求x值。
可以从三个方面改进:
1、在处理一条扫描西线时,仅对与它相交的多边形的边(有效边)进行求交运算。
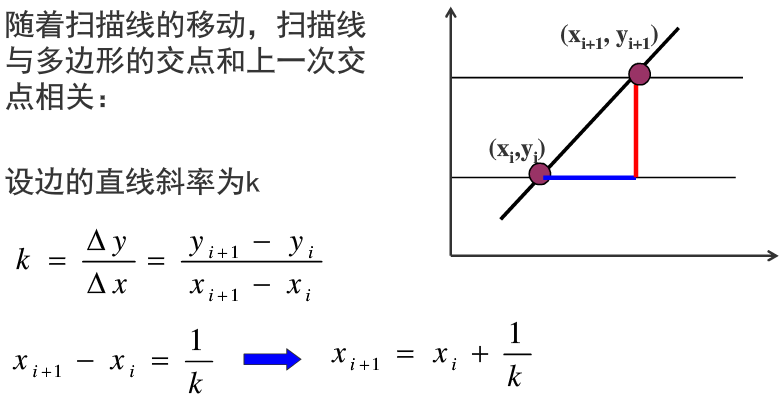
2、考虑扫描线的连贯性,也就是当前扫描线与各边交点顺序与下一条扫描线边与各边的交点顺序很可能相同或非常相似。
3、考虑多边形的连贯性,即当某条边与扫描线相交时它很可能与下一条扫描线也相交。
(2)改进的X-扫描线算法:【无法实现对未知边界的区域填充】
【增量思想/连贯性思想/构建一套特殊的数据结构】
为了避免求交运算——>需要特殊的数据结构:
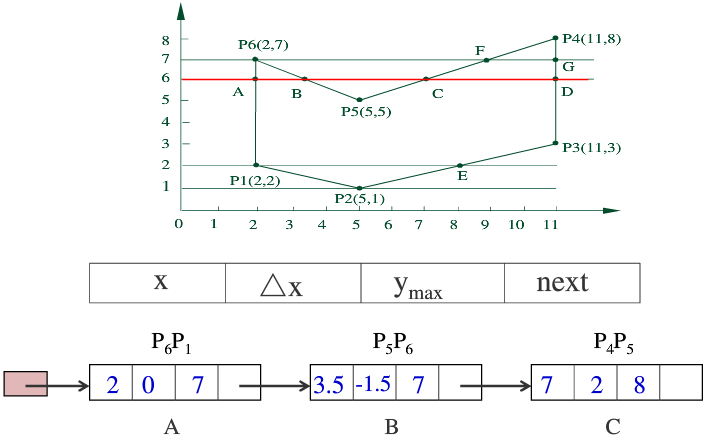
a)活性边表(AET):把当前扫描线相交的边称为活性边,并把它们按与扫描线交点x坐标递增的顺序存放在一个链表中。
b)节点内容:x:当前扫描线与边的交点坐标
x2-x1:从当前扫描线到下一条扫描线间x的增量——>x2-x1=1/k
ymax:该边所交的最高扫描线的坐标值
next:指向下一条边的指针
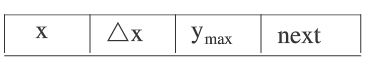
C)新边表(NET):为了方便活性边表的建立与更新,用来存放多边形的边的信息。
1.构造一个纵向链表,长度为多边形所占有的最大扫描线数,链表的每个结点称为吊桶;
2.新边表(NET)挂在与【该边低端y值相同】的扫描线桶中;
ymax:该边的最大值;
xmin:该边较低点的x坐标值xmin;
1/k:该边的斜率
ymax:指向下一条具有相同较低端y坐标的边的指针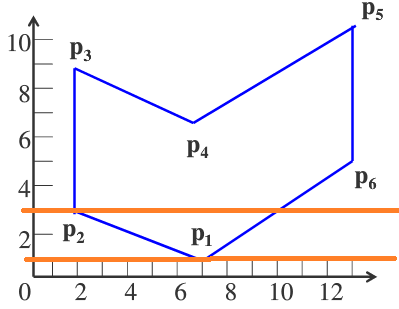
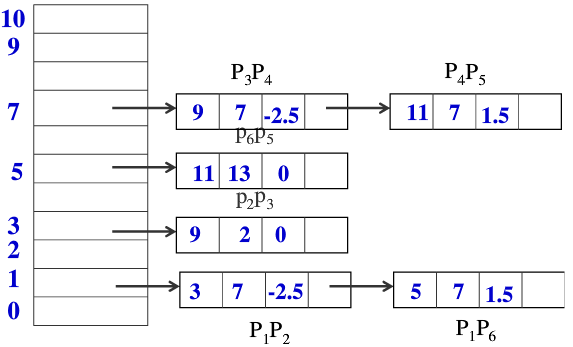
d)每做一次新的扫描时,要对已有的边进行三个处理:
1.是否被去除掉;
2.若不被去除掉,就要对它的数据进行更新,x=x+1/k;
3.是否有新的边进来,新的边在NET里,可以插入排序插进来。
多边形扫描转换算法:
【小结】
为提高算法效率:
(1)增量的思想;
(2)连贯性思想;
(3)构建一套特殊的数据结构。
【缺点】这里的区间端点通过计算扫描线与多边形边界的交点获得,所以待填充区域的边界线必须预先知道,因此它的缺点所在是无法实现对未知边界的区域填充。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号