二、多边形的扫描转换
在光栅图形中,区域是由【相连的】像素组成的集合,这些像素具有【相同的】属性值或者它们位于某边界线的内部
1、多边形的扫描转换—>光栅图形的一个基本问题是把多边形的顶点表示转换为点阵表示。【缺点:无法实现对未知边界的区域填充】
2、多边形的扫描转换与区域填充问题—>是怎样在离散的像素集上表示一个连续的二维图形。
3、多边形有两种重要的表示方法: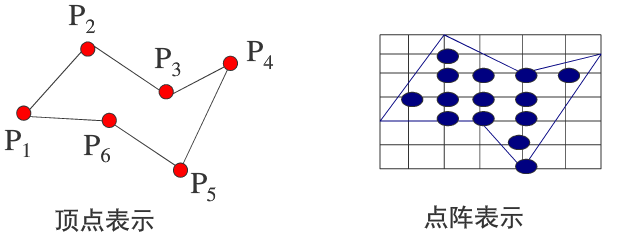
(1)顶点表示:用多边形的定点序列来表示多边形
优点:直观、几何意义强、占内存少、易于进行几何变换
缺点:没有明确指出那些象素在多边形内,故不能直接用于上色
(2)点阵表示:是用位于多边形内的象素集合来刻画多边形
缺点:丢失了许多几何信息(eg:边界、顶点等)
——>但【点阵表示是光栅显示系统显示时所需的表现形式。】
4、多边形分类
5、【问题1】知道多边形的边界,如何找到多边形内部的点,即把多边形内部填上颜色?
(1)X-扫描线算法;
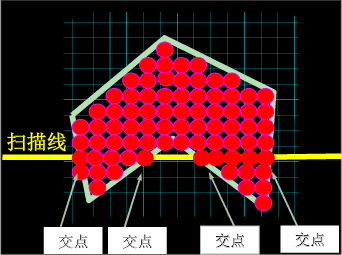
按扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的象素,即完成填充工作。区间的端点可以通过计算扫描线与多边形边界线的交点获得。
【核心:按x递增顺序排列交点的x坐标序列,缺点:效率低(求交点很麻烦)】
算法步骤:
1.确定多边形所占有的最大扫描线数,得到多边形定点的最小最大值;
2.从ymin到ymax每次用一条扫描线进行填充;
3.对一条扫描线填充的过程分为四个步骤:
a)求交点;
b)把所有交点按递增顺序排序;
c)交点配对(第一个和第二个,第三个和第四个);
d)区间填色。
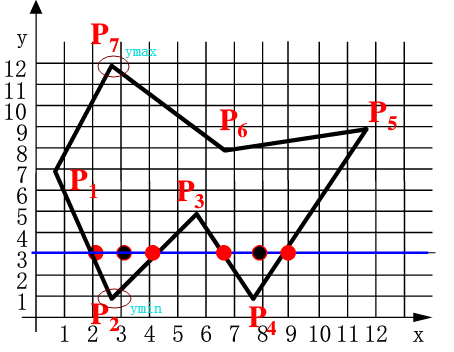
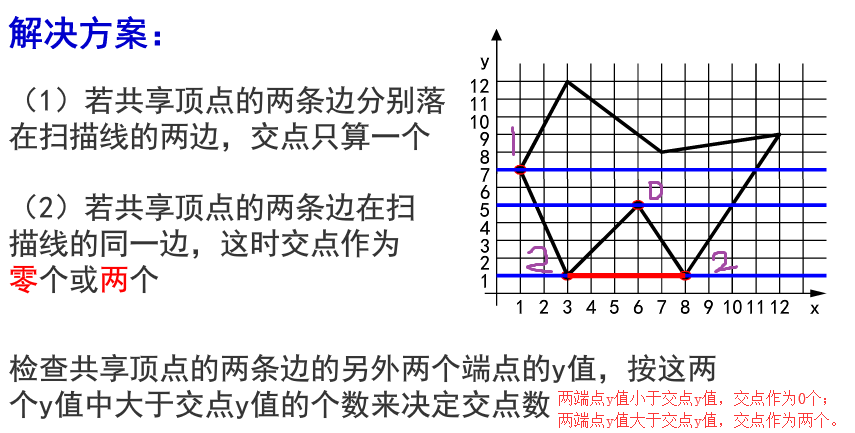
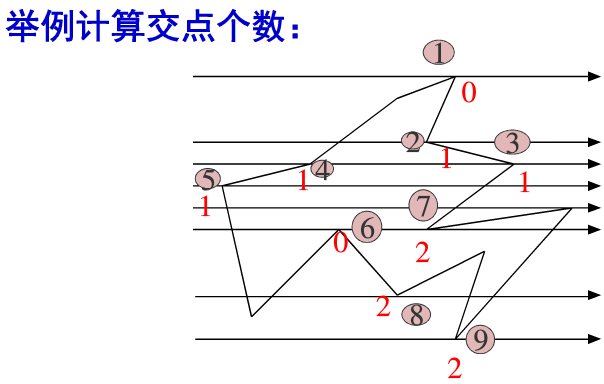
扫描线与多边形顶点相交时,交点的取舍问题【交点应保证为偶数个】: