一、直线段的扫描转换算法
为了在光栅显示器上用这些离散的象素点逼近这条直线,需要知道这些象素点的x,y坐标,【沿x方向前进一个象素(步长=1)】,可以算出相应的y值。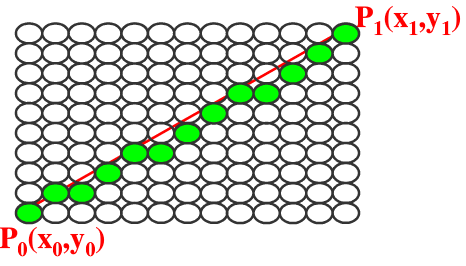
1、求出过P0,P1的直线段方程: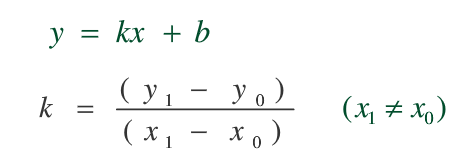
因为象素坐标是整数,所以【y值还要取整处理——>四舍五入】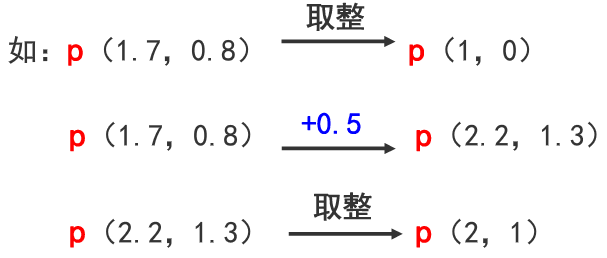
P取整为P(1,0)时偏差太大,做+0.5的处理后更加逼近
一个动画或真实感图像往往需要调用成千上万次画线程序,因此直线算法的好坏与效率将直接影响图像的质量和显示速度。
【为了提高效率——>去乘法】
2、直线绘制的三个著名的常用算法
(1)数值微分法(DDA) ——>【引入了增量思想,采用了直线斜截式方程】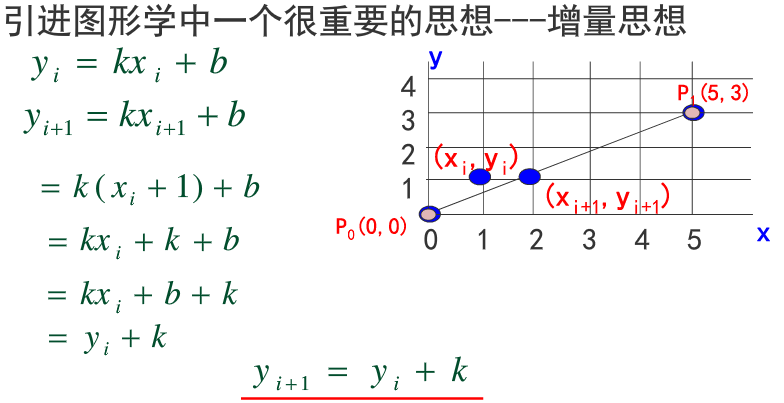
式子的含义是:当前步的y值等于前一步的y值加上斜率k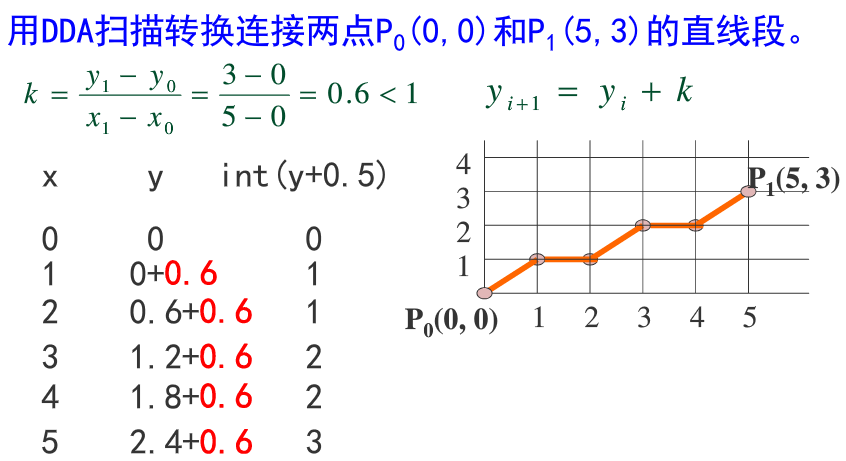
【思考】1、DDA画直线算法:x每递增1,y递增斜率k。是否适合任意斜率的直线?
————> |K| <= 1 <————
————> |K| > 1 光栅太稀疏了! <————
2、DDA画直线算法是否最优?若非,如何改进?
——>
a.改进效率:
一般情况下k与y都是小数,每一步都要对y四舍五入后取整——>唯一途径:把浮点运算变成整数加法
b.从直线方程类型做文章:
如两点式、一般式



