高斯金字塔的形成过程：
对某一灰度图像，首先进行升采样（即扩大两倍采样），然后对升采样之后的图片进行高斯模糊，从而生成一组采样图。（注：升采样不是必须的）
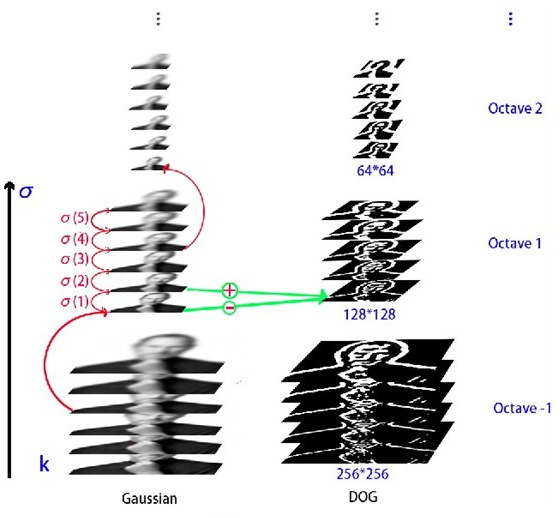
对原灰度图像进行降采样，然后高斯模糊，得到第二组采样图，每一组都有六层尺寸相同但模糊系数不同的采样图像得到。为了保持差分高斯金字塔的尺度空间（即模糊系数）的连续性，下一组（第i组）的第一层由上一组的第四层降采样之后得到，同时第i组的后面几层都是由该组第一层经过高斯模糊得到，不需要进行降采样。这样，几组采样图组合在一起，就构成了高斯金字塔。如下图所示：
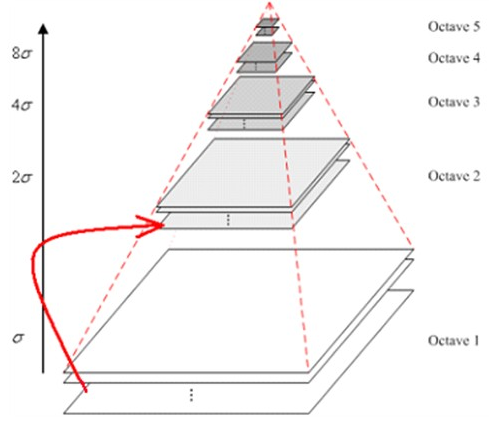
组数是由原始图片的行数和列数决定的：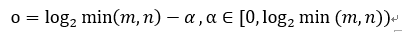
，o表示高斯金字塔的组数，m和n分别表示图像的行和列。α为塔顶图像的最小维数的对数值。例如，对于大小为512*512的图像来说，金字塔上各层图像的大小如下表所示。当塔顶图像为4*4时，α=2，o=7;当塔顶图像大小为2*2时，α=1，o=8。
| 塔顶图像大小 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 金字塔层数o | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
差分高斯金字塔的建立（结论性知识）：
2002年Mikolajczyk在详细的实验比较中发现尺度归一化的高斯拉普拉斯函数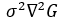
的极大值和极小值同其他的特征提取函数（例如：梯度，Hessian或者Harris角特征）比较，能够产生最稳定的图像特征。
Lindeberg在1994年发现高斯差分函数（Difference of Gaussian，简称DOG算子）与尺度归一化的高斯拉普拉斯函数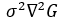非常近似。
其中，D（x,y,σ）和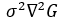的关系可以从如下推导中得出：
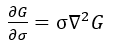
利用差分近似代替微分，则有：
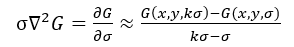
因此有：
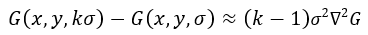，其中k-1为常数，并不影响极值点的求取。
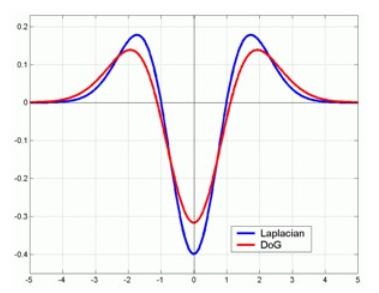
高斯拉普拉斯与高斯差分的比较如下图：
Lowe使用更高效的高斯差分算子代替拉普拉斯算子进行极值检测，如下：
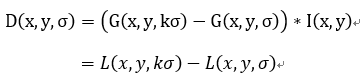
其中，图像的尺度空间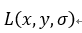
定义为变化尺度的高斯函数
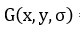与原图像
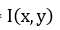的卷积：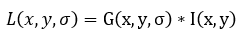
在实际计算中，每一组采样图中的每两层图像之间相减（下一层减上一层），就构成了差分高斯金字塔。
下图为构建DOG金字塔的示意图，原图采用128*128的图像，扩大一倍后构建金字塔。
尺度空间：
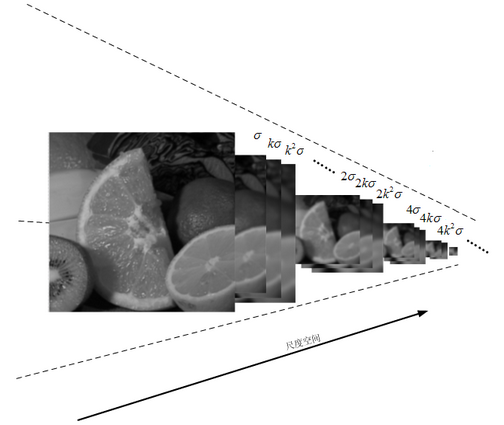
在高斯金字塔中，有两个参数很重要，一个是第几组o，一个是某一组中的第几层s，这两个量合起来（o，s）就构成了高斯金字塔的尺度空间。变量o控制的是金字塔中尺寸这个尺度，s用来区分同一个尺寸尺度下的图像，s确定了一个组中不同的模糊成度。这样，（o，s）就可以确定高斯金字塔中的唯一一副图像。
根据lowe论文中指出，（o，s）作用于一幅图像是通过下列公式实现的：
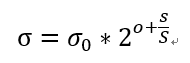，其中，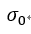
为高斯模糊初始值，Lowe建议取为1.6。S为每组的层数，即S=3。
下图形象的说明了什么是尺度空间：
尺度空间的连续性：
为什么高斯金字塔的每层有S+3幅图像？
假设我们在每一组图像中求S层点，那么为了获得S层点，在差分高斯金字塔中需要有S+2层图像，那么在高斯金字塔中就必须有S+3层图像了（差分高斯金字塔由高斯金字塔相减得到）。
那么，为什么要假设求S层点呢，答案是为了保持尺度的连续性！下面详细分析：
令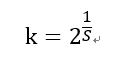
，Lowe取S=3，所以K=2^1/3。
假设当前所在组为第0组，则当前组中各高斯图像的尺度依次为：
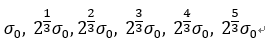
当前组中各差分高斯图像的尺度依次为：
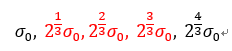（因为每个相邻的高斯图像相减之后，得到的仍然是轮廓更加清晰地图片，分辨率也是前一层高斯模糊之后的分辨率，也就是比较高的那个）
我们可以推测出，下一组高斯图像的尺度依次为：
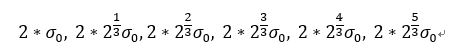（因为下一组的第一层是上一组的第四层下采样之后得到的）
下一组中各差分高斯图像的尺度依次为：
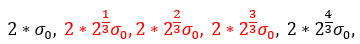
其中红色标注数据所代表的层，是差分高斯金字塔中获得极值点的层，也就是说只有在这些层上才发生与上下两层比较获得极值点的操作。
下面将这些红色数据连成串：2^(1/3)σ， 2^(2/3)σ， 2^(3/3)σ，2×2^(1/3)σ，2×2^(2/3)σ，2×2^(3/3)σ......这些数据是连续的！
我们通过在每个八度中多构造三幅高斯图像，达到了尺度空间连续的效果，这一效果带来的直接的好处是在尺度空间的极值点确定过程中，我们不会漏掉任何一个尺度上的极值点，而是能够综合考虑量化的尺度因子
所确定的每一个尺度！
