计算机组成原理- 第二章 数据的表示和运算
第二章 数据的表示和运算
考纲内容
- 数制与编码
- 进位计数制及其相互转化
- 真值和机器数
- 字符和字符串
- 定点数的表示和运算
- 表示: 无符号数: 有符号数
- 运算:定点数移位运算;原码定点数加减运算;补码定点数加减运算;定点数乘除运算,溢出的概念及其判别方法
- 浮点数的表示和运算
- 浮点数的表示:IEEE754标准
- 运算: 浮点数的加减运算
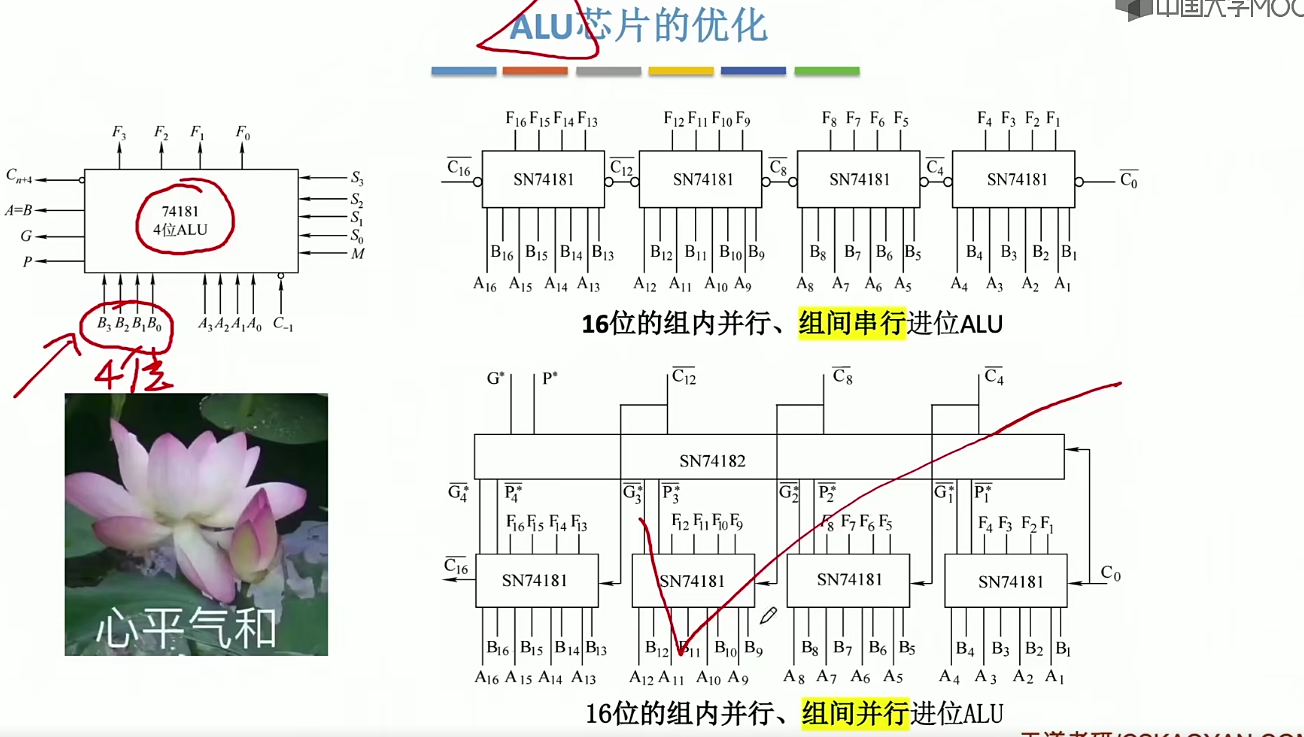
- 算术逻辑单元(ALU)
- 串行加法器和并行加法器;ALU的功能和构造
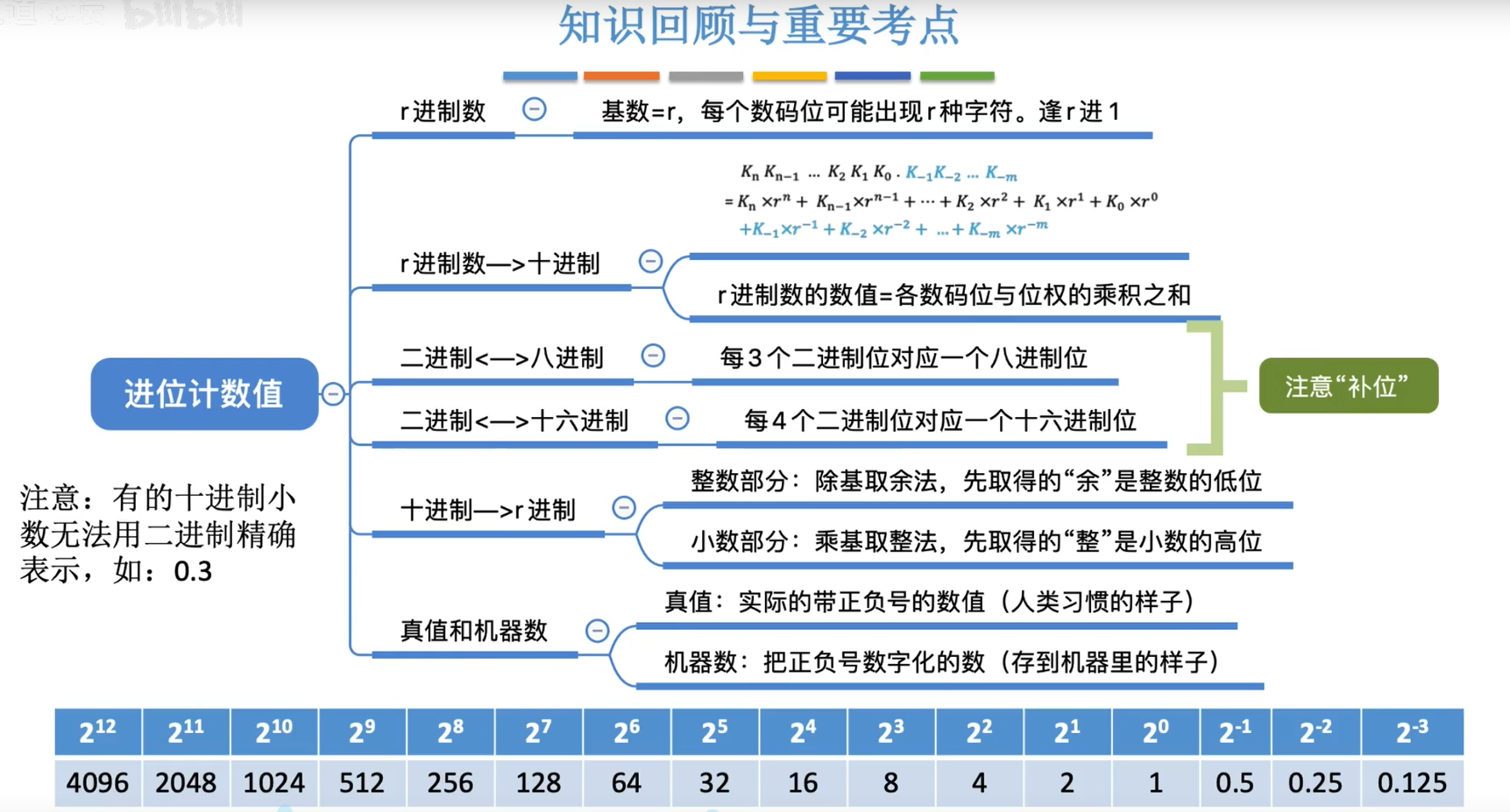
1.1进位计数制
1.1.1其他进制转换十进制
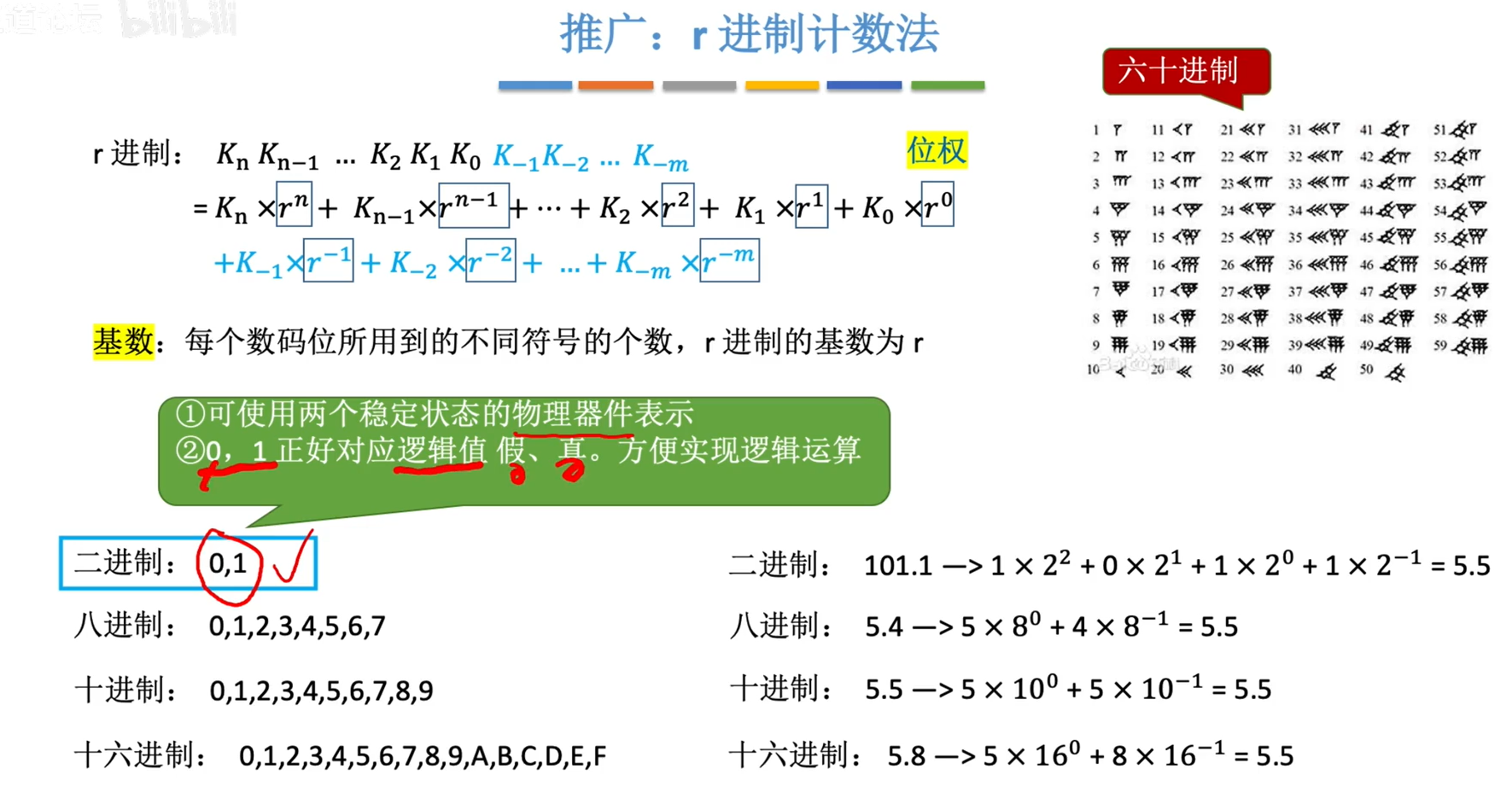
1.1.2二进制,八进制,十六进制相互转换

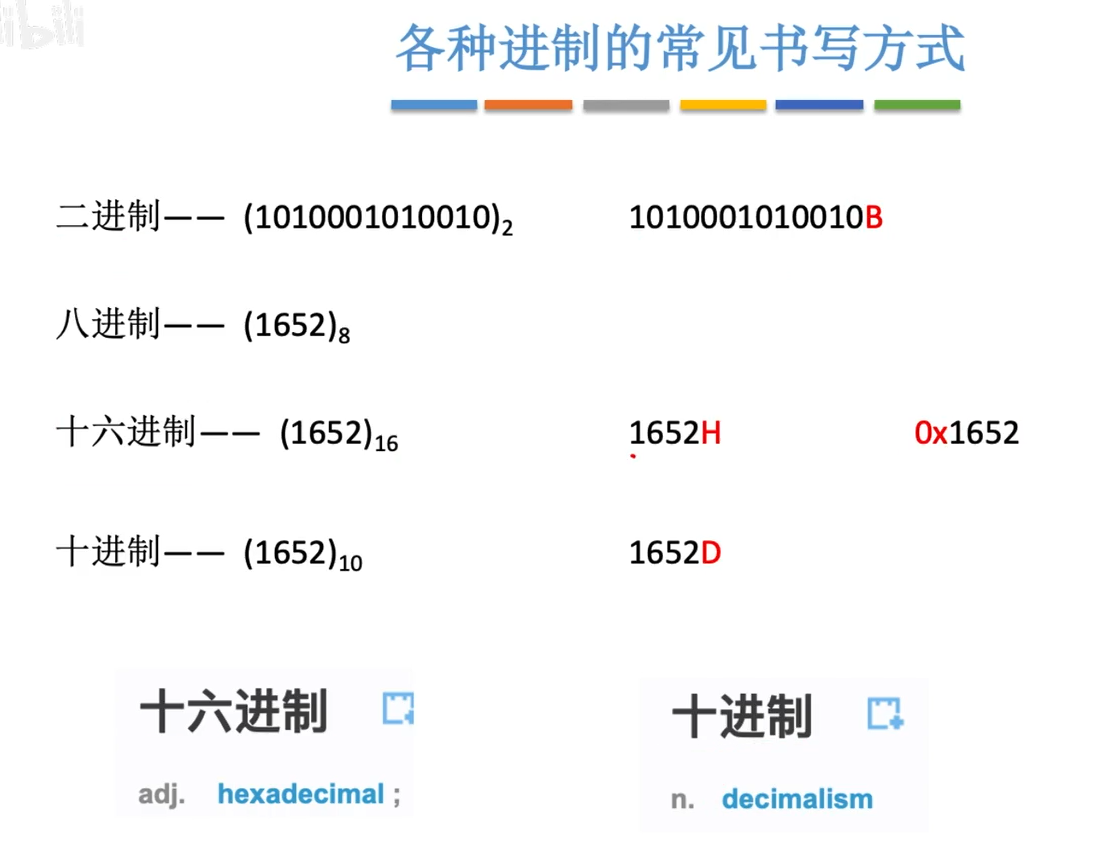
1.1.3十进制转换成其他进制


1.1.4真值和机器数

1.1.5小结
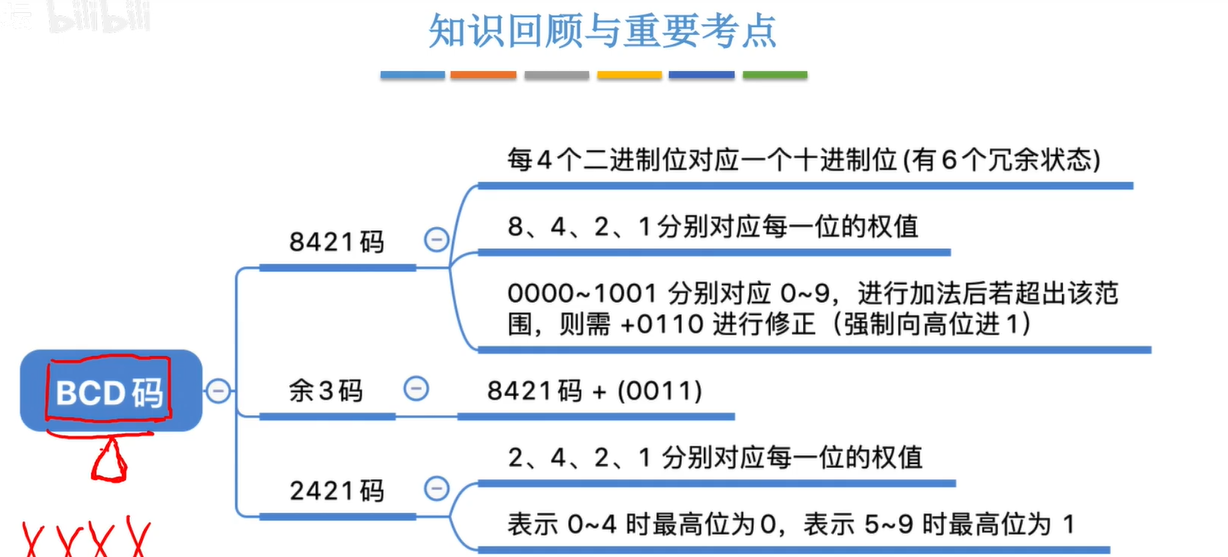
1.2 BCD码
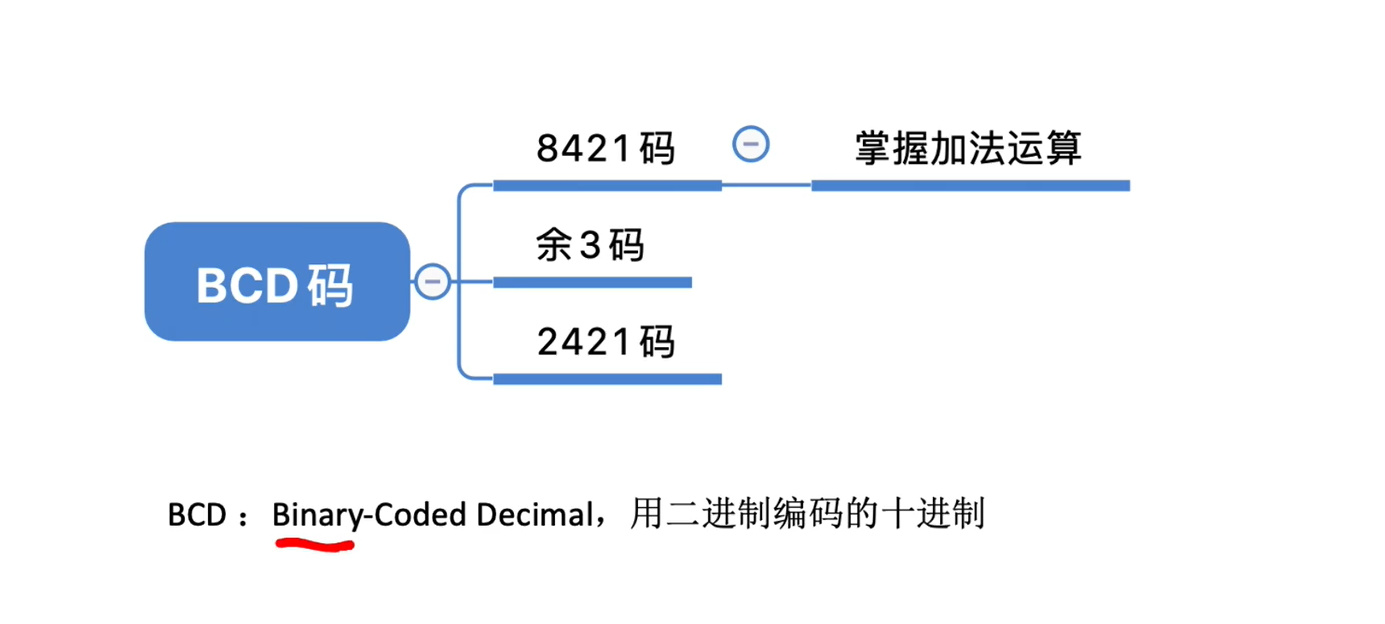
1.2.1 8424码
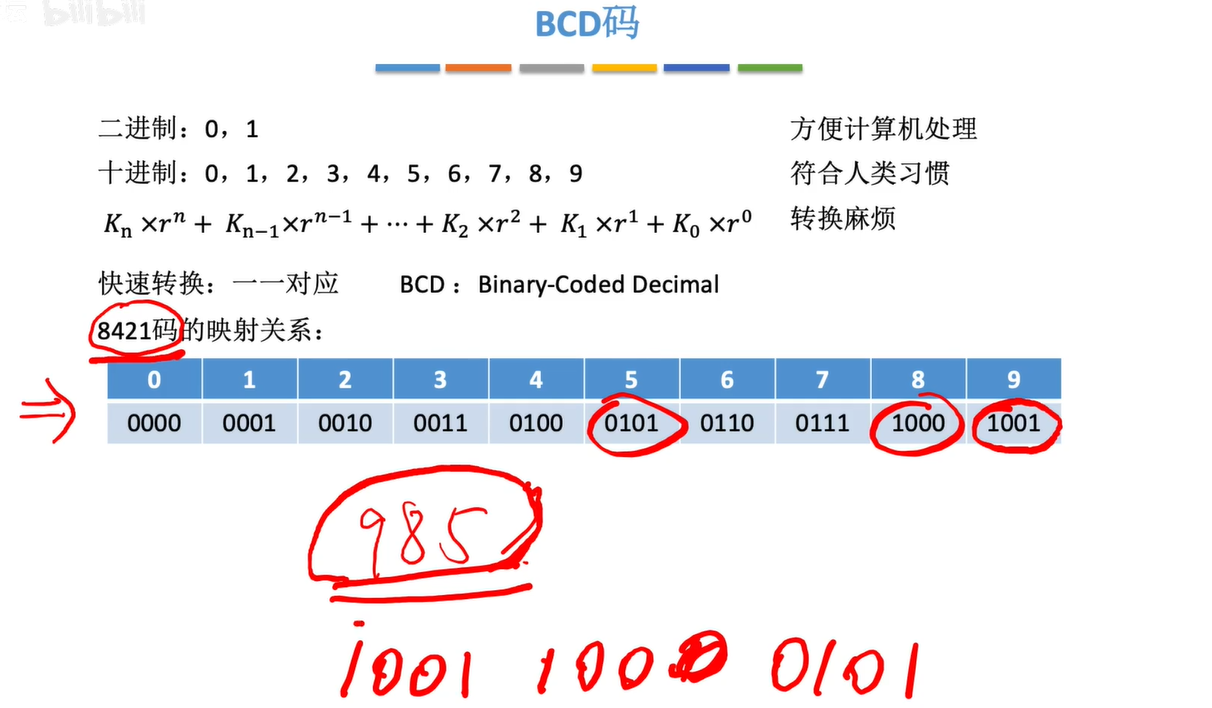
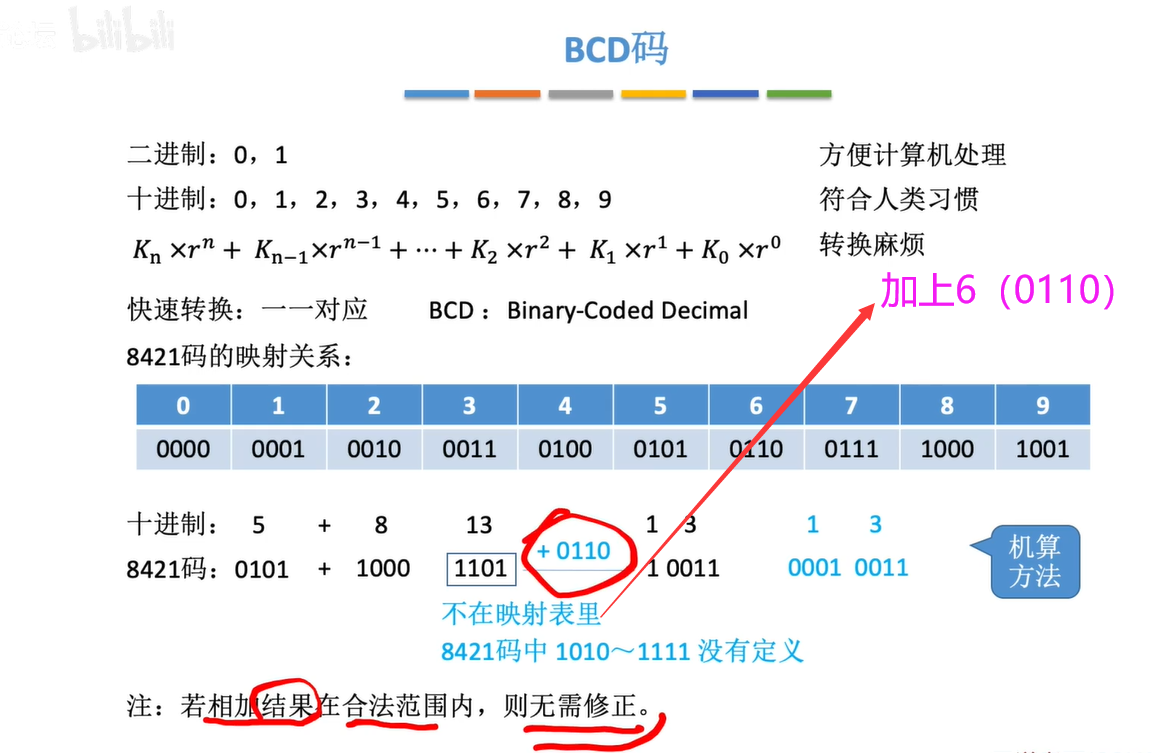
8421码的加法
1.2.2余3码

余3码的加法 相加后每位再加上3(0011)
例 5+8=13 1000+1011=1 0011 1 +0011=0100 0011+0011=0110 即 0100 0110=13
1.2.3 2421码
改变权值定义

0-4 编码的第一位必须是0
5之后 编码的第一位必须是1 防止 歧义 例 5 =2+2+1=4+1 1011 0101
1.2.4小结
1.3 字符与字符串
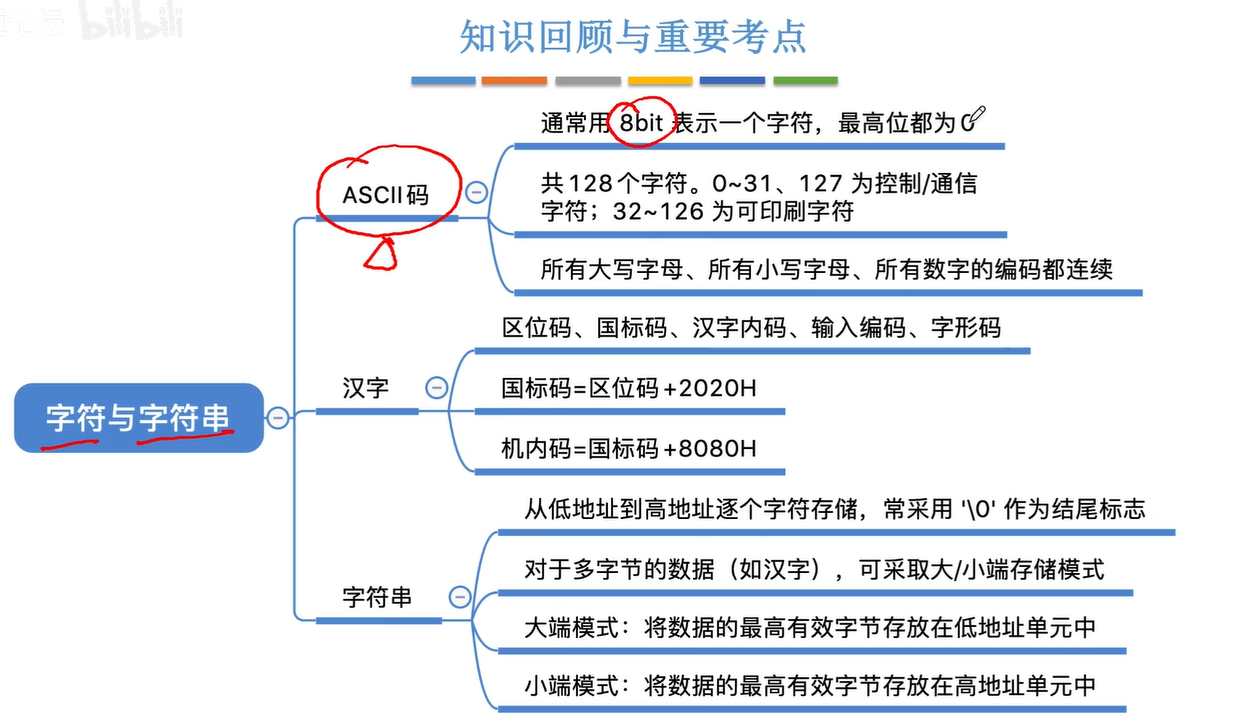
1.3.1ASCII码
常用的字符 共128个 故需要7个二进制编码
但是存入计算机的时候 通常要在最高位 补一个0 凑够一个字节
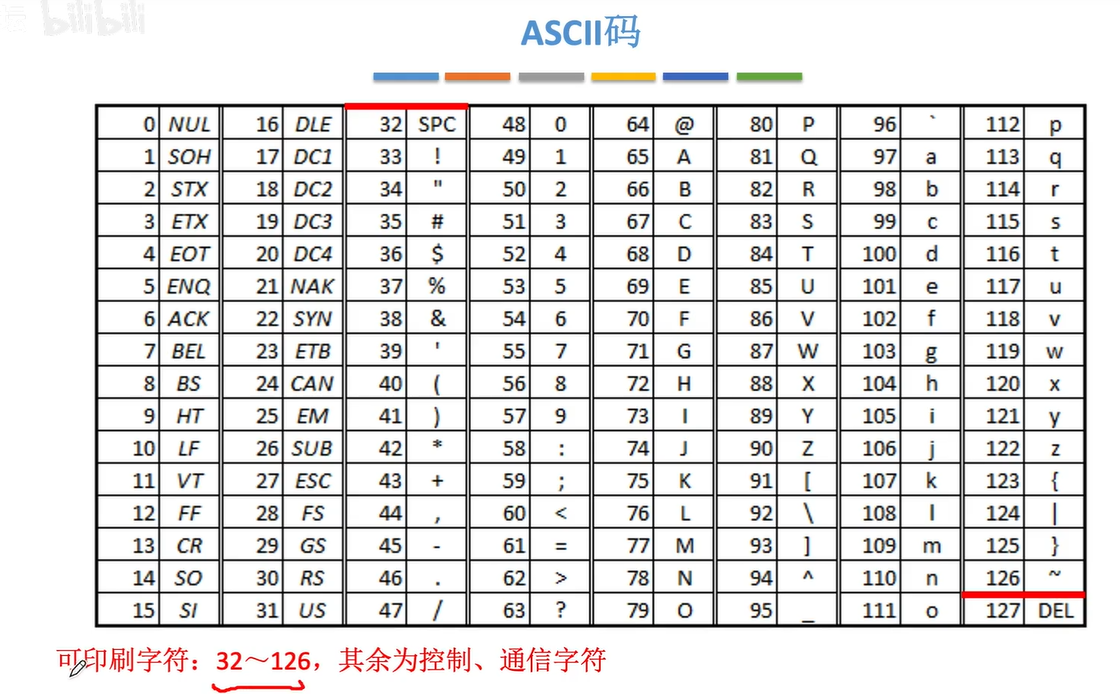
特别的在 48-57位上 表示0-9
48(0011 0000)~57(0011 1001) 后四位就是0-9数字对应的8421码
字母 前三位相同 后五位就是 1(0 0001)--26(1 1010)

65+32=97 大写+32=小写
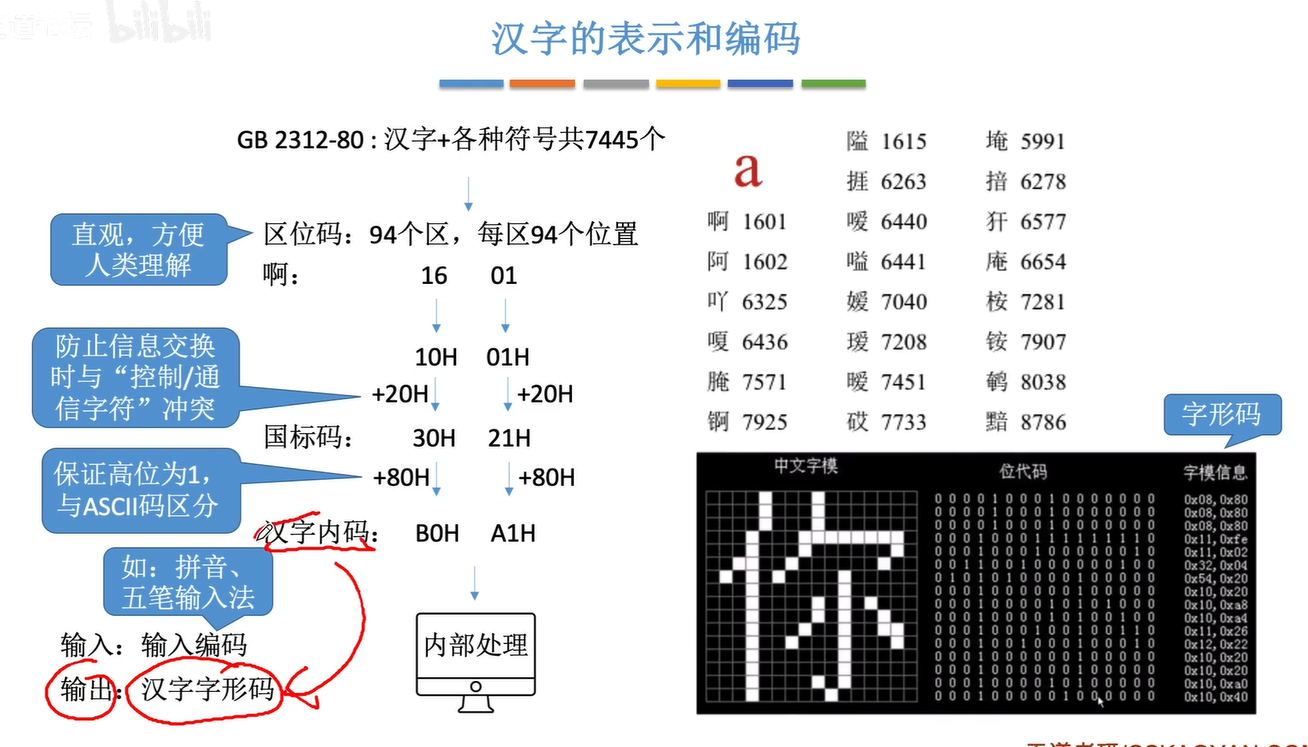
1.3.2汉字表示及编码
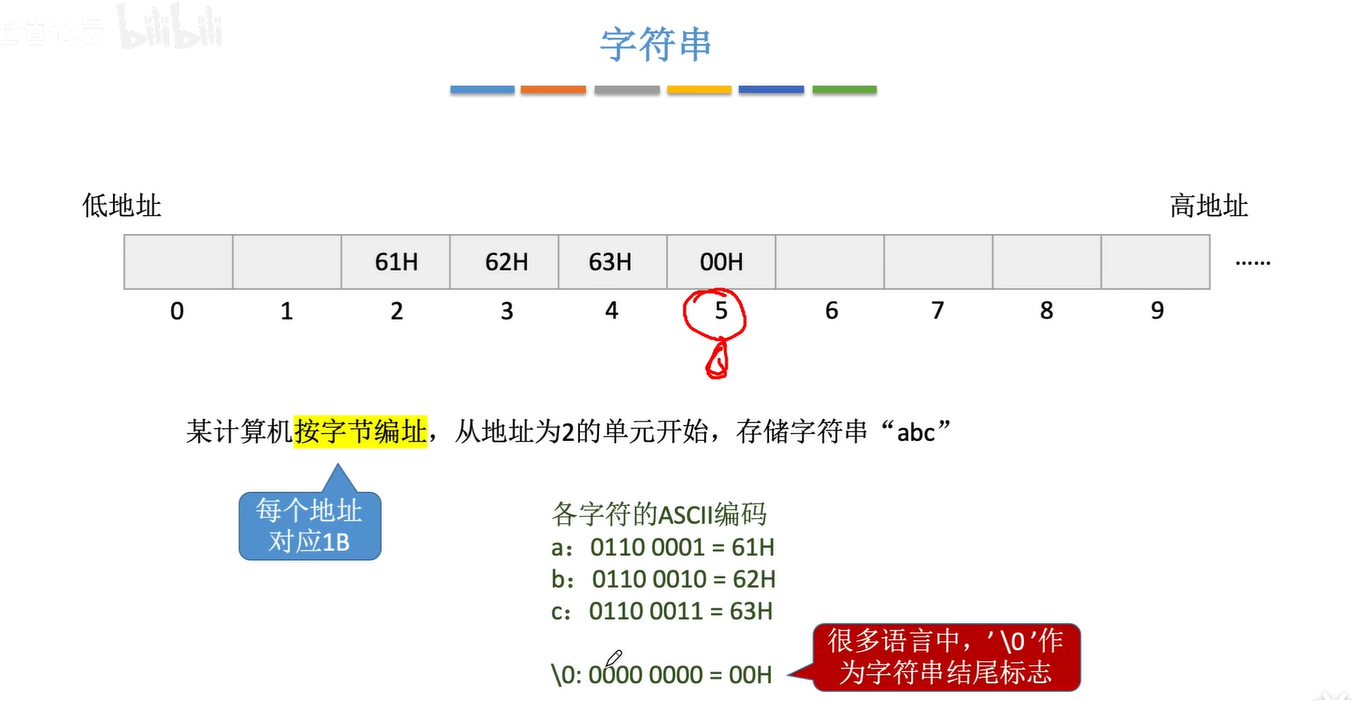
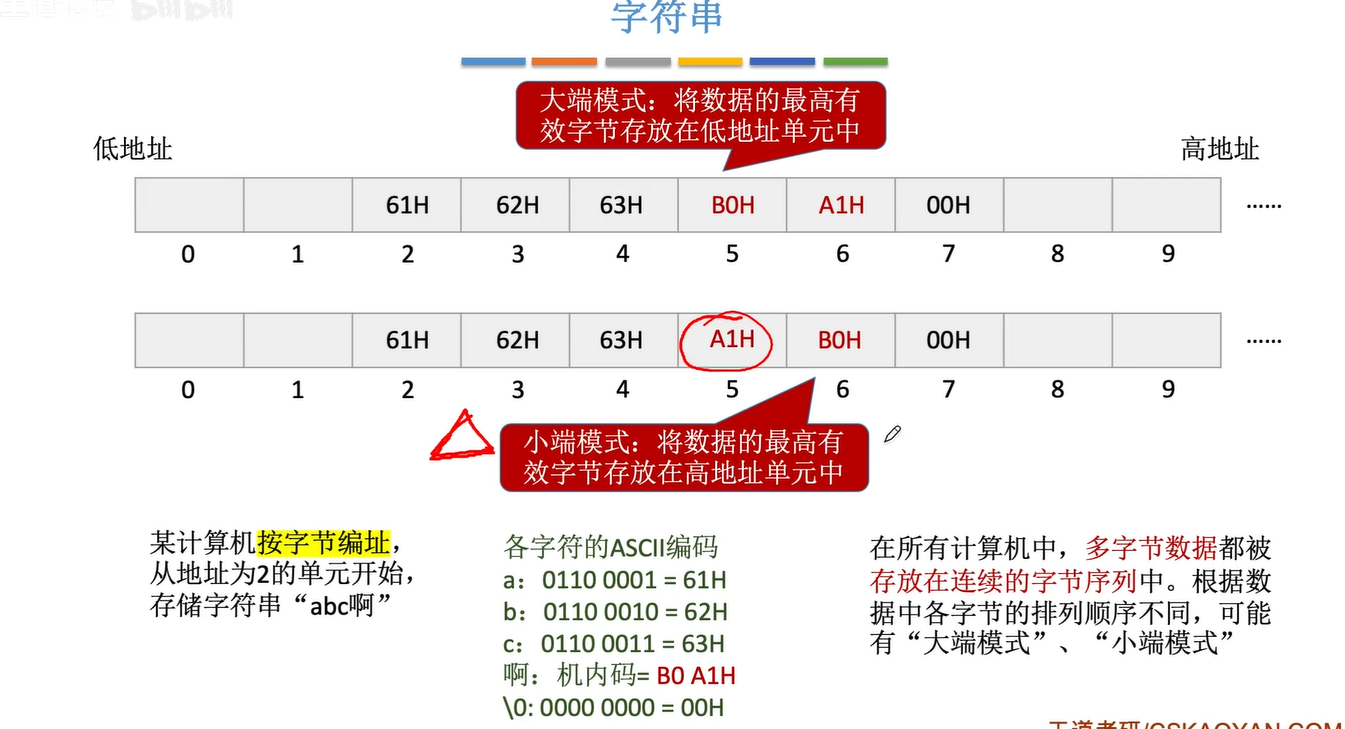
1.3.3字符串
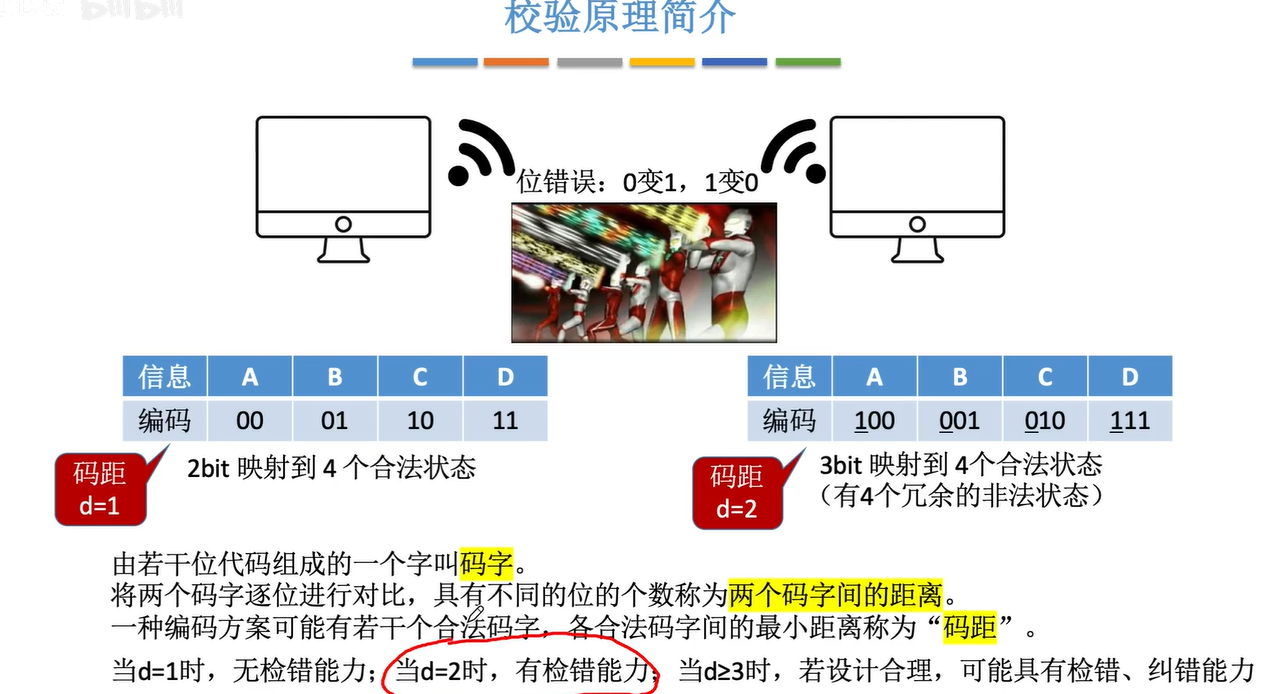
1.4奇偶校验码
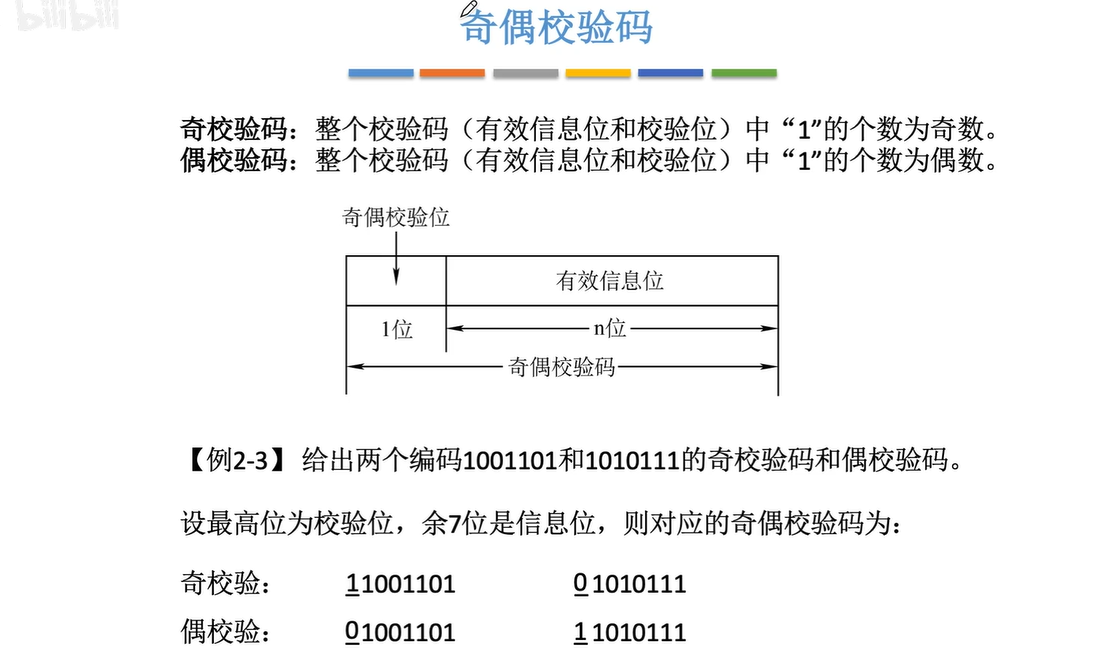
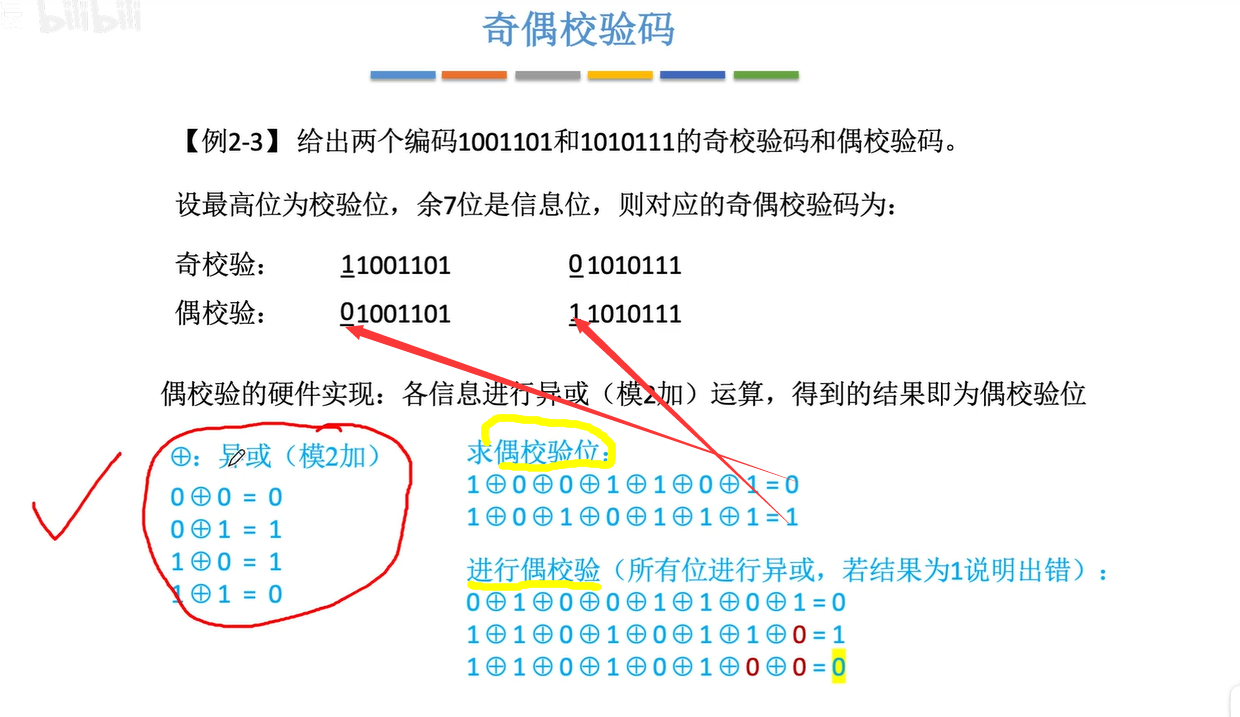
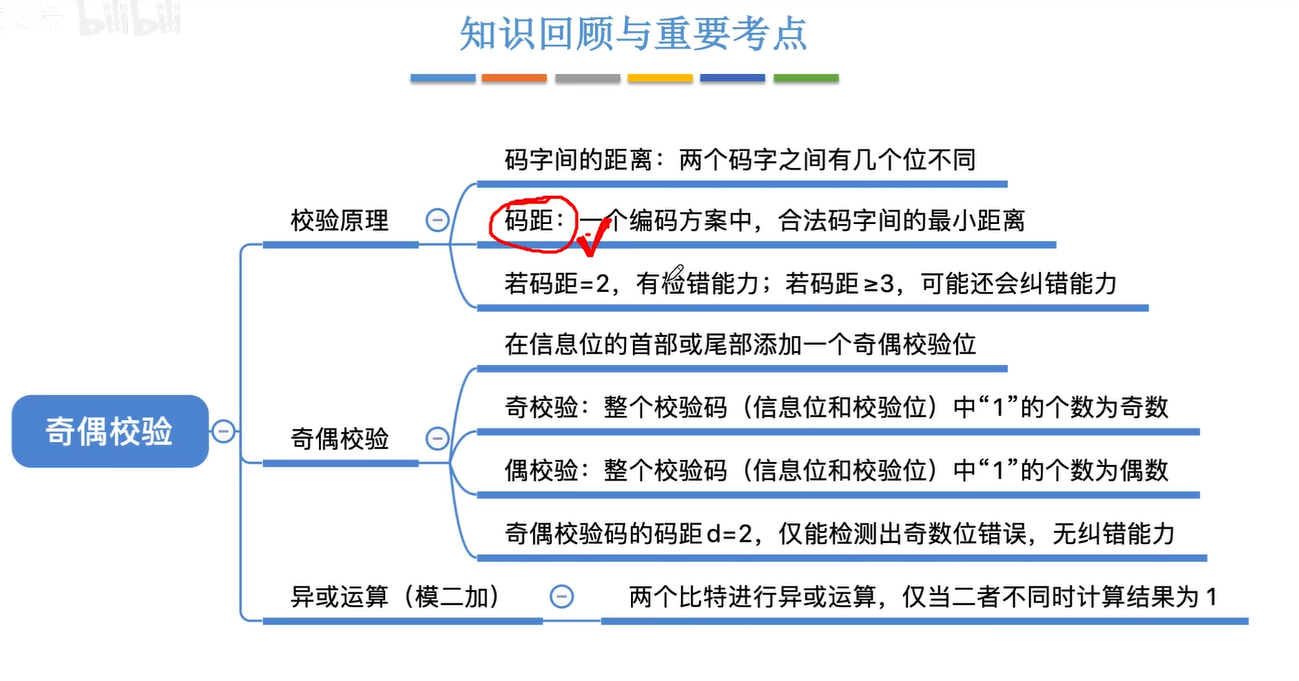
1.5海明码
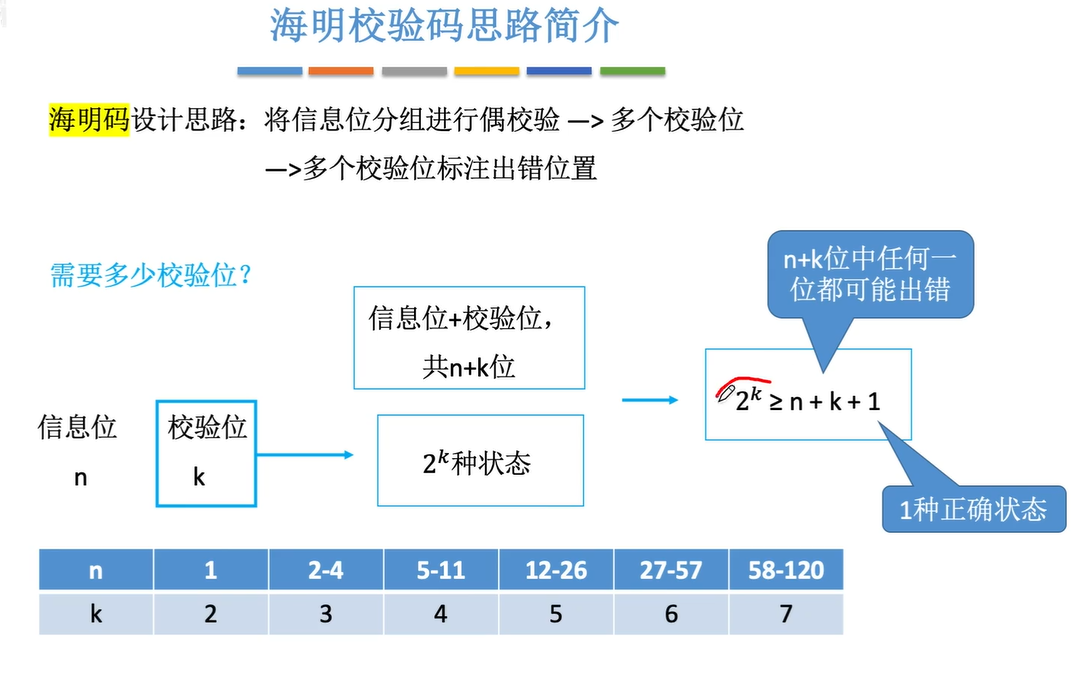

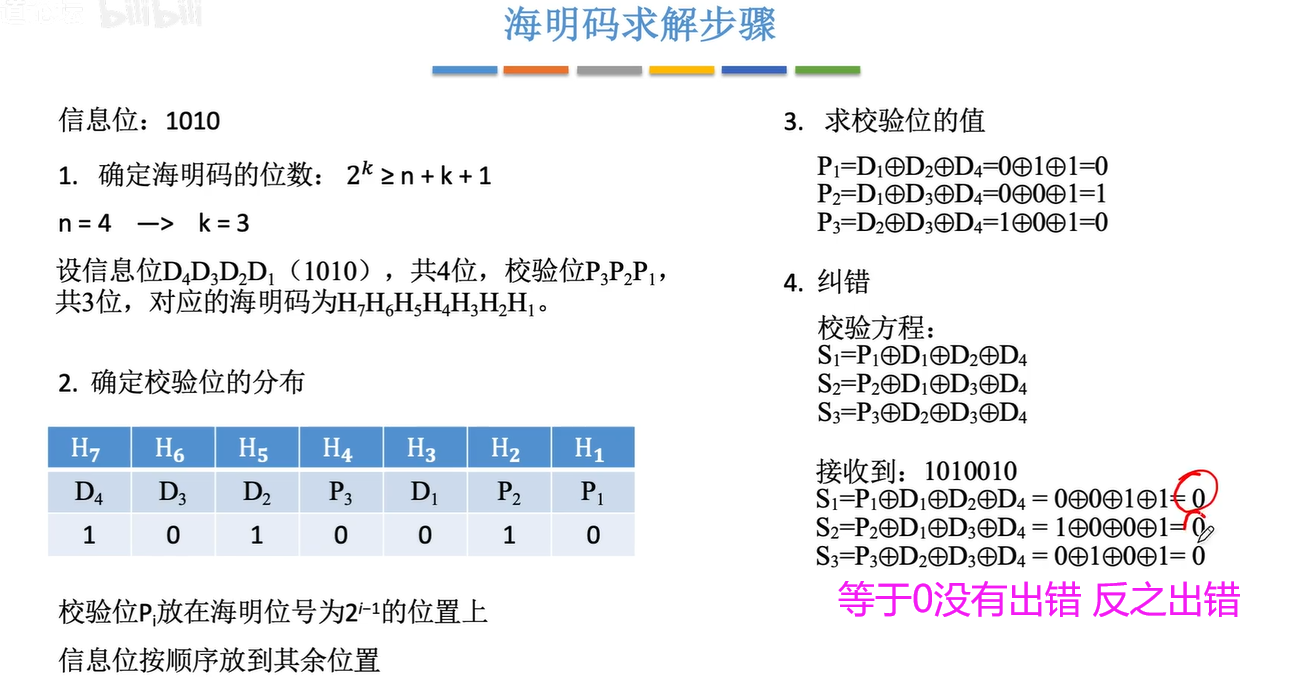
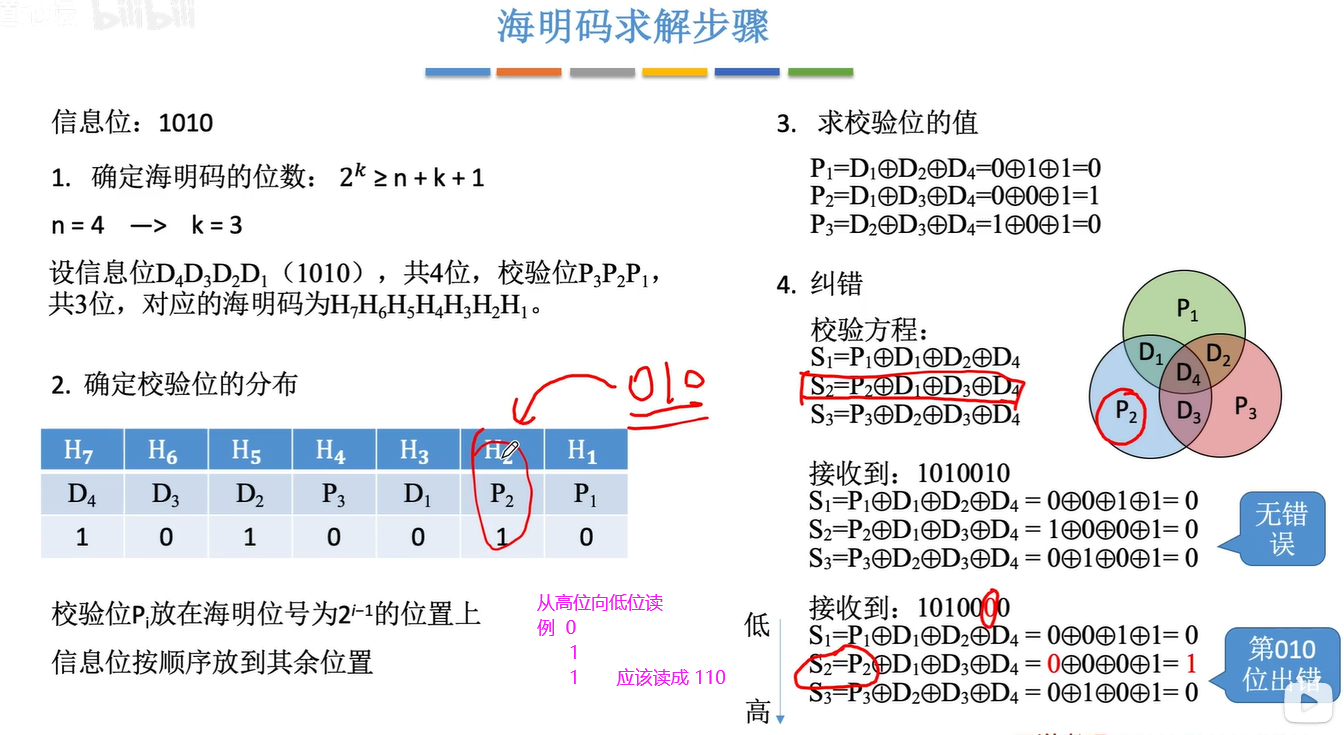
题目格式可能不一样
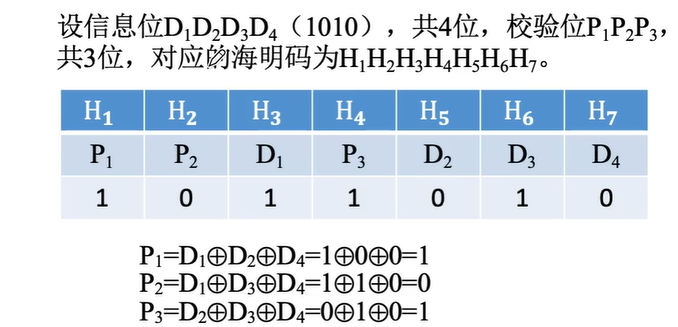
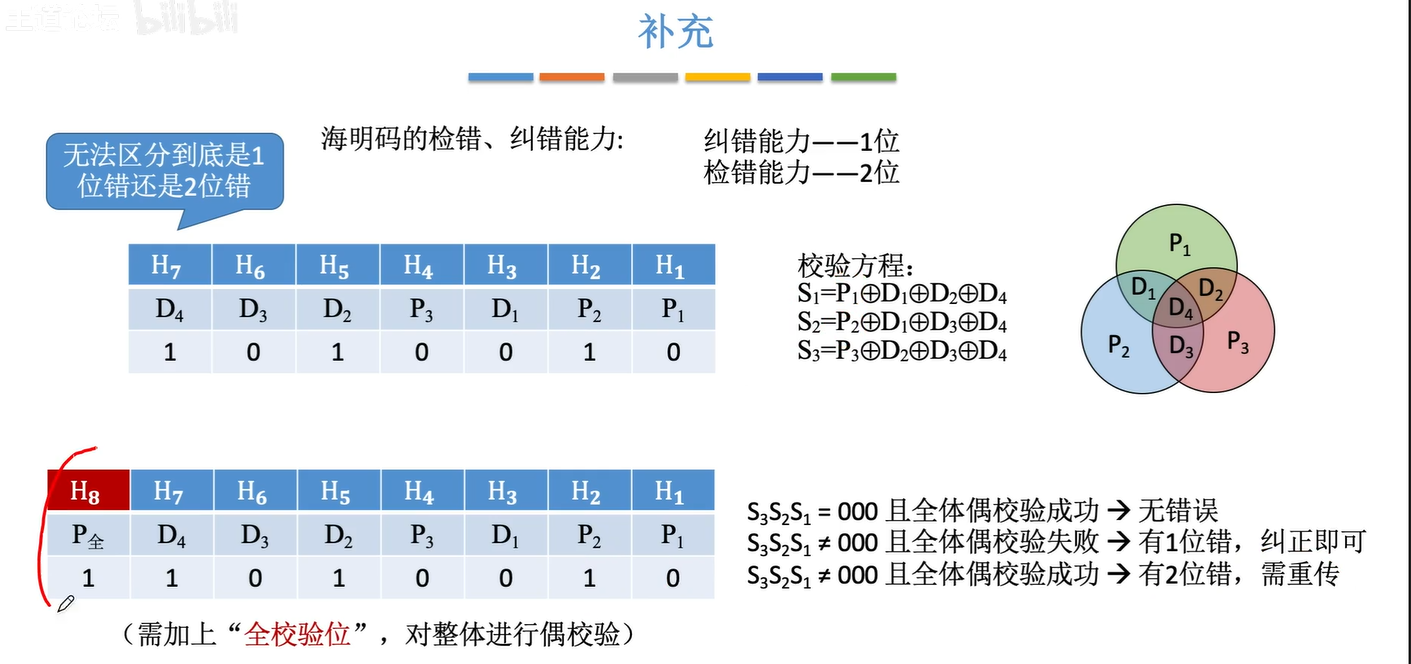
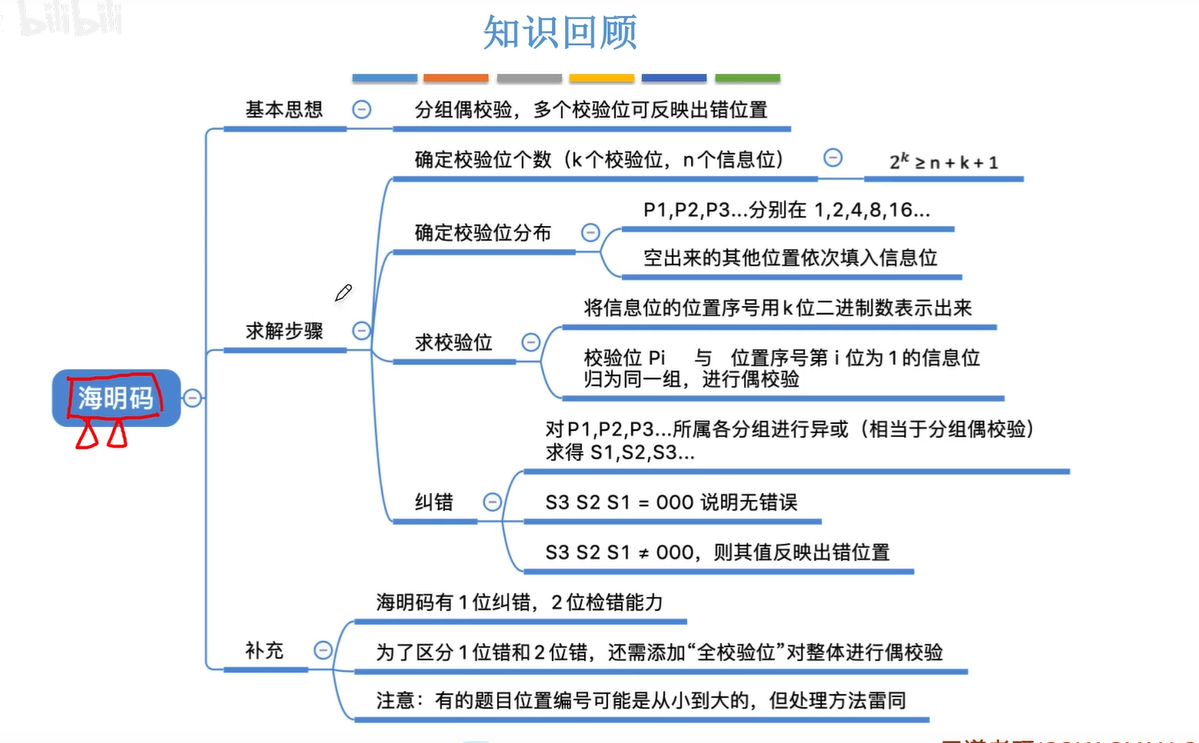
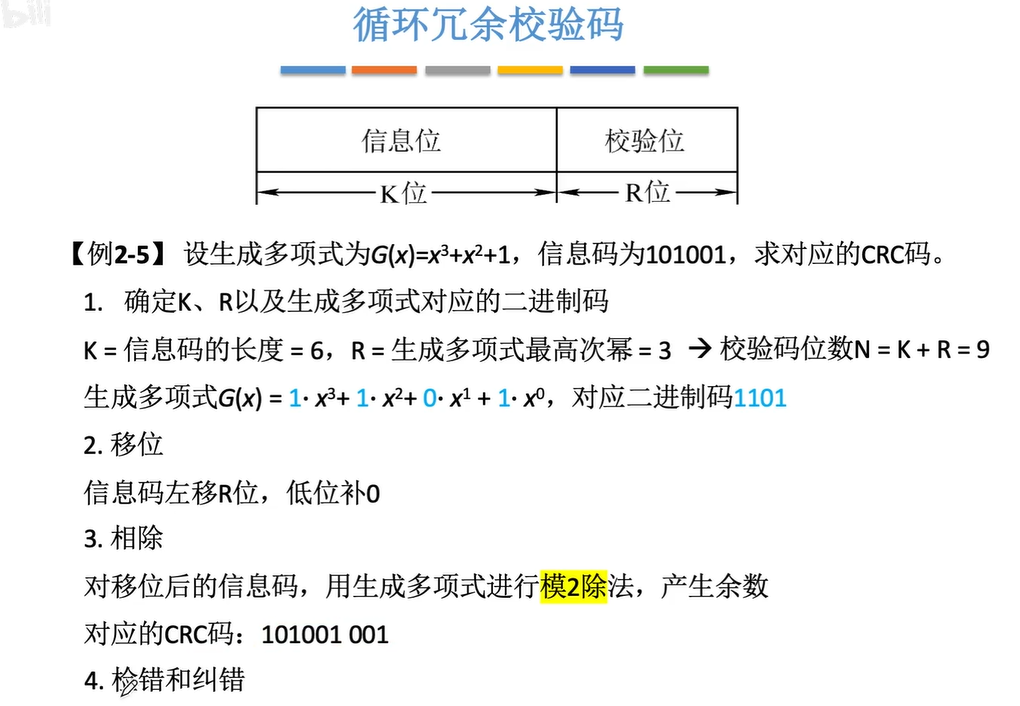
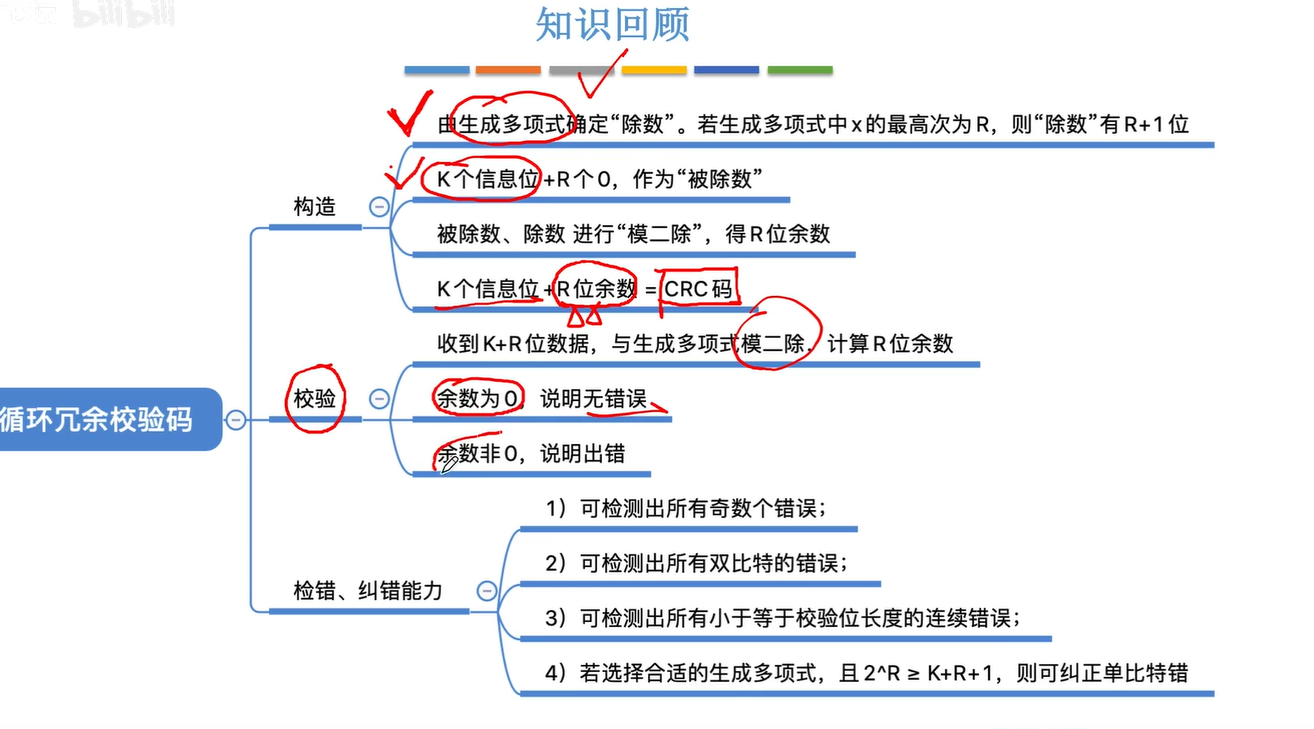
1.6循环冗余校验码
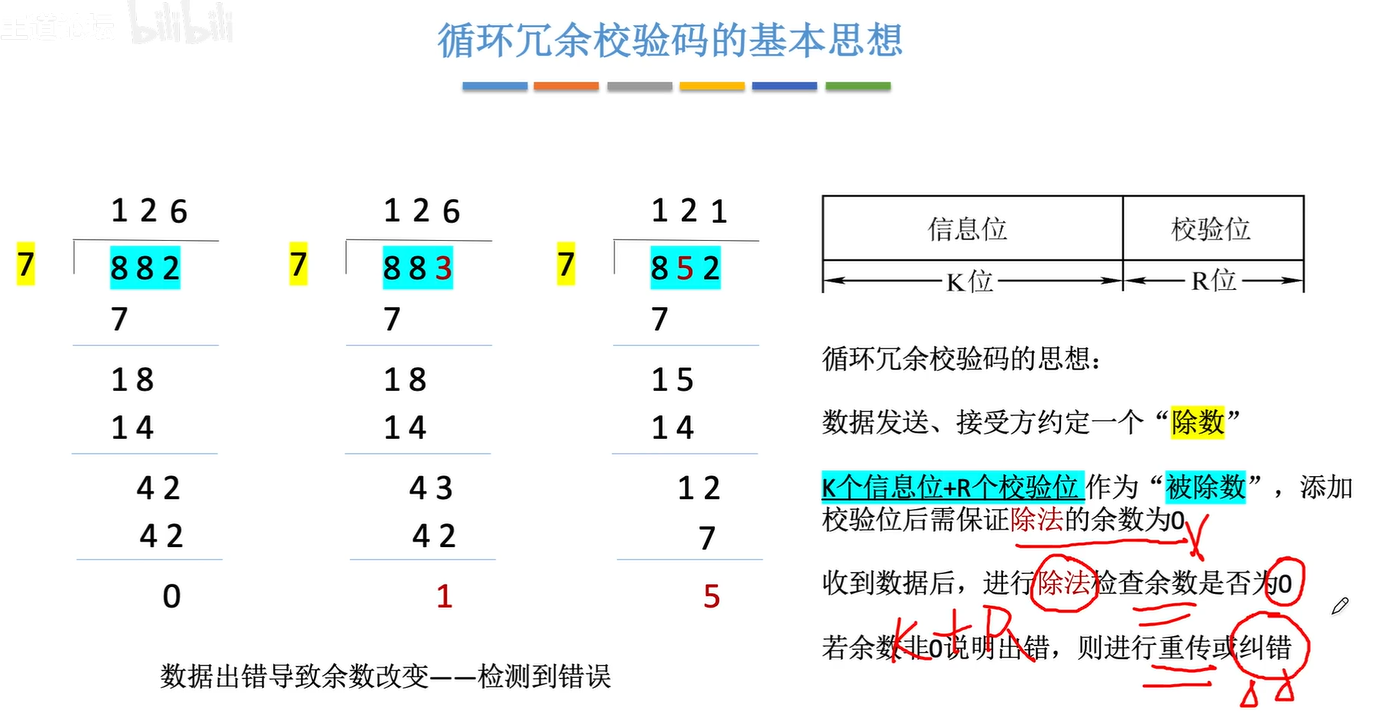
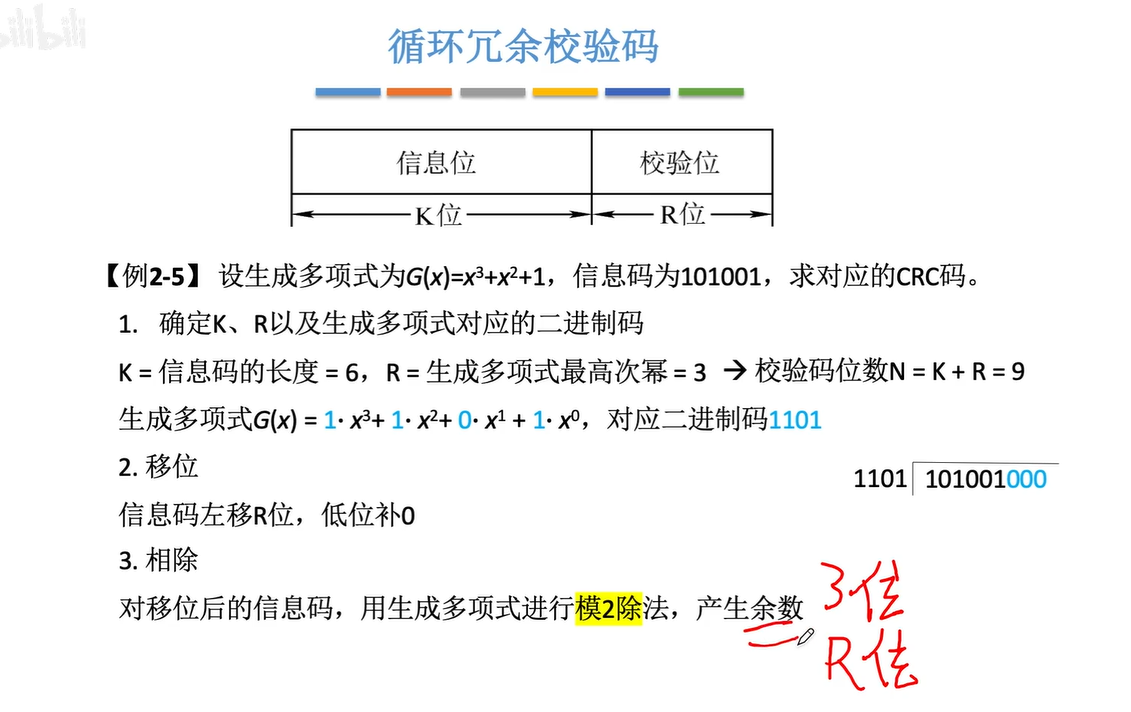
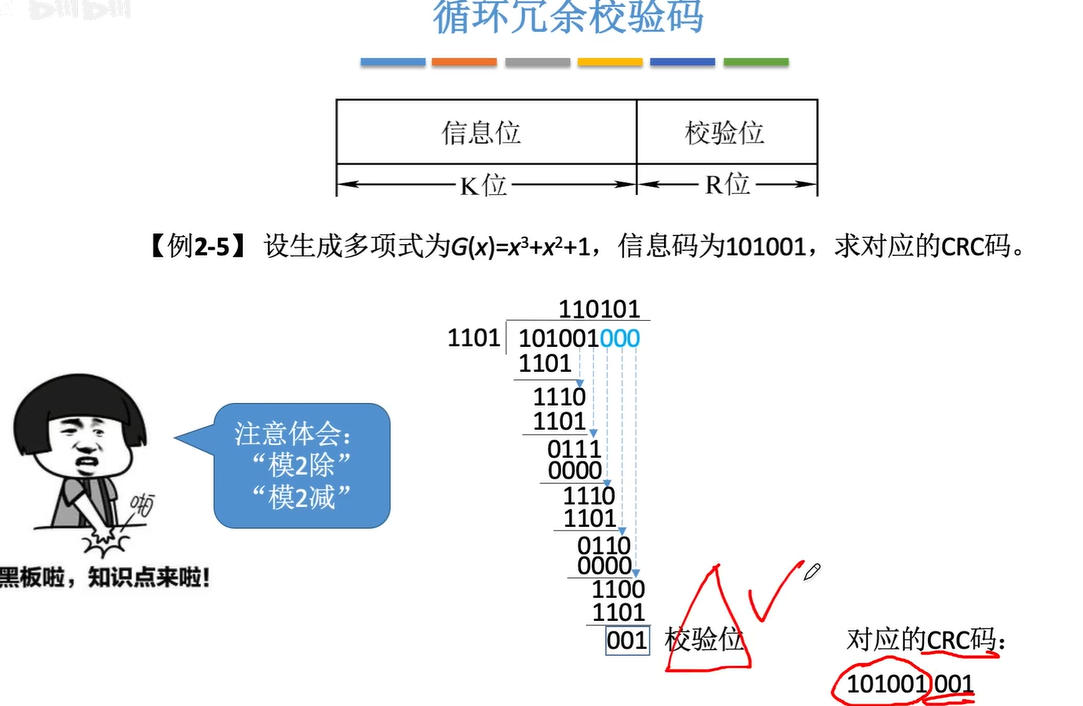
模2除就是异或
模2减:(就结果而言 和 异或一样 如下:)
0-0=0
1-1=0
1-0=1
0-1=1

2.1定点数

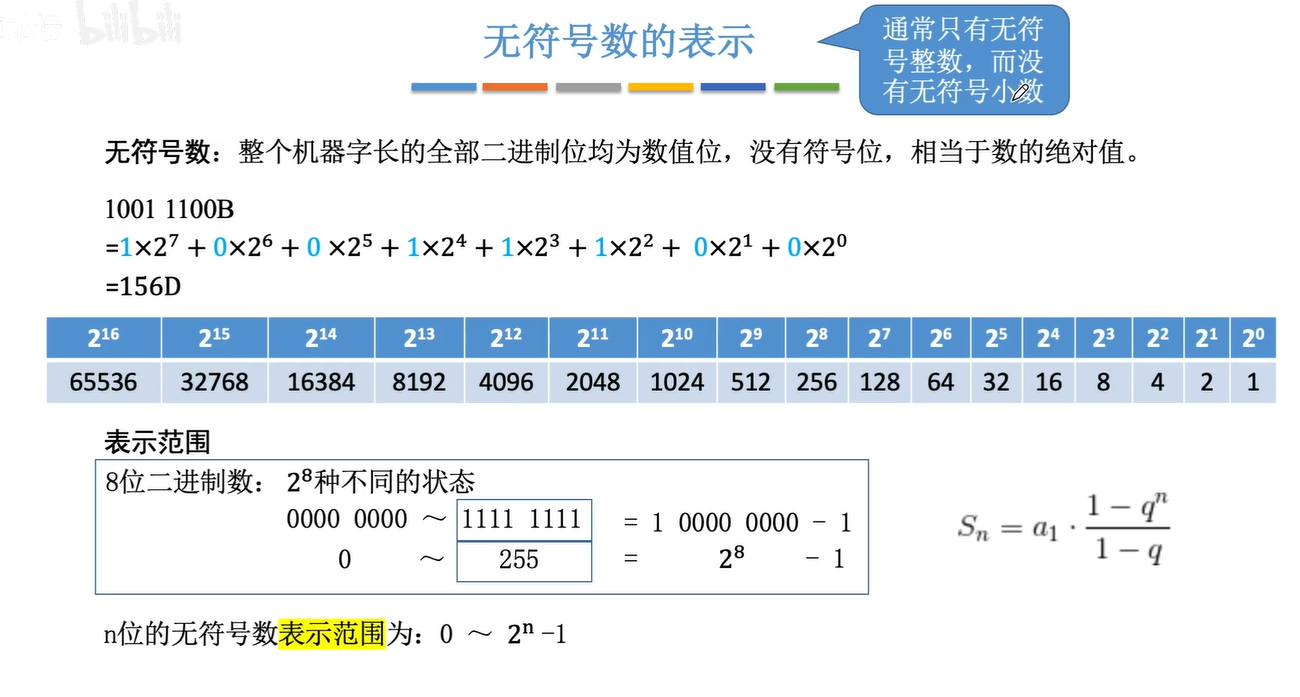
2.1.1无符号数
2.1.2有符号数
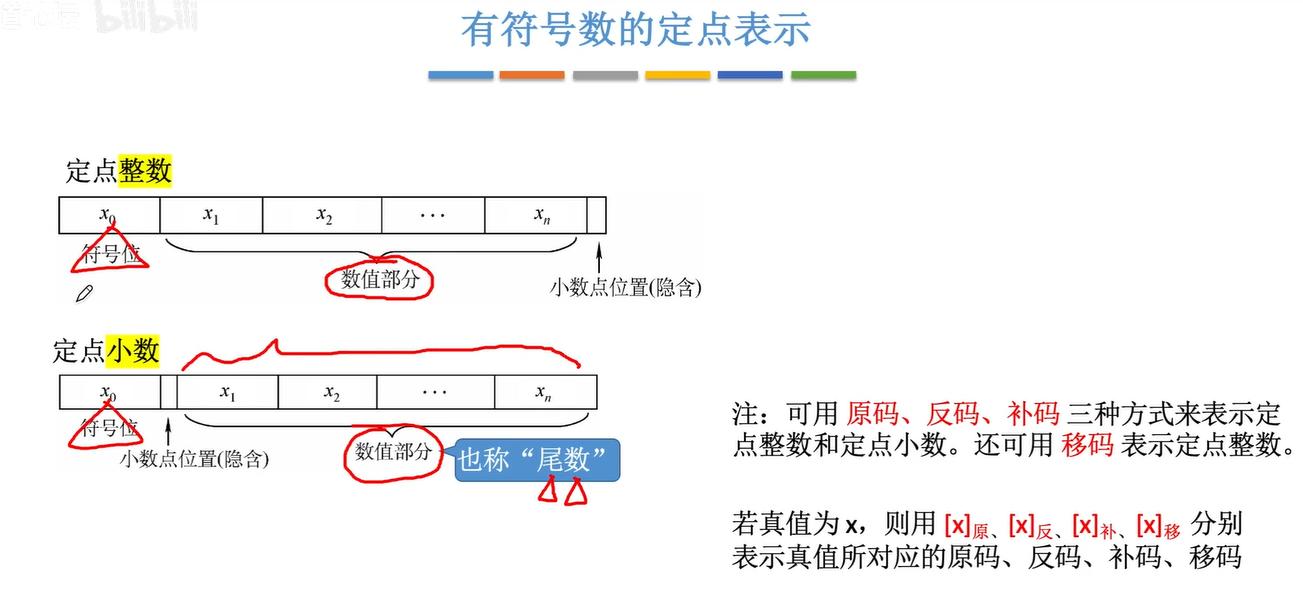
原码
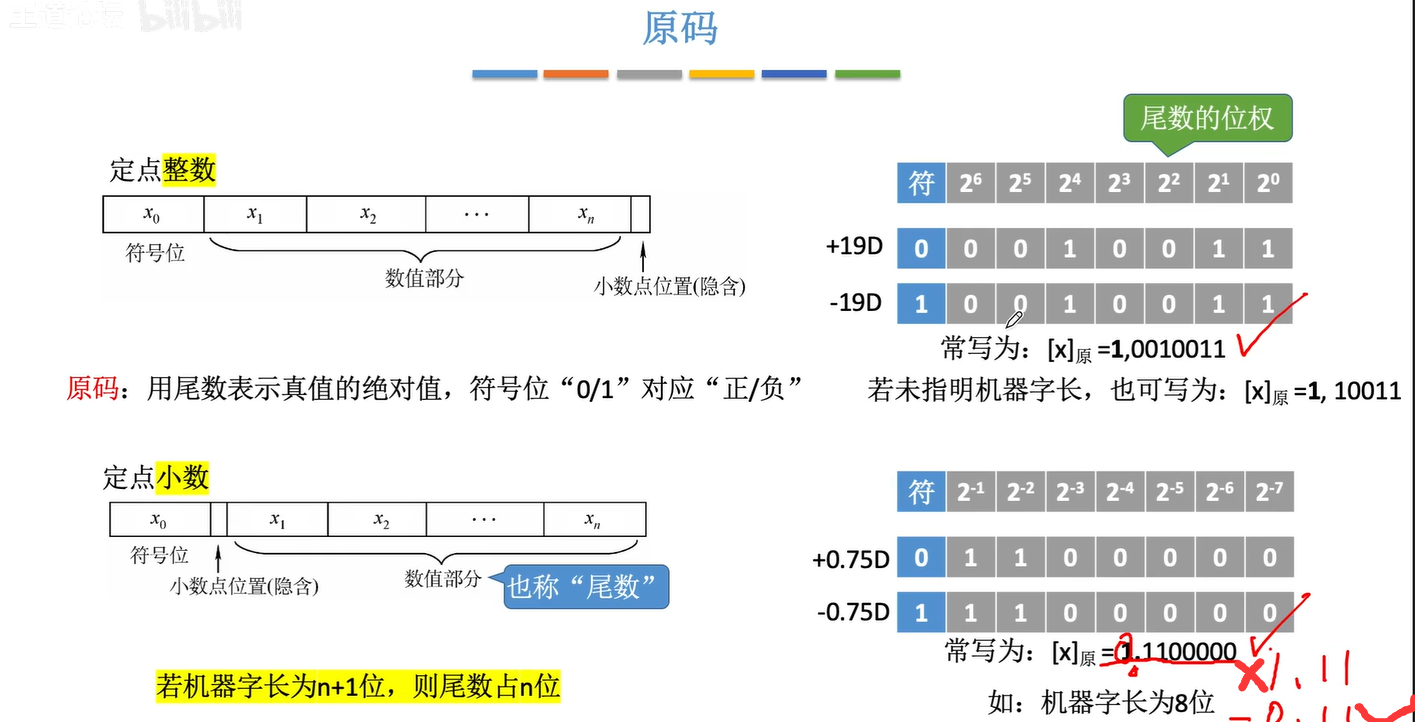
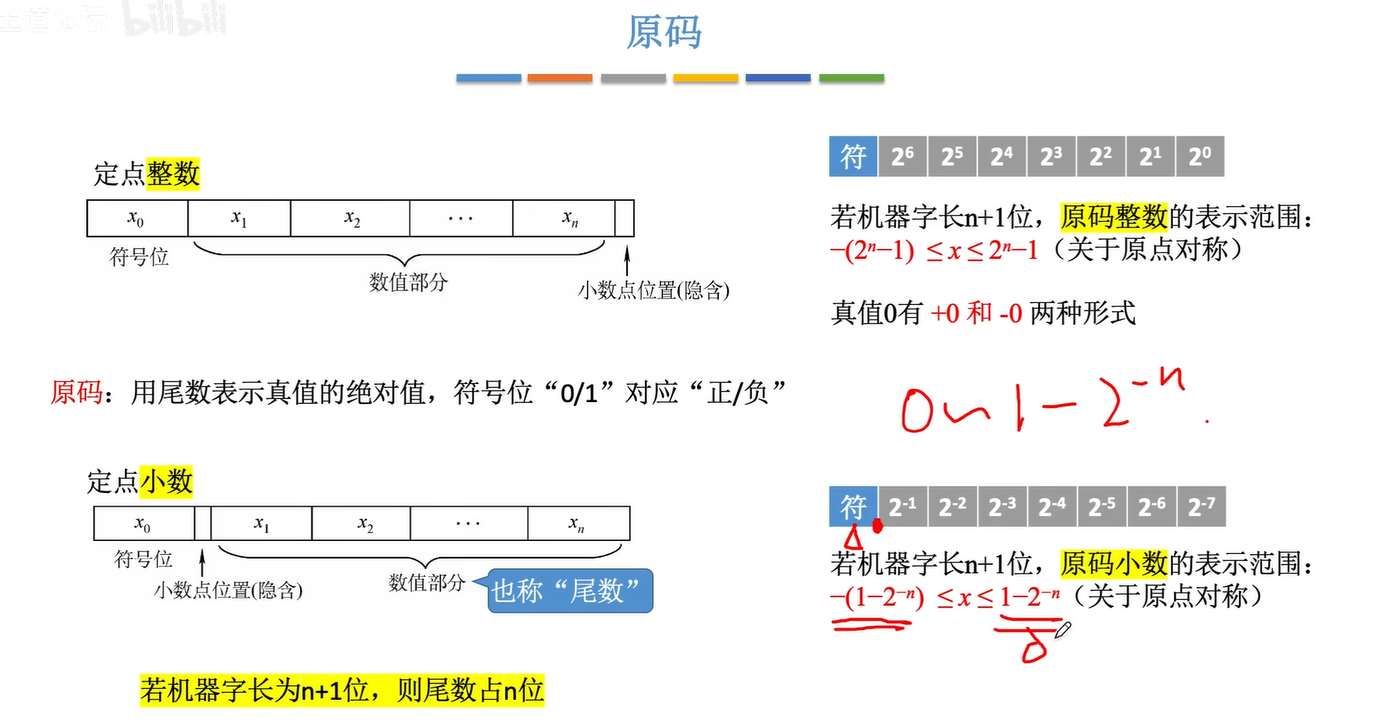
原码范围
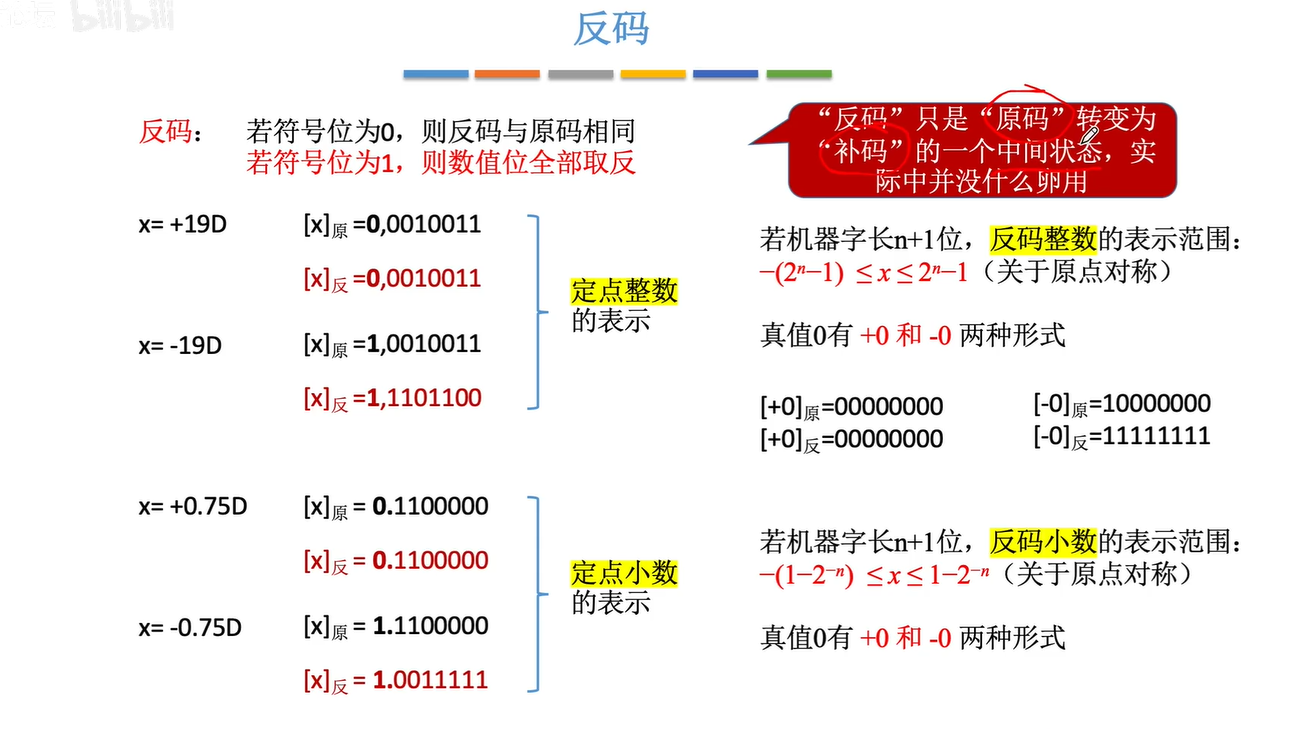
反码
补码
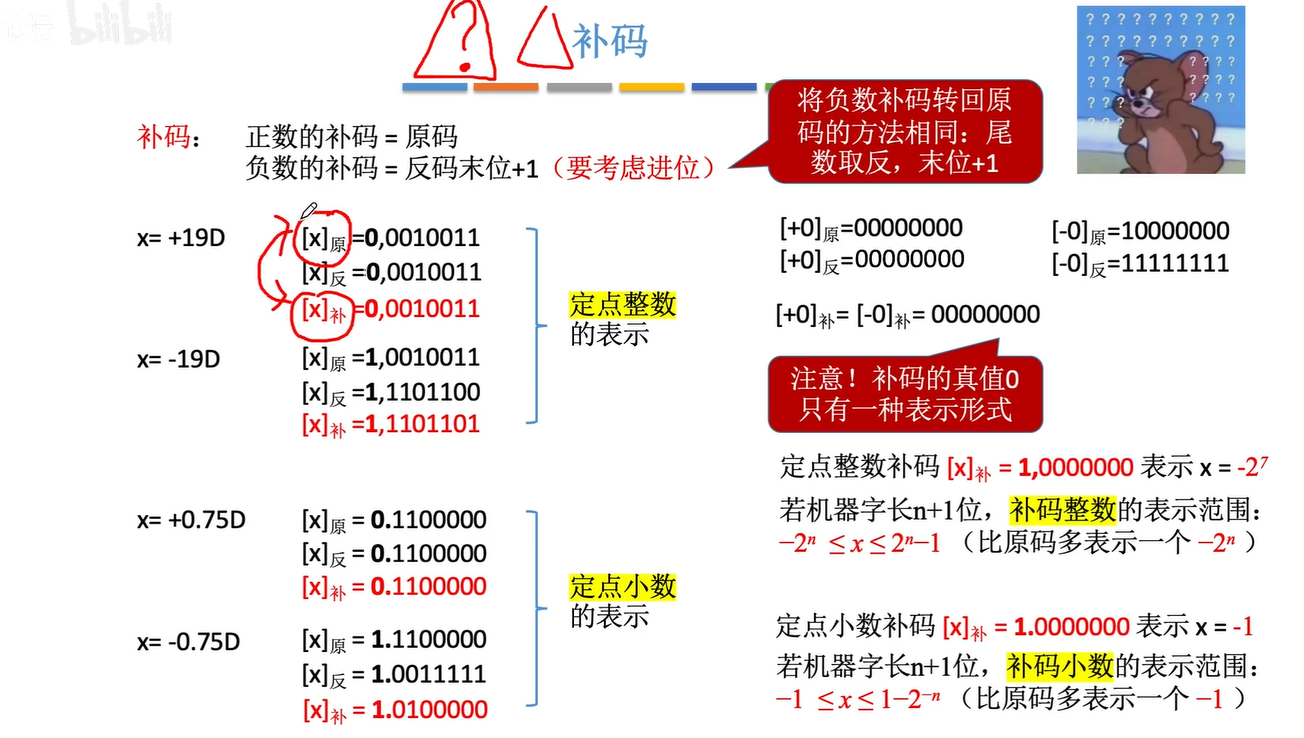
补码转源码 取反加一
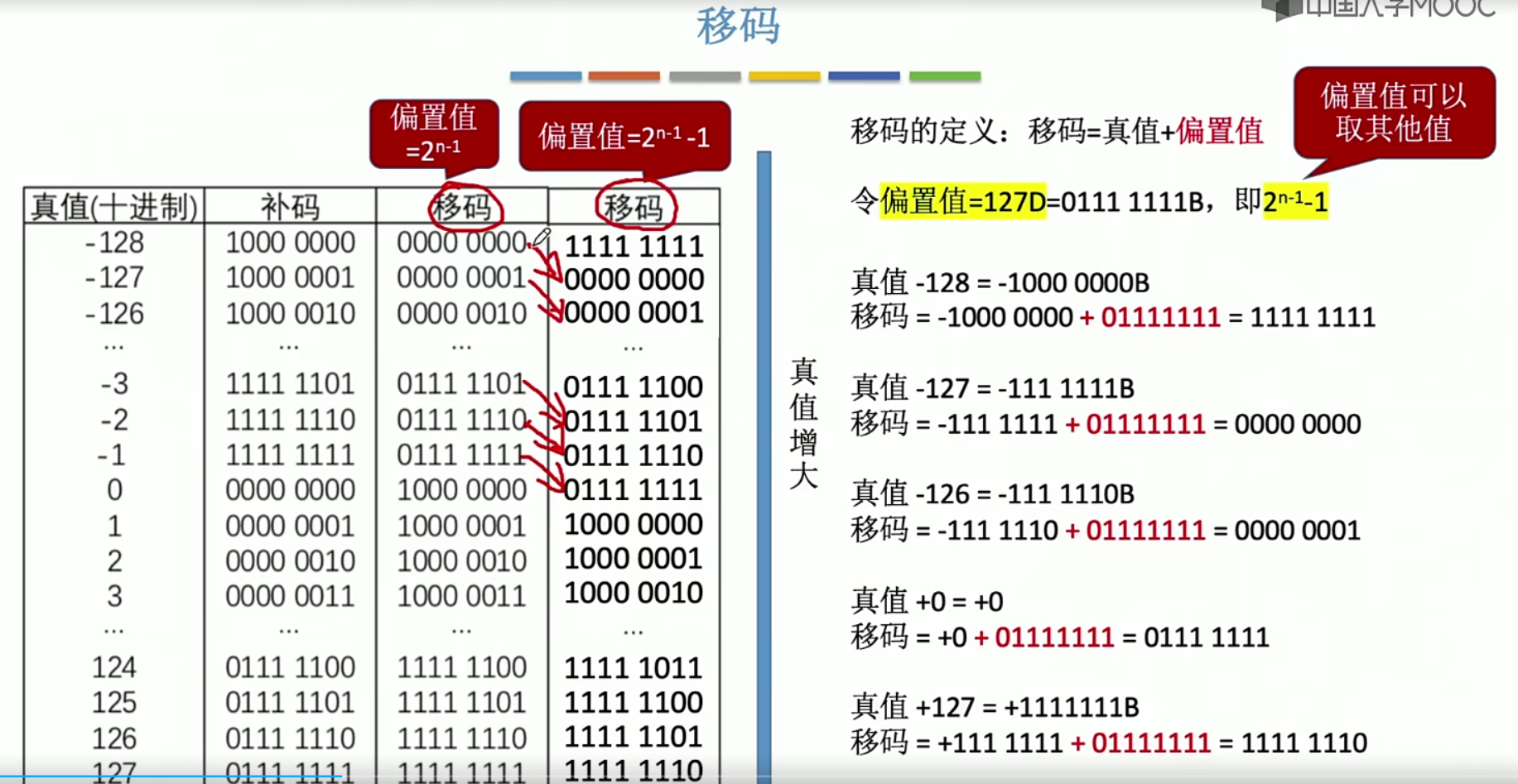
移码
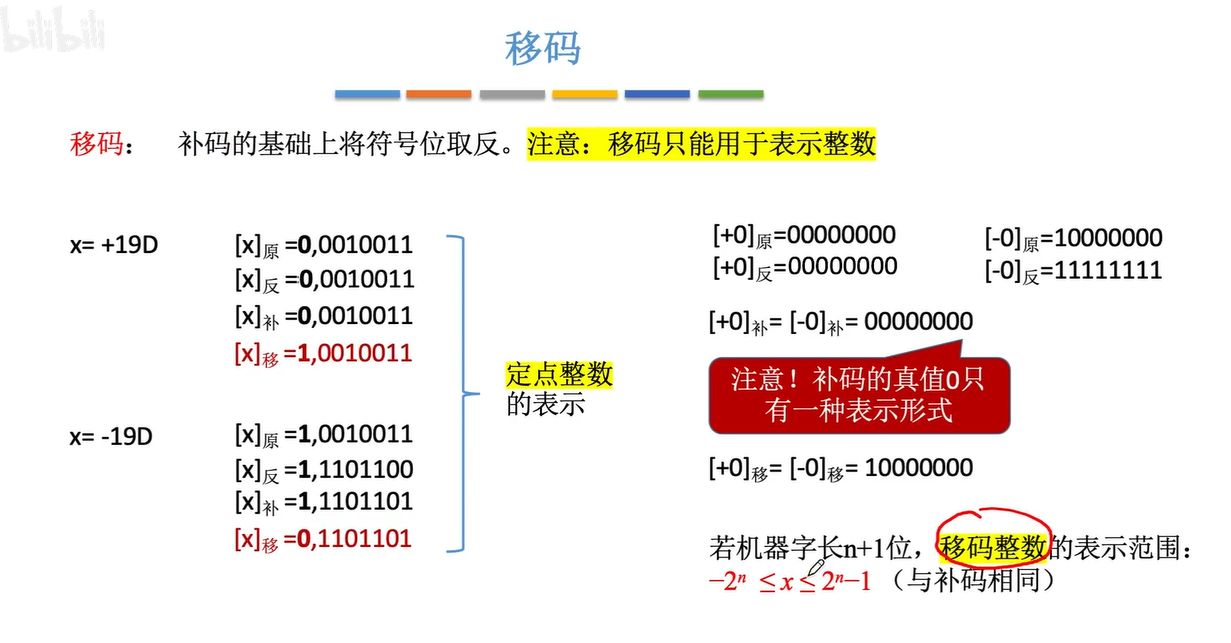
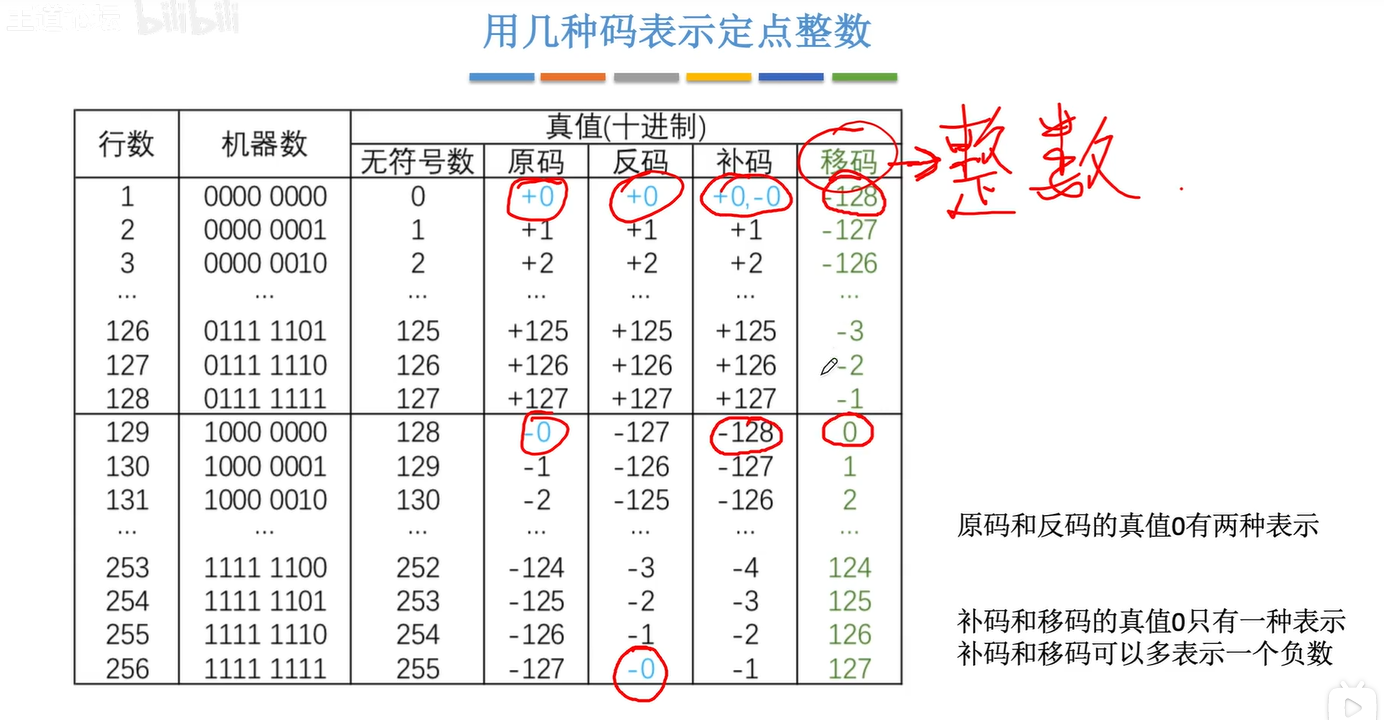
几种码
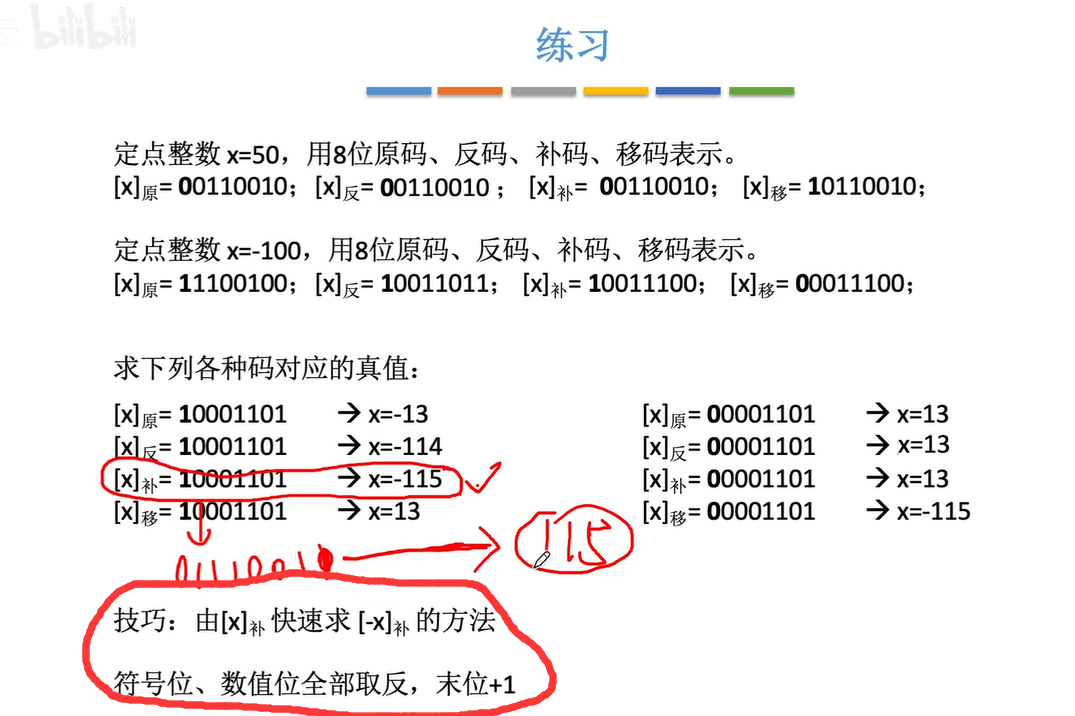
练习
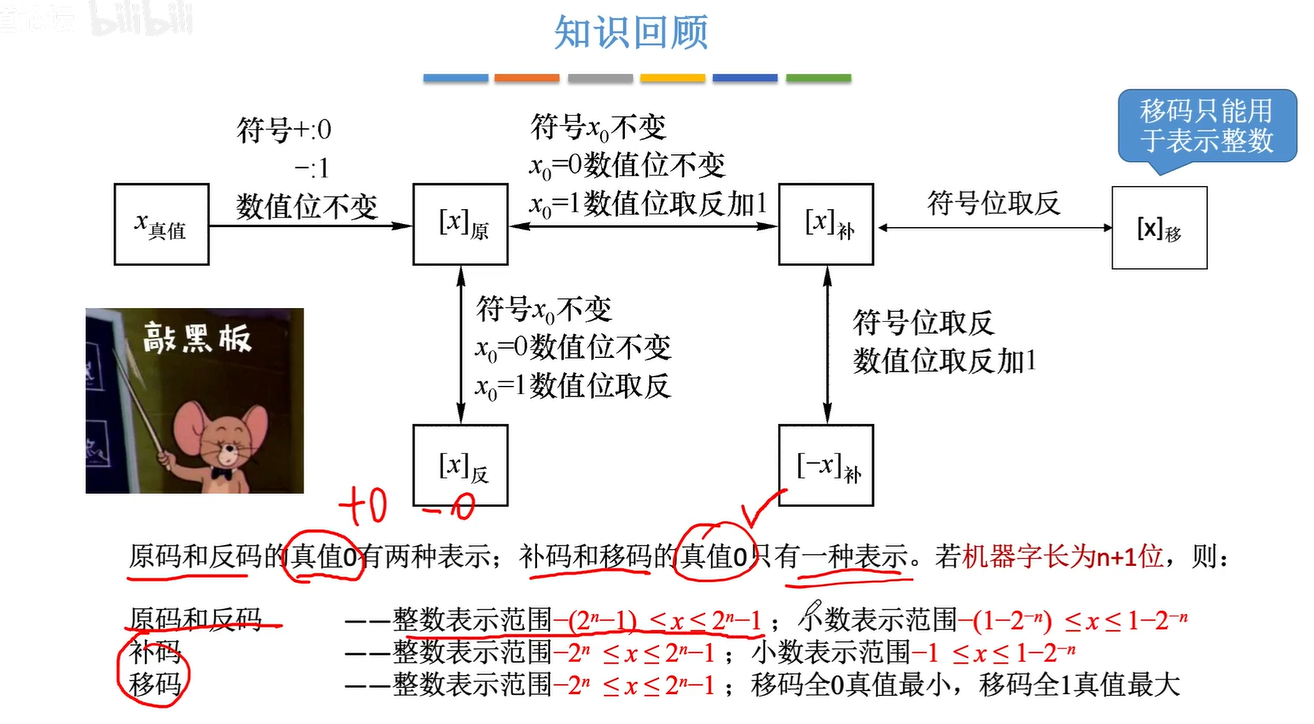
小结
2.2原码补码移码的作用
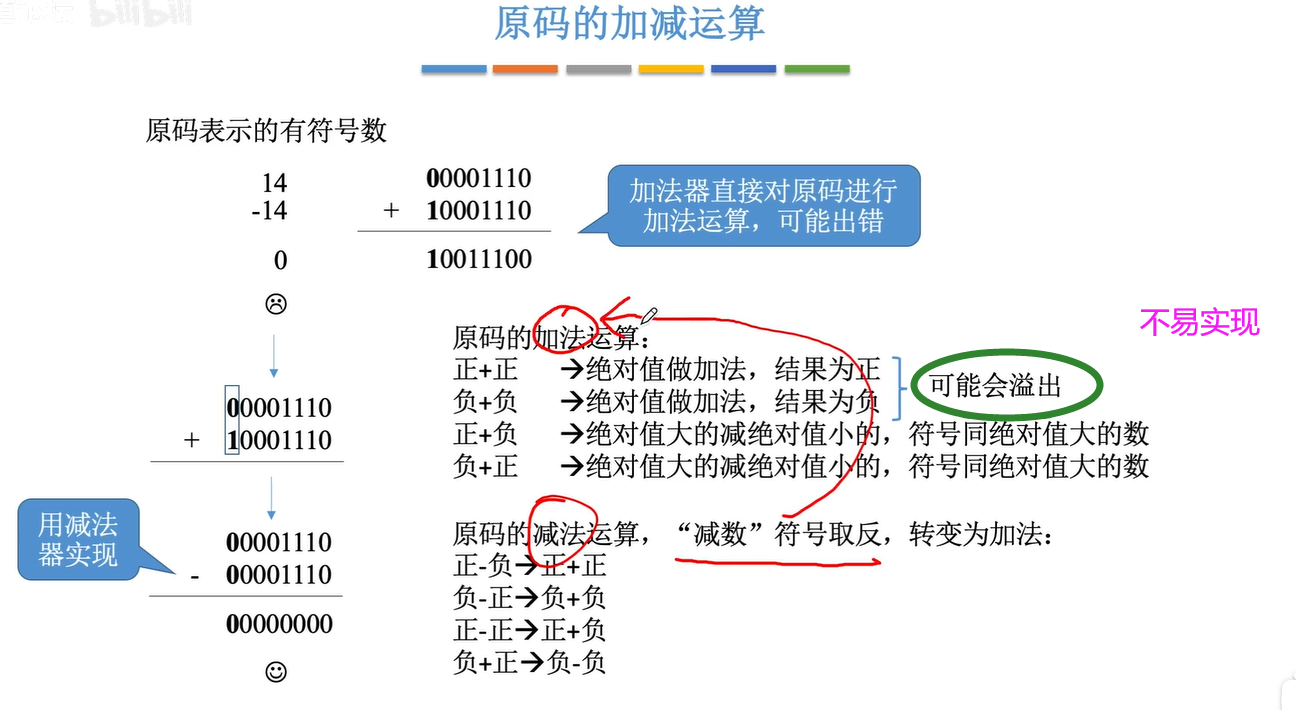
2.2.1原码的作用
进行加法运算

但是当进行有符号数之间的加法时,会出现错误。

结果非0,所以便引入补码。
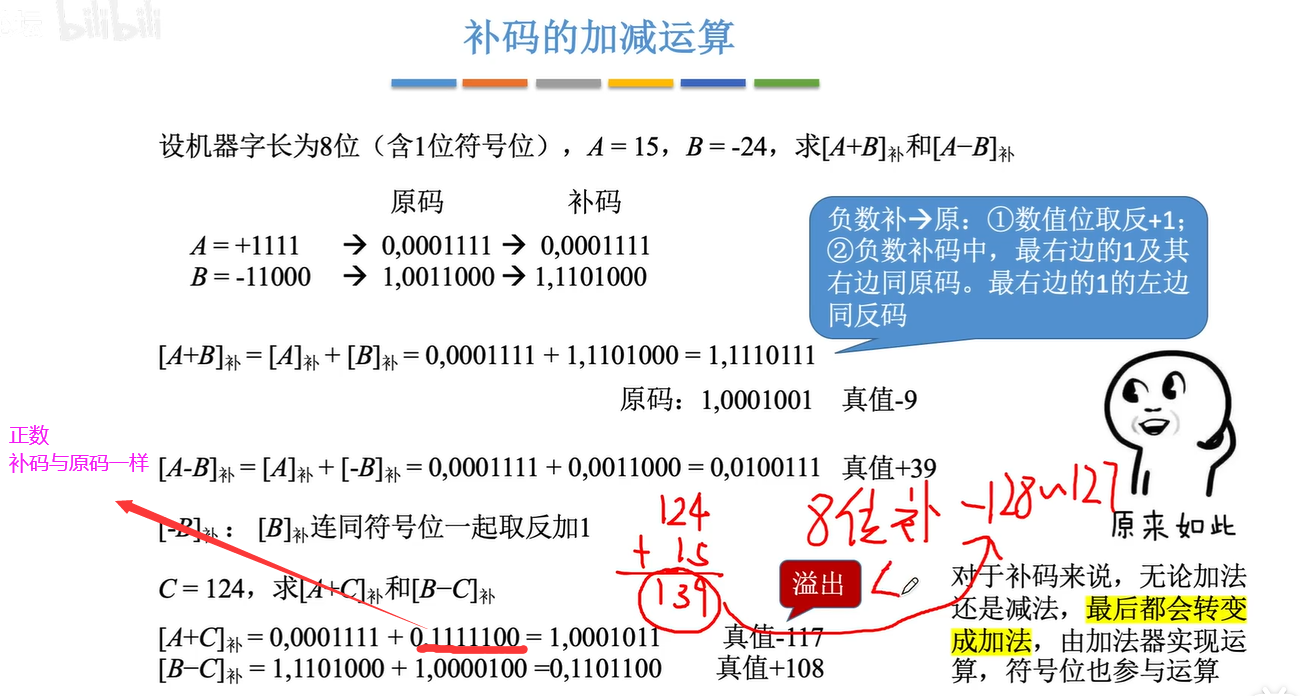
2.2.2 补码的作用
补码是为了让减法操作变为加法操作,减少硬件的成本。
正数的补码为其本身,负数的补码为符号位不变,其余位取反加一。
(如何理解补码?
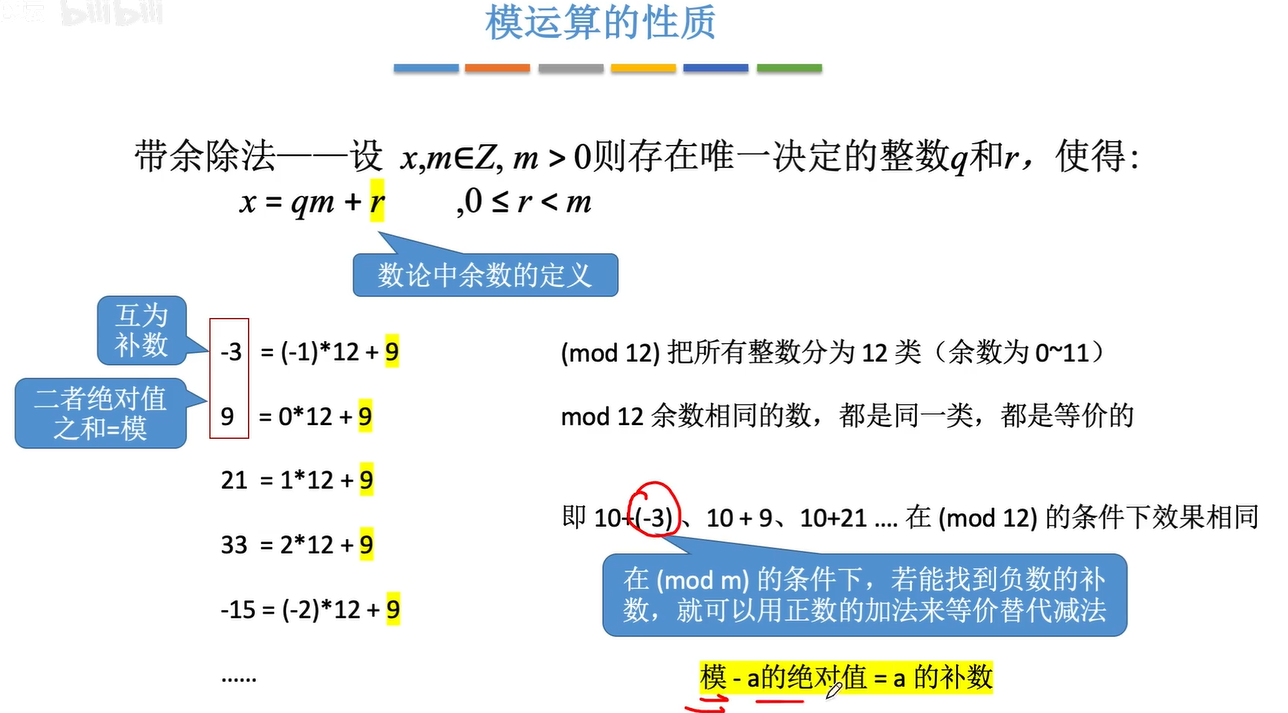
以时钟举例,现在是10点,想要变为3点,可以顺时针旋转5格,记为+5;也可以逆时针旋转7格,记为-7。在此运算里面模为12,5mod12和-7mod12所对应的意义相同,都是将10点变为3点。
由此可以看到,在计算机中,记一个字长为8bit,所以大小为00000000~11111111,由此可以理解模为2^8。
公式:模-a的绝对值=a的补码(a为负数)
例如10001010(-18)的绝对值为00001010(18)
a的补码为反码加1,11110110(-18的补码)
由上述公式可得:
100000000=00001010+11110110
理解补码后,将减法变为加法例如18减去18等于18加上(-18),意义等同于加上-18的补码。
结果本应该为100000000,但是只有8位存储,所以去掉最高位1,结果为00000000。)
例子:
48-19=48+(-19)
-19的补码为11101101

去掉最高位得00011101(29)
模运算的性质
2.2.3移码的作用
对计算机而言 移码更方便比较真值的大小

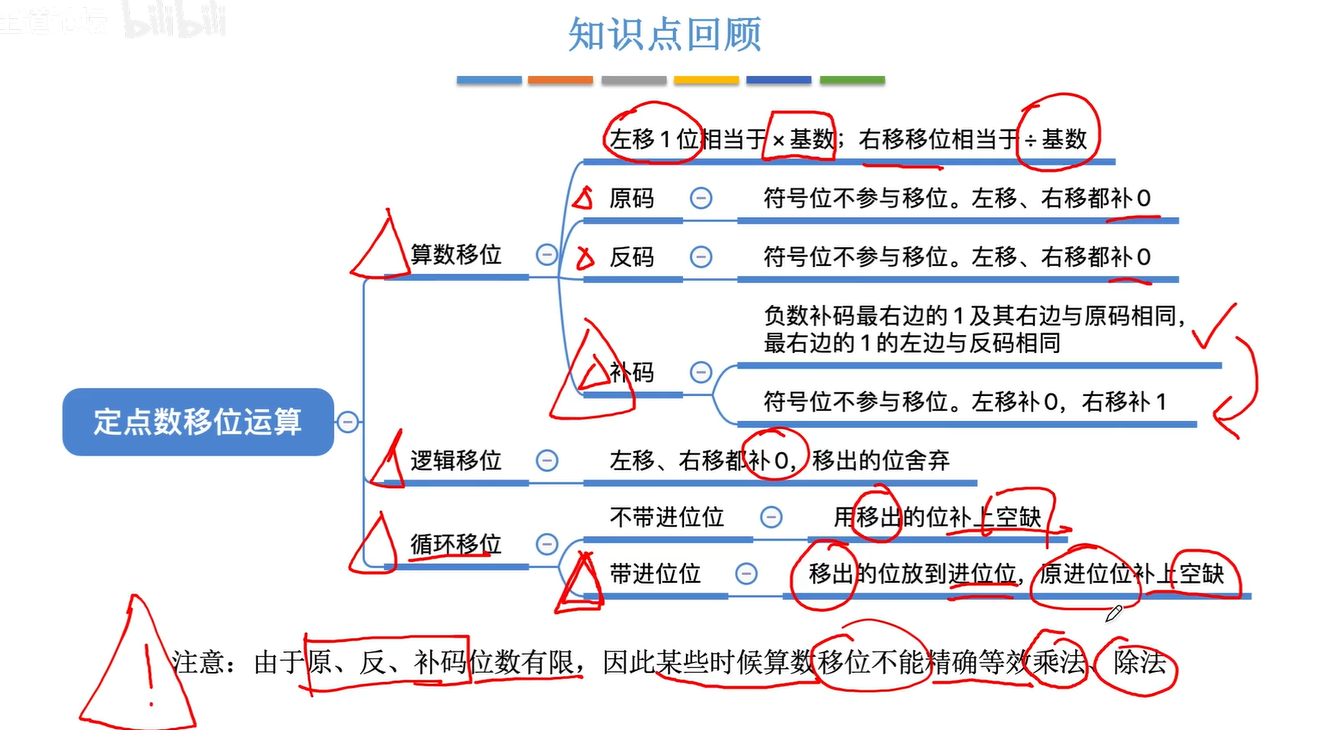
2.3移位运算
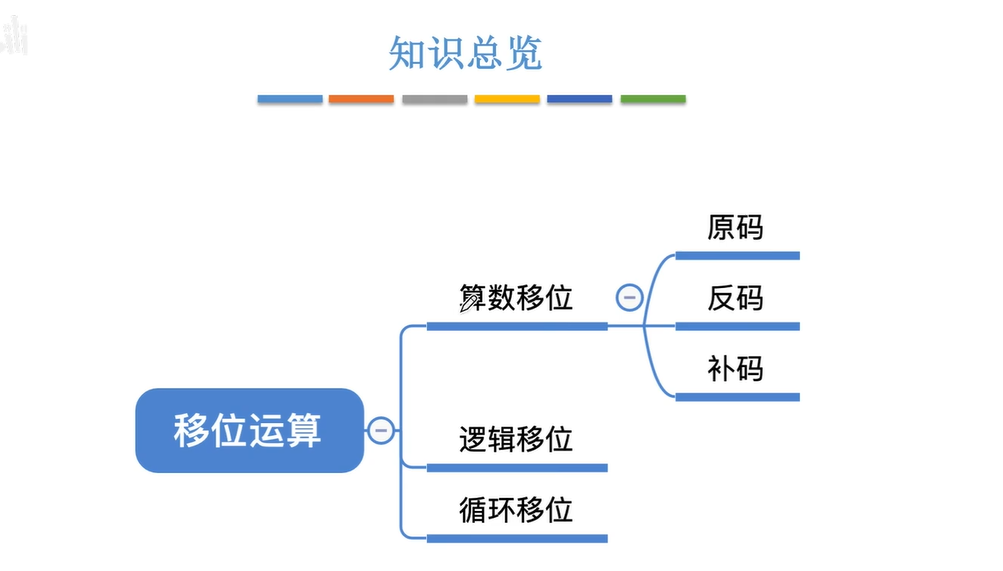
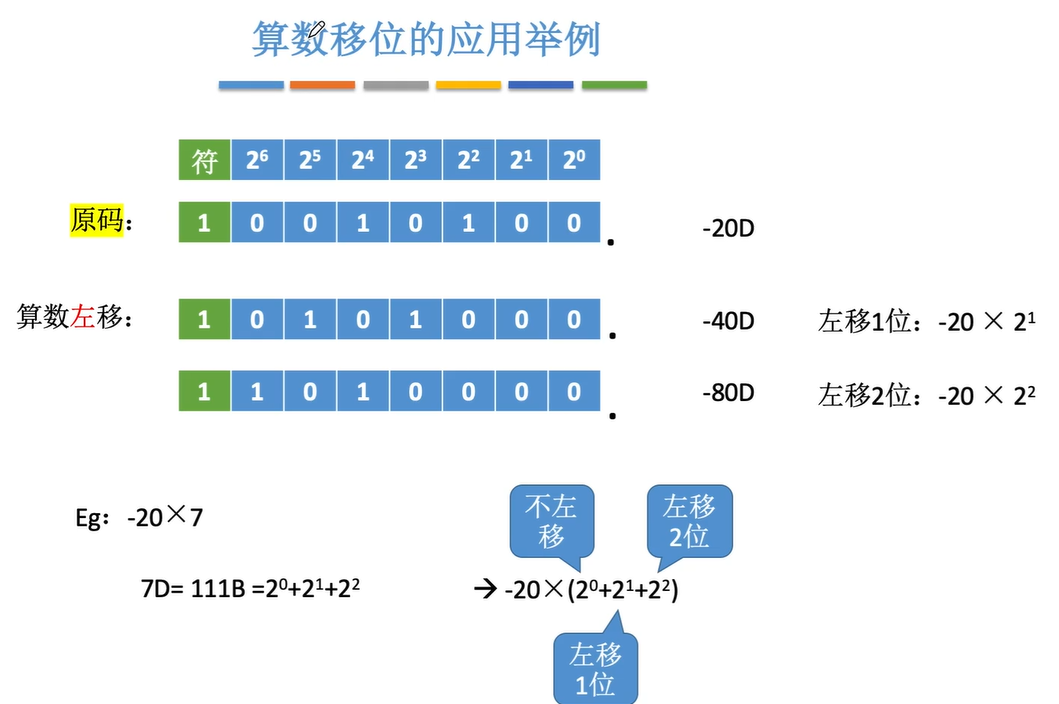
2.3.1算术移位
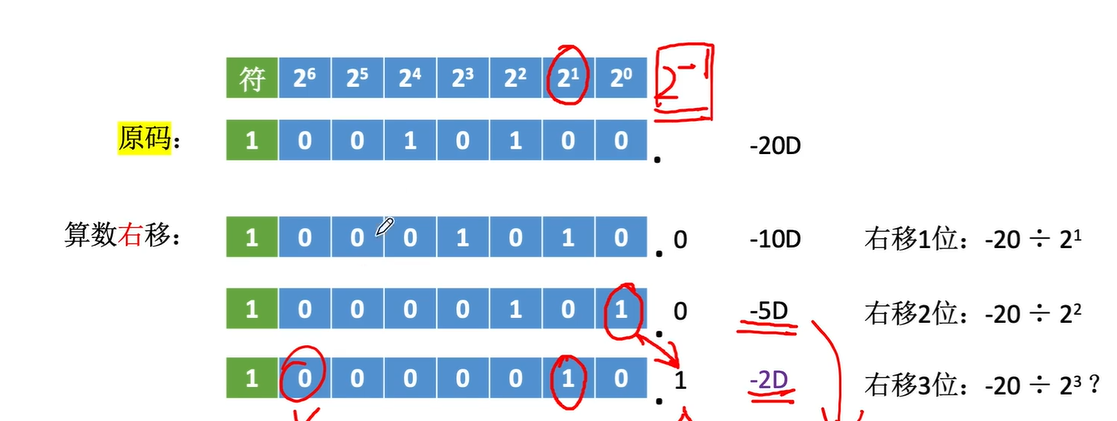
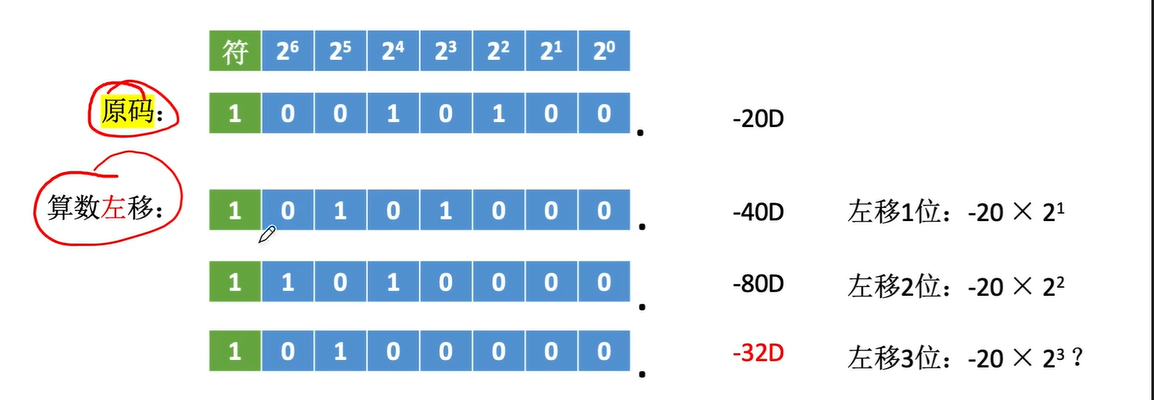
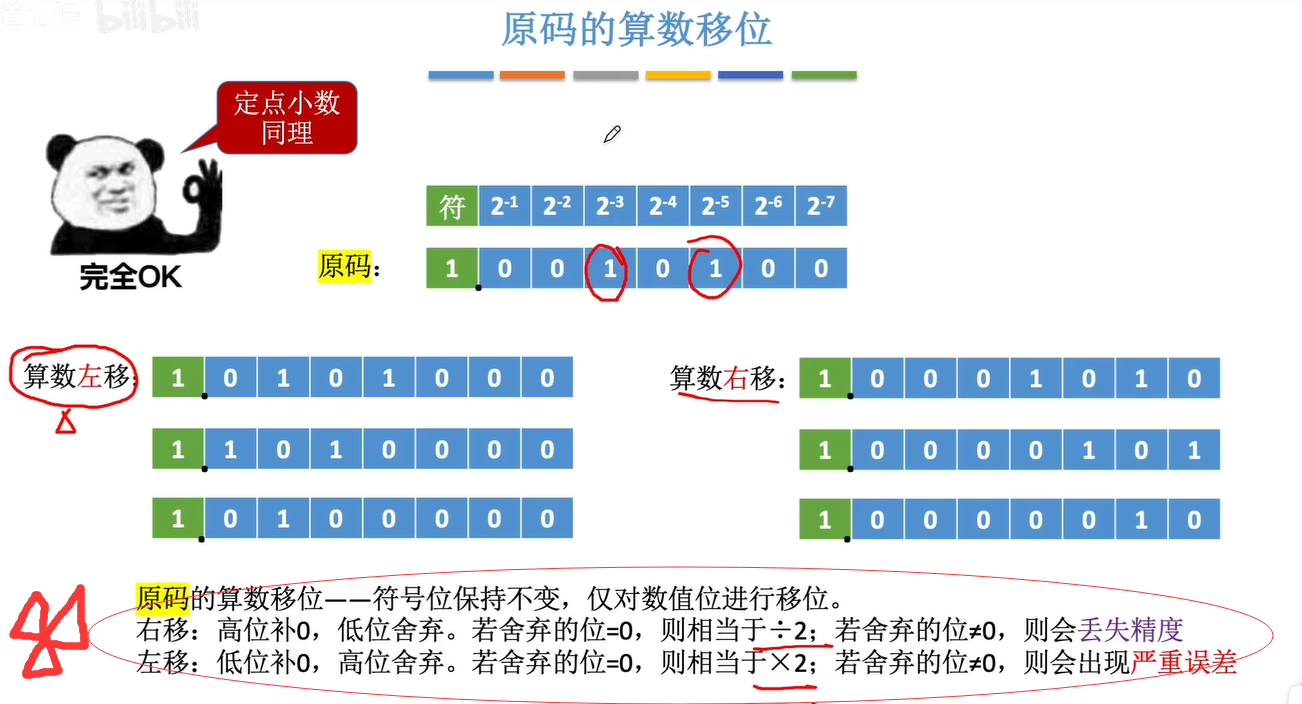
原码算术移位
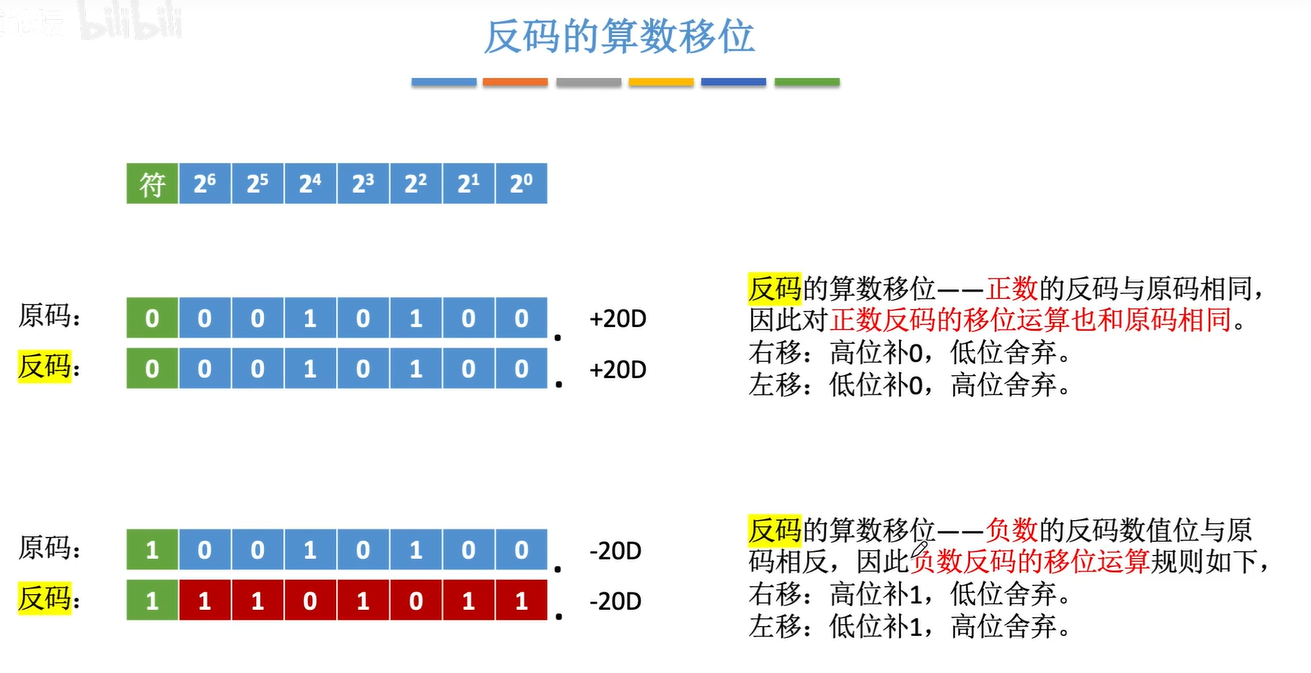
反码的算术移位
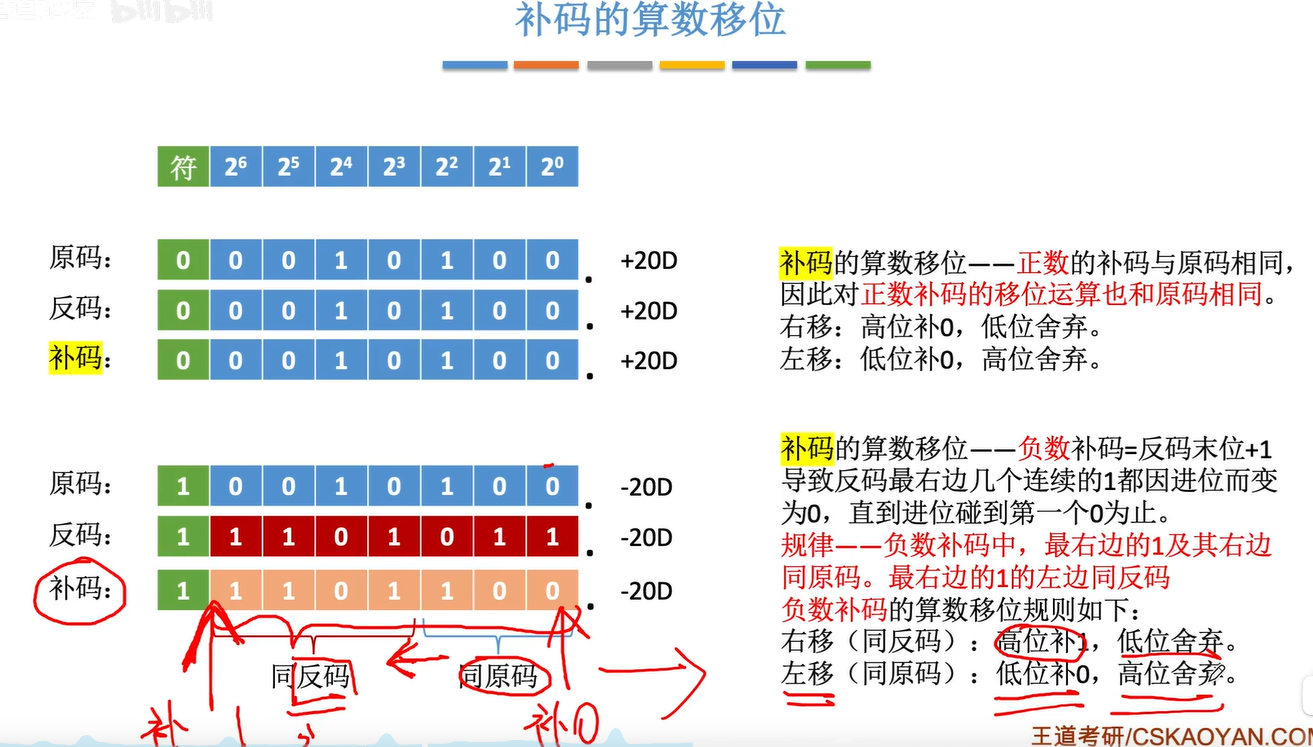
补码的算术移位
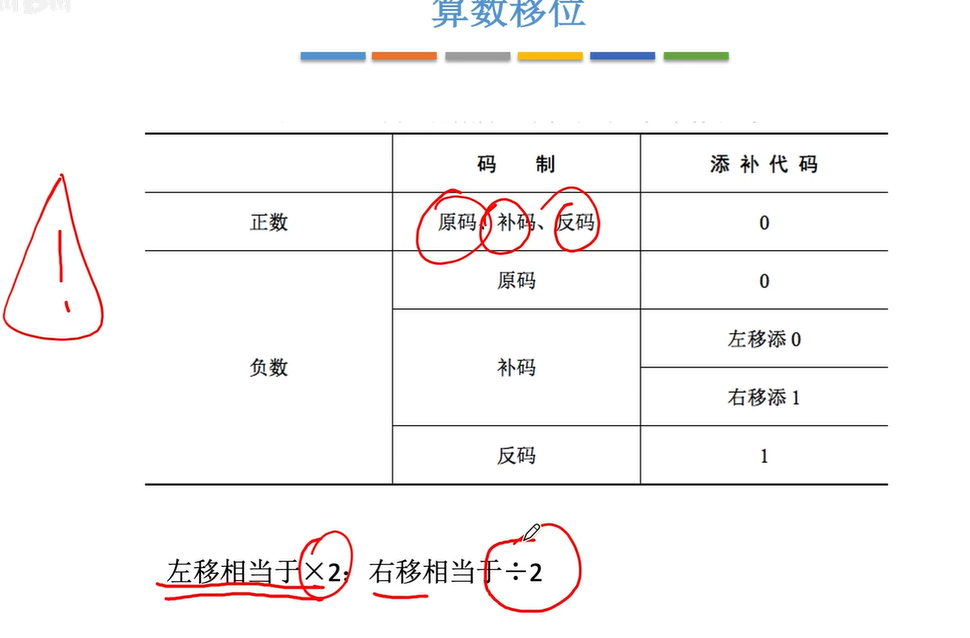
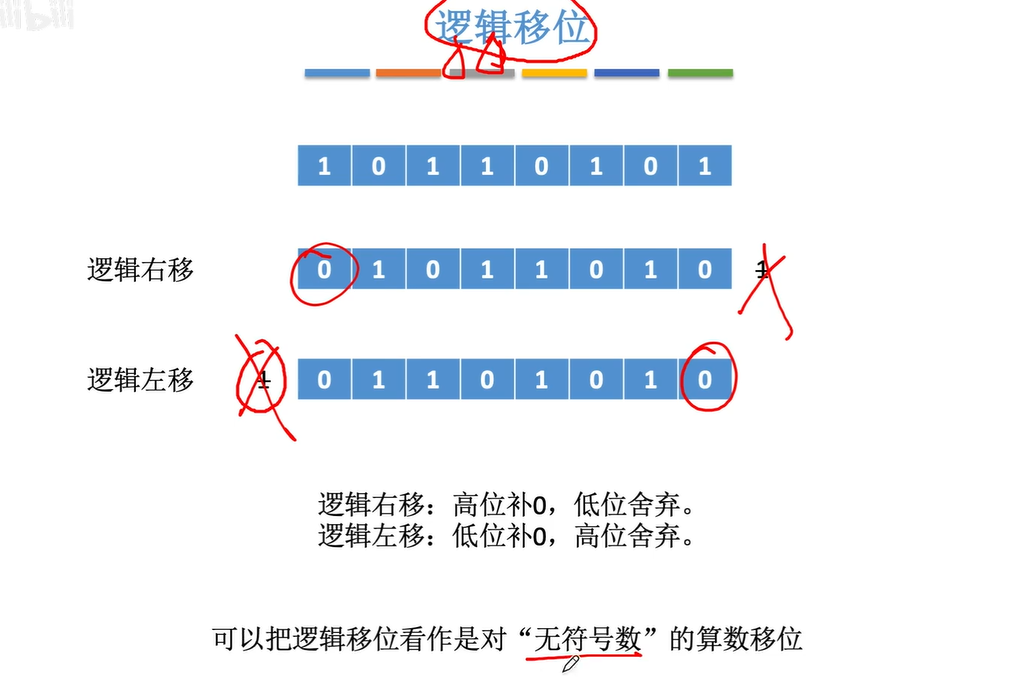
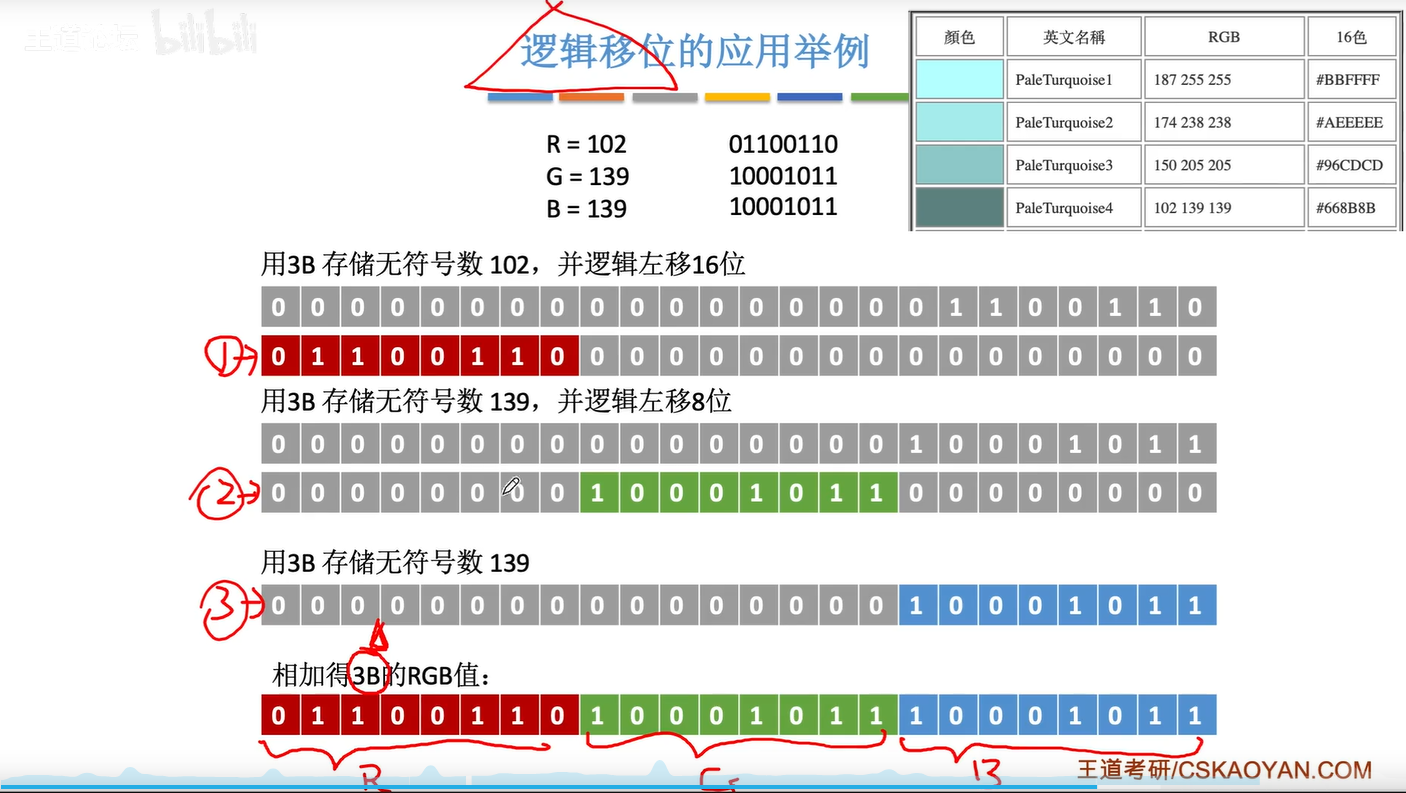
2.3.2逻辑移位
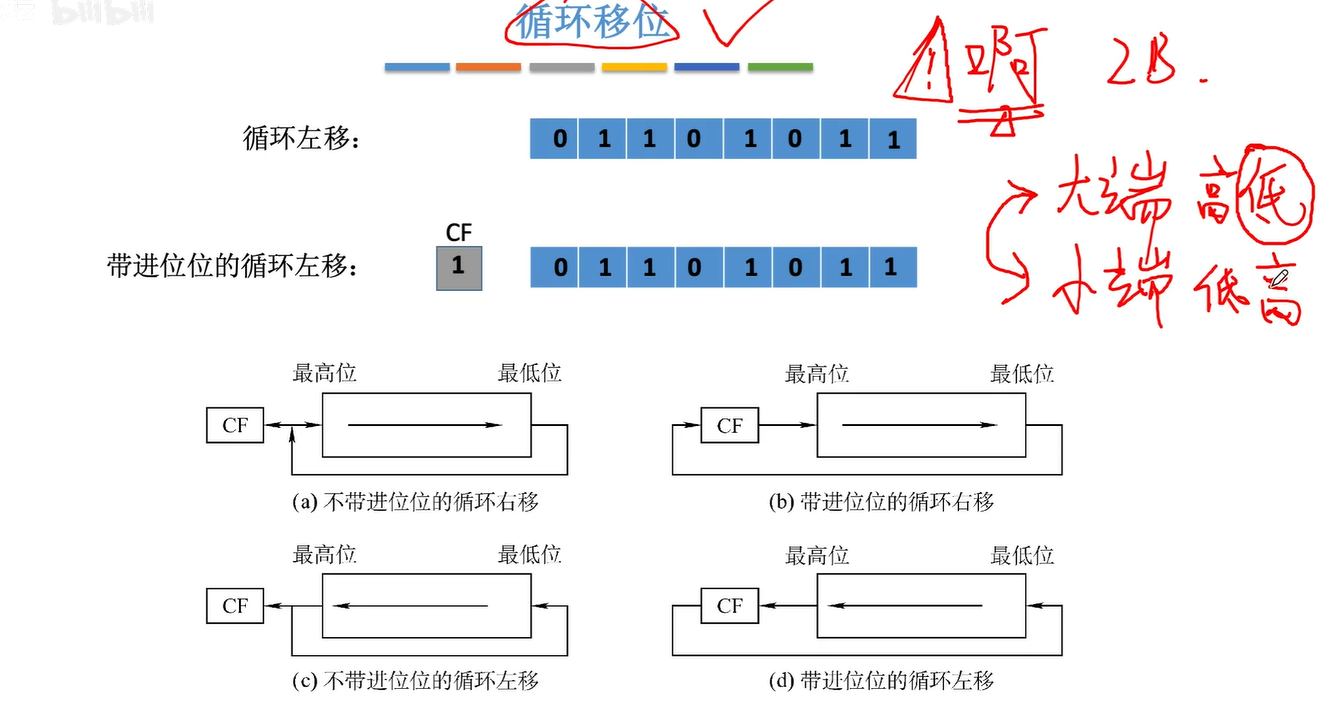
2.3.3循环移位
小结
2.4加减运算
2.4.1原码的加减法
2.4.2补码的加减法运算
2.4.3 溢出判断
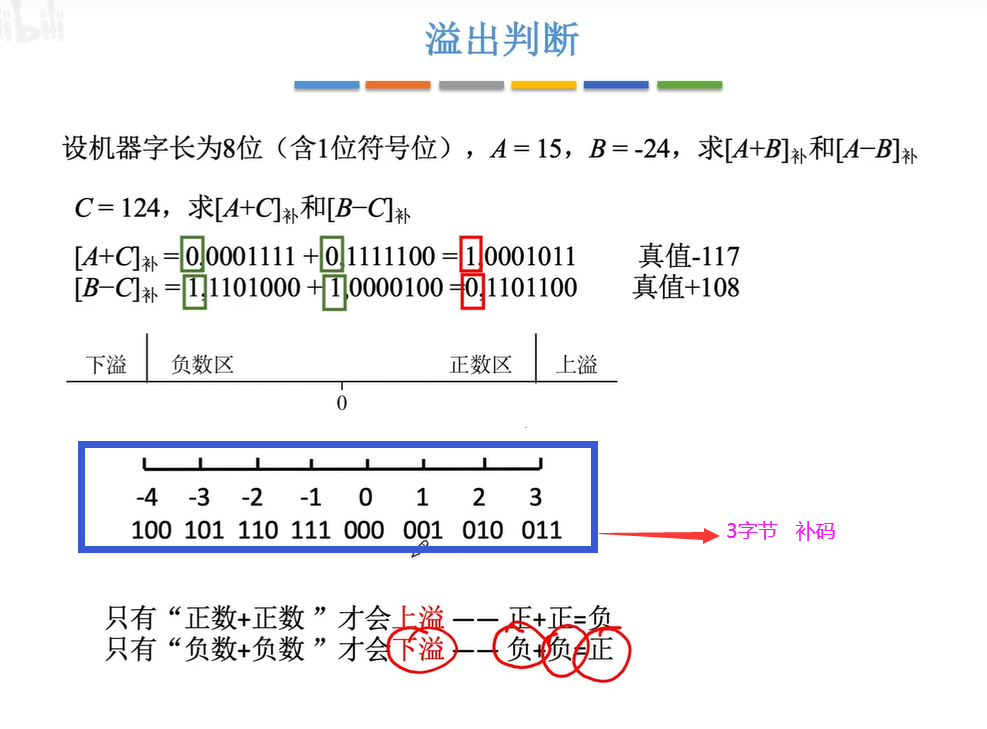
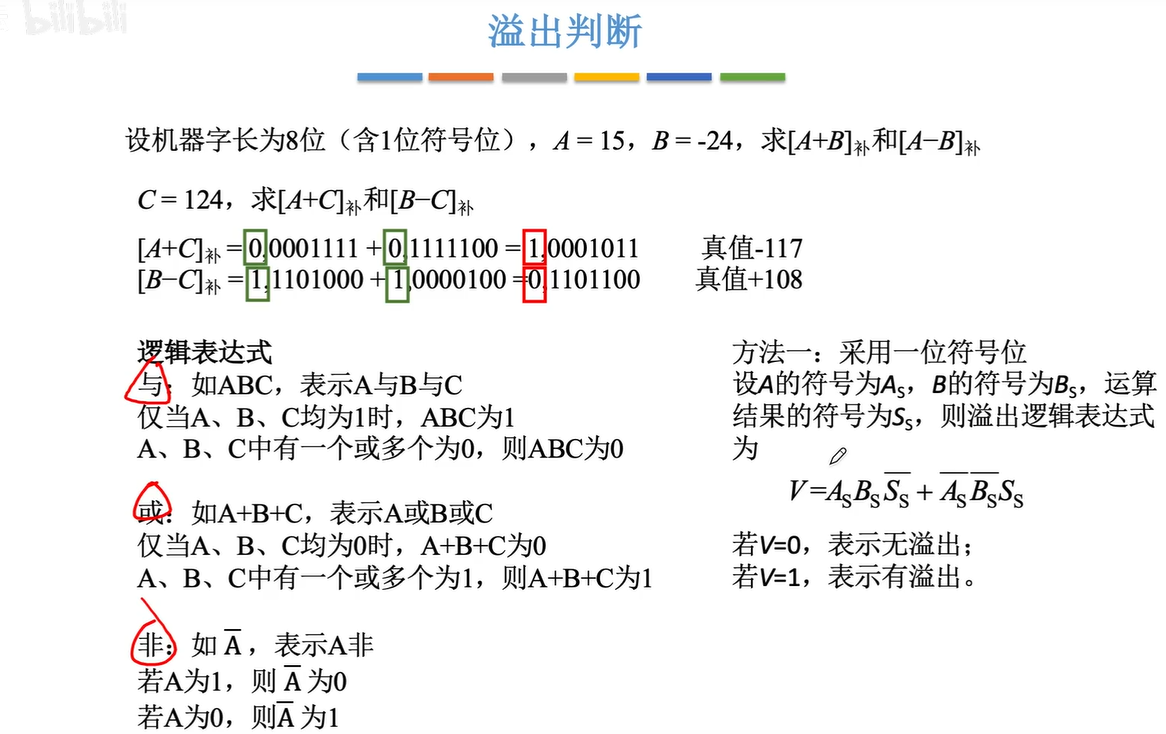

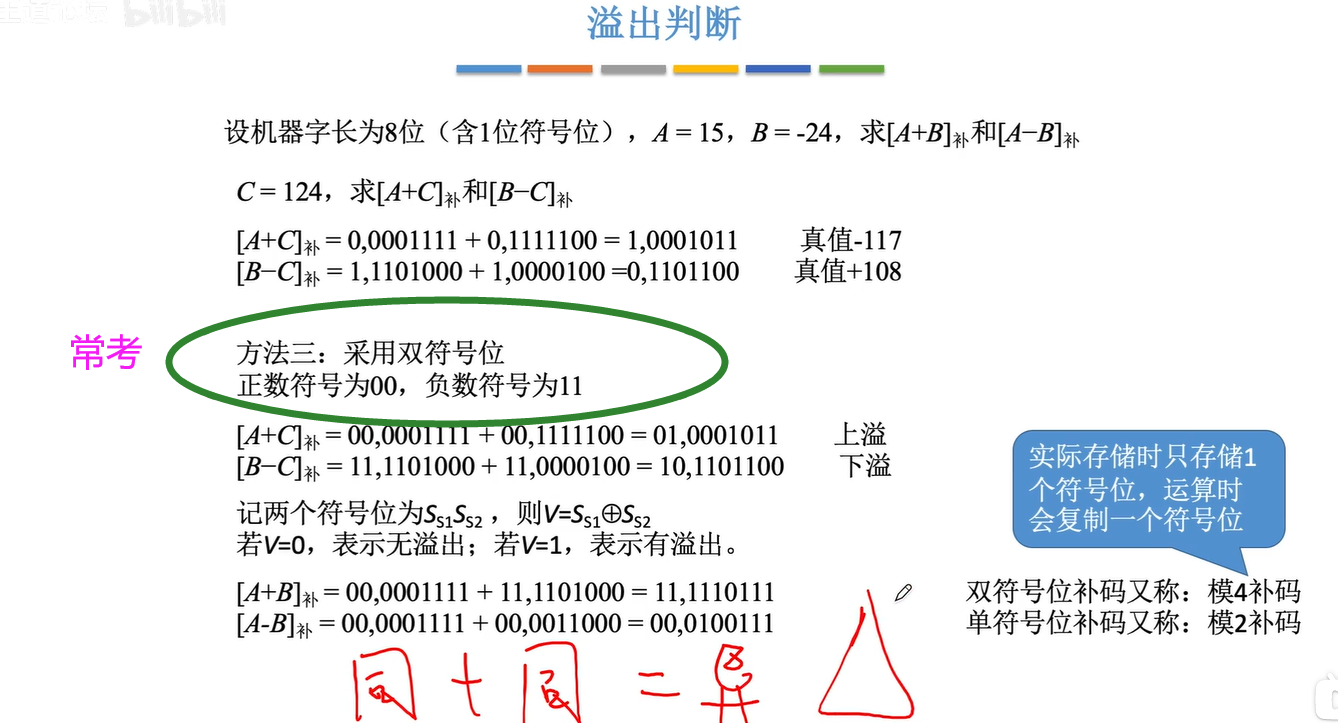
2.4.4符号扩展

小结
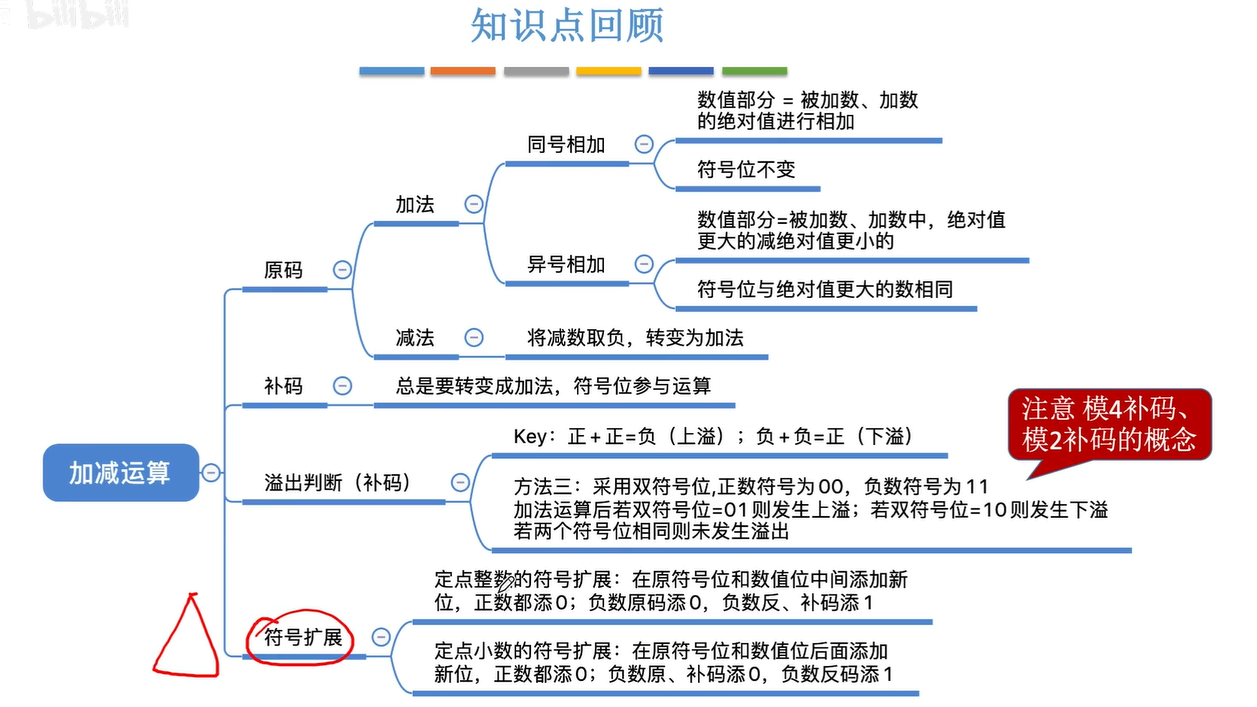
2.5乘法运算
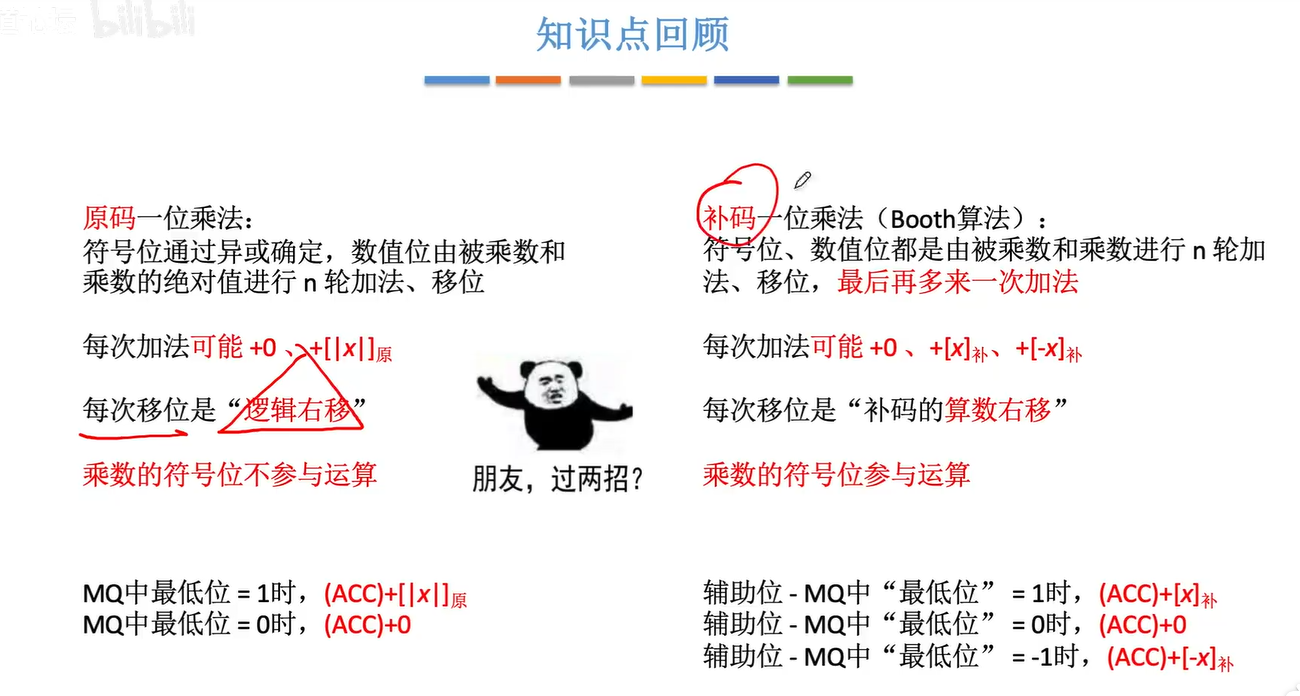
2.5.1 原码的一位乘法


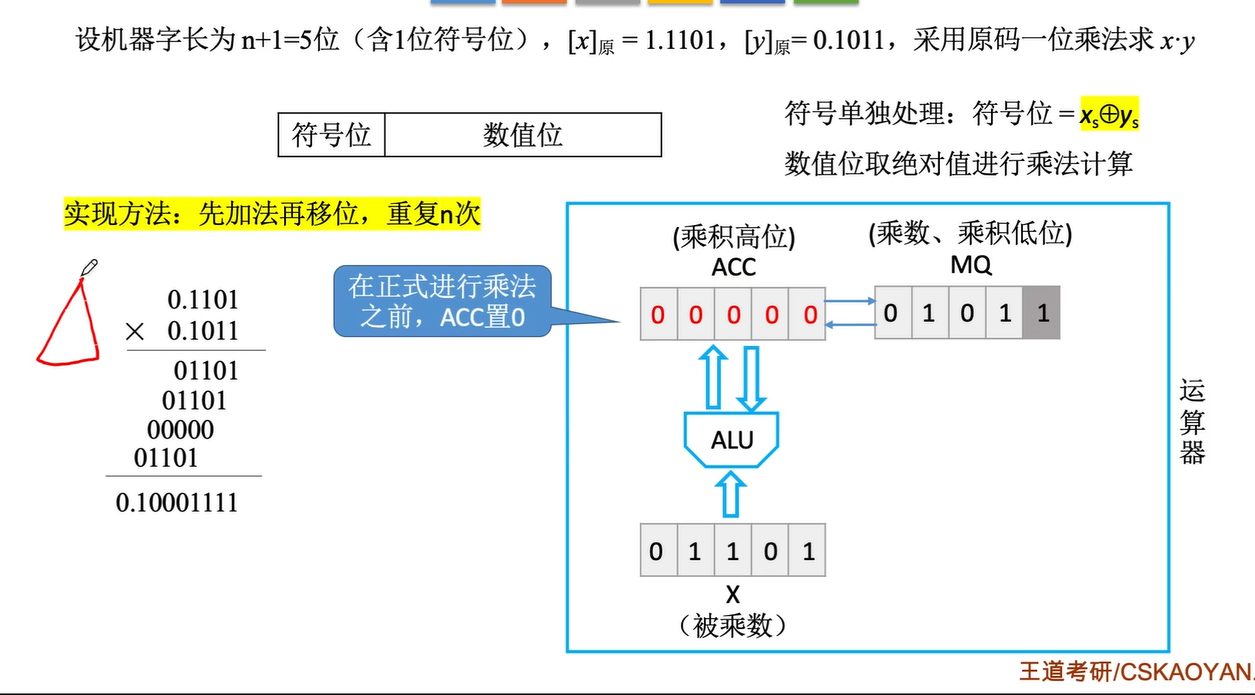
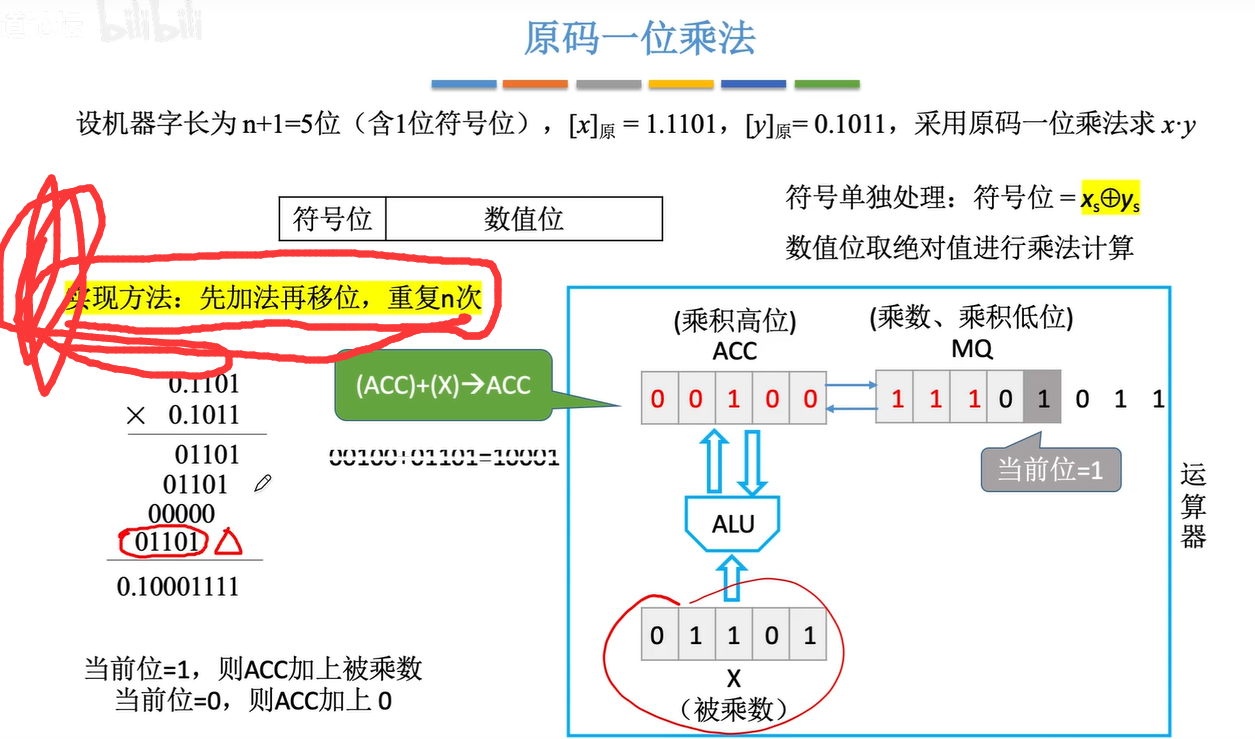
ACC 中存放部分结果
MQ 中存放 乘数
X 中存放被乘数
每运算一次 就进行一次ACCMQ中右移

2.5.2 补码的一位乘法
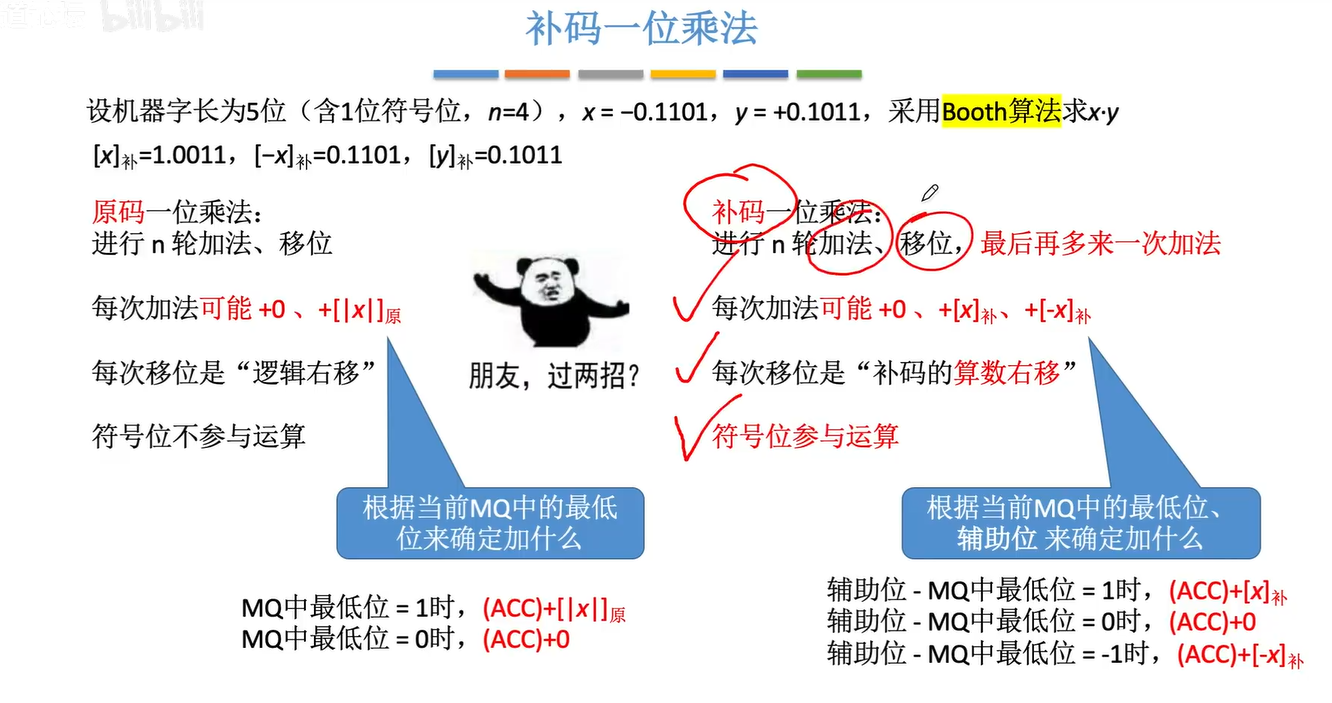
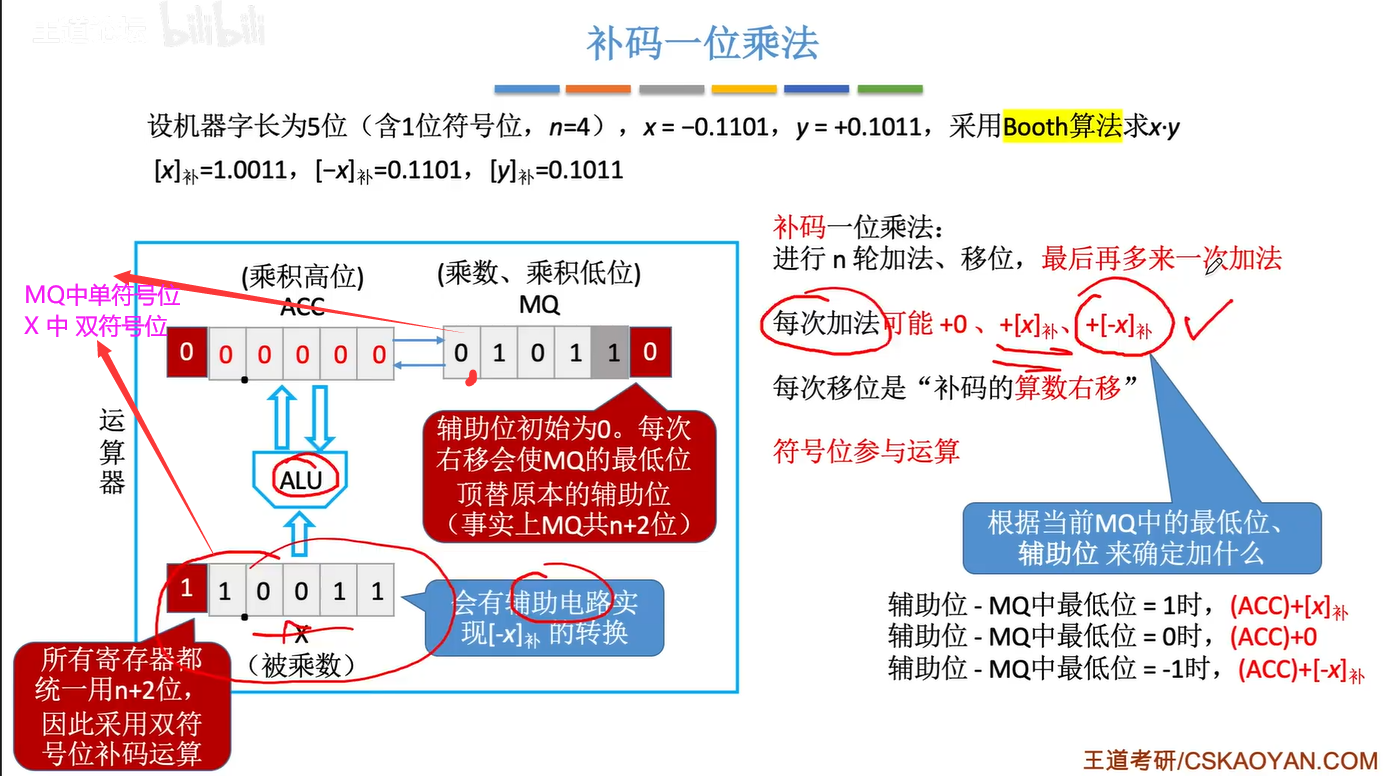
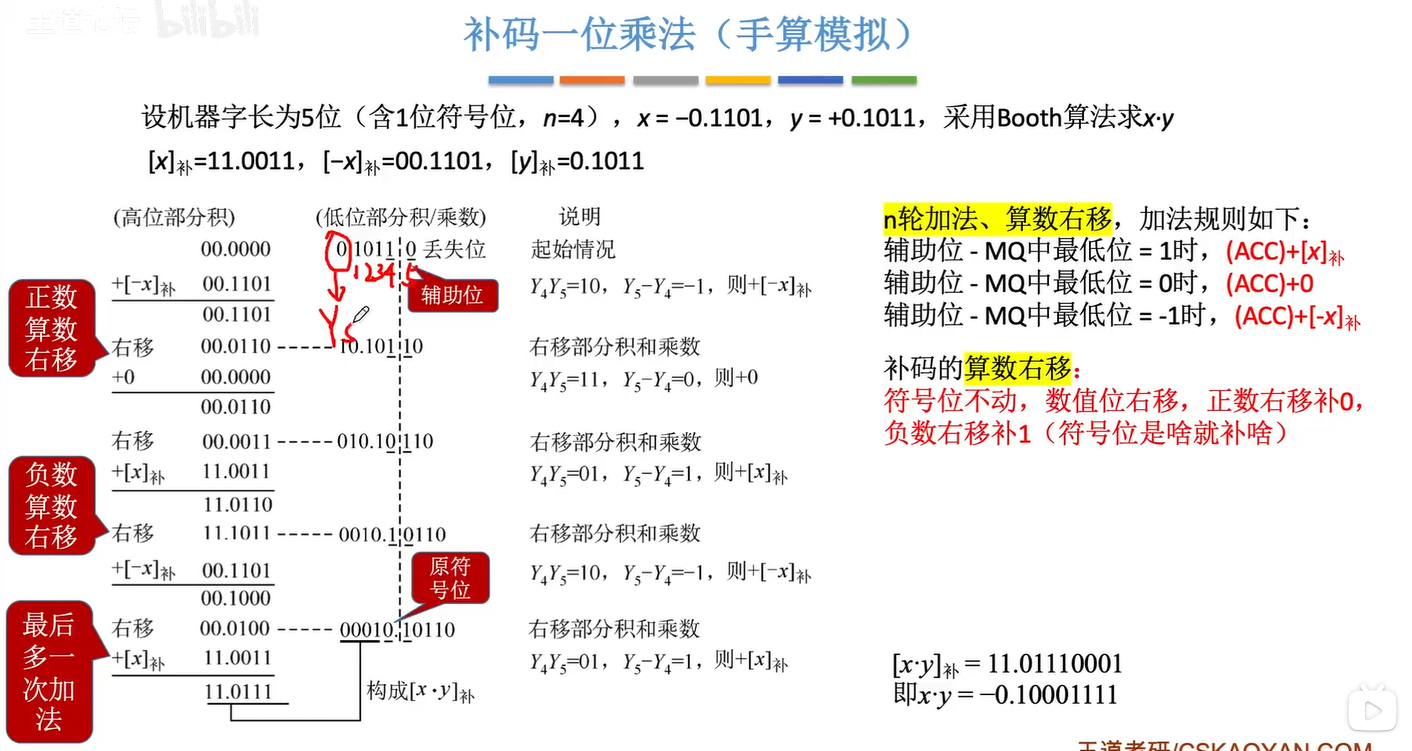
对比
2.6 除法运算
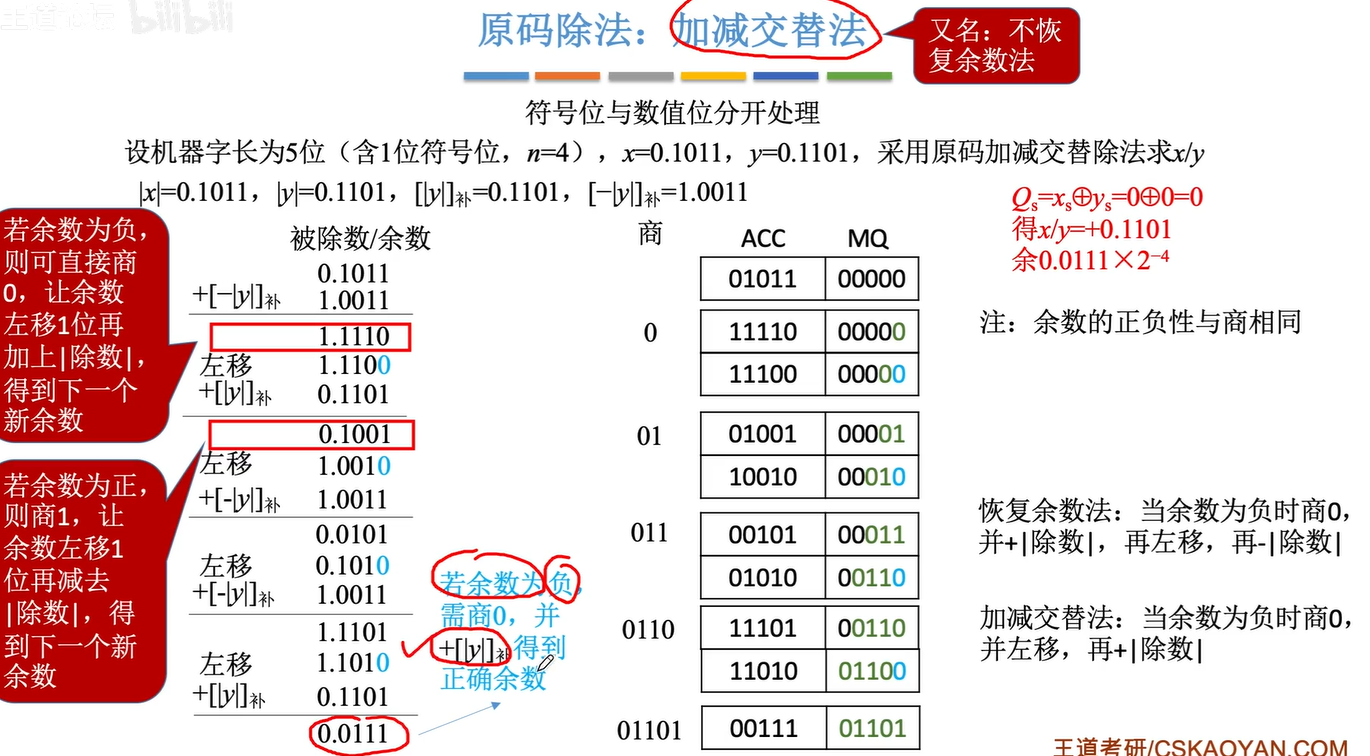
2.6.1原码的除法运算
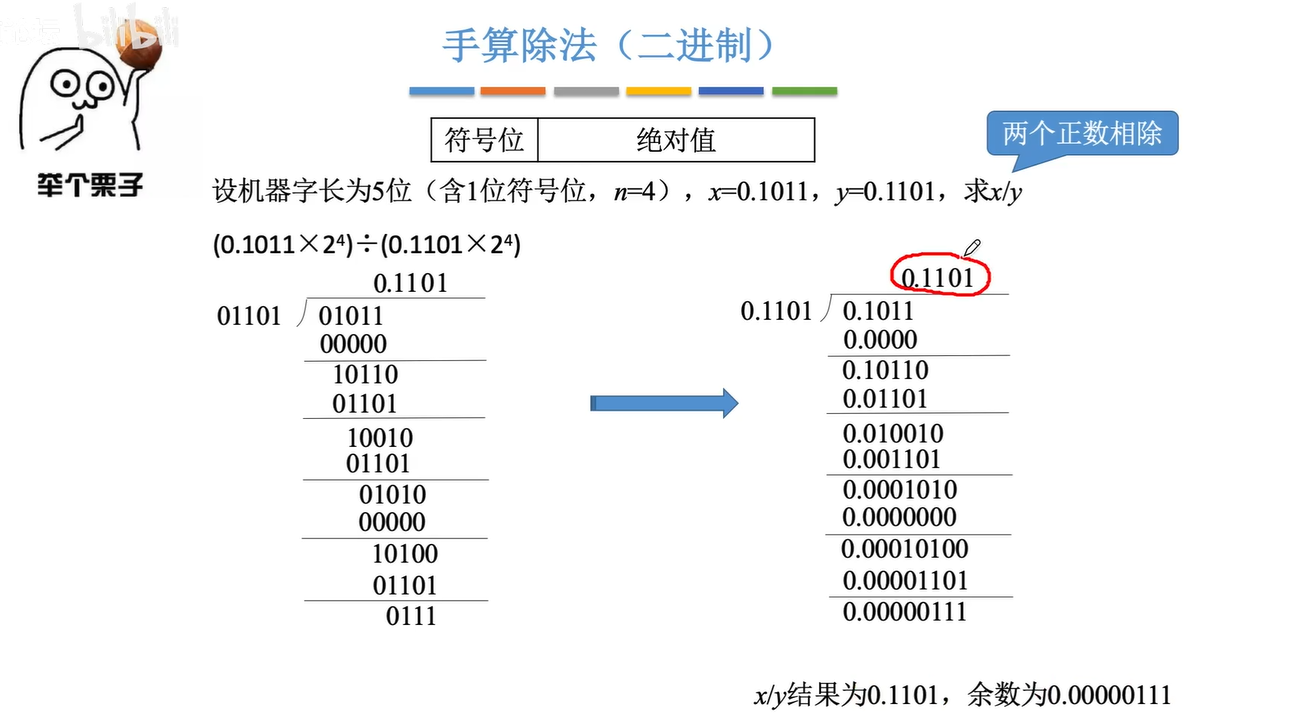
规律: 忽略小数点,每确定一位商,进行一次减法,得到4位余数,在余数末尾补o,再确定下一位商。确定5位商即可停止(机器字长为5位)
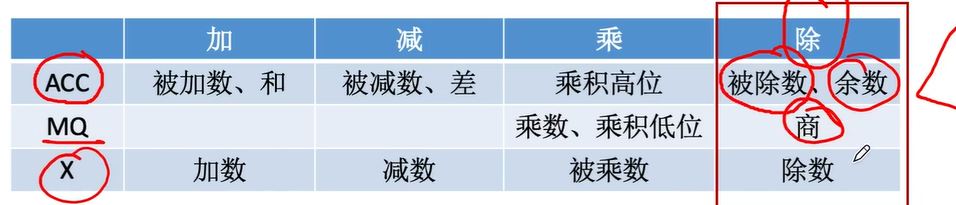
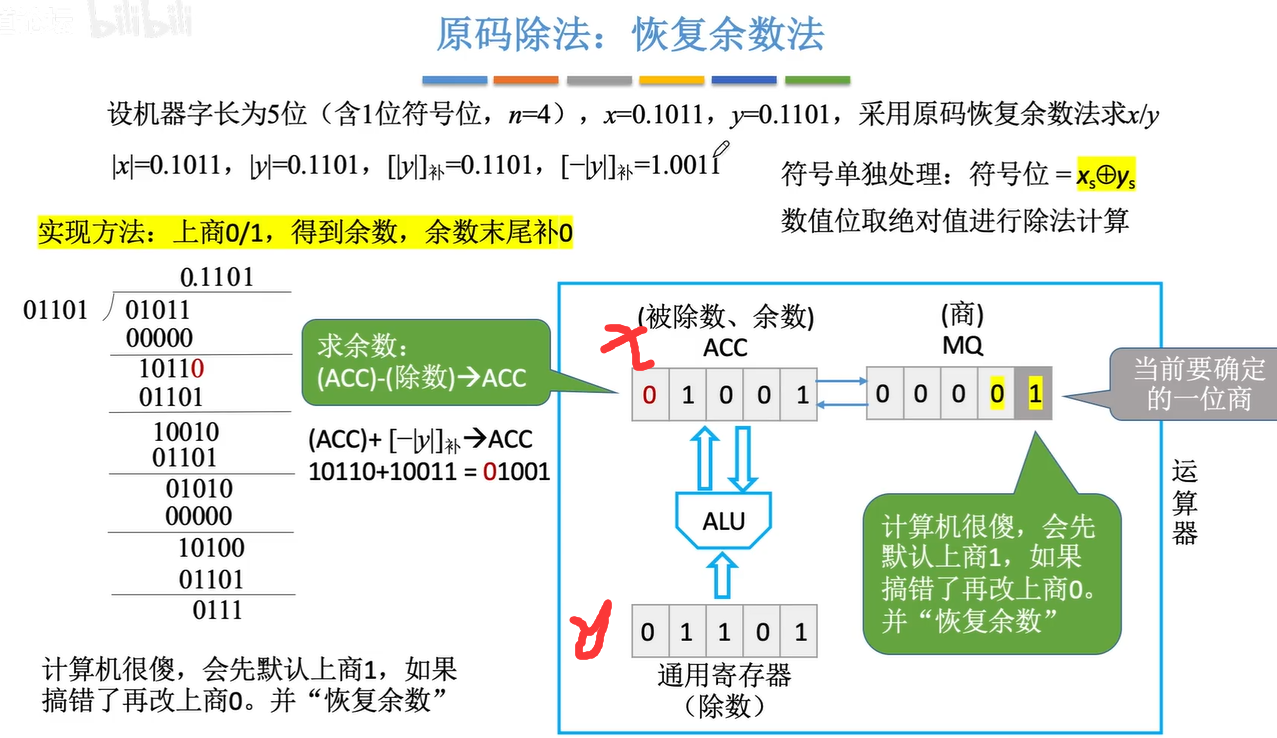
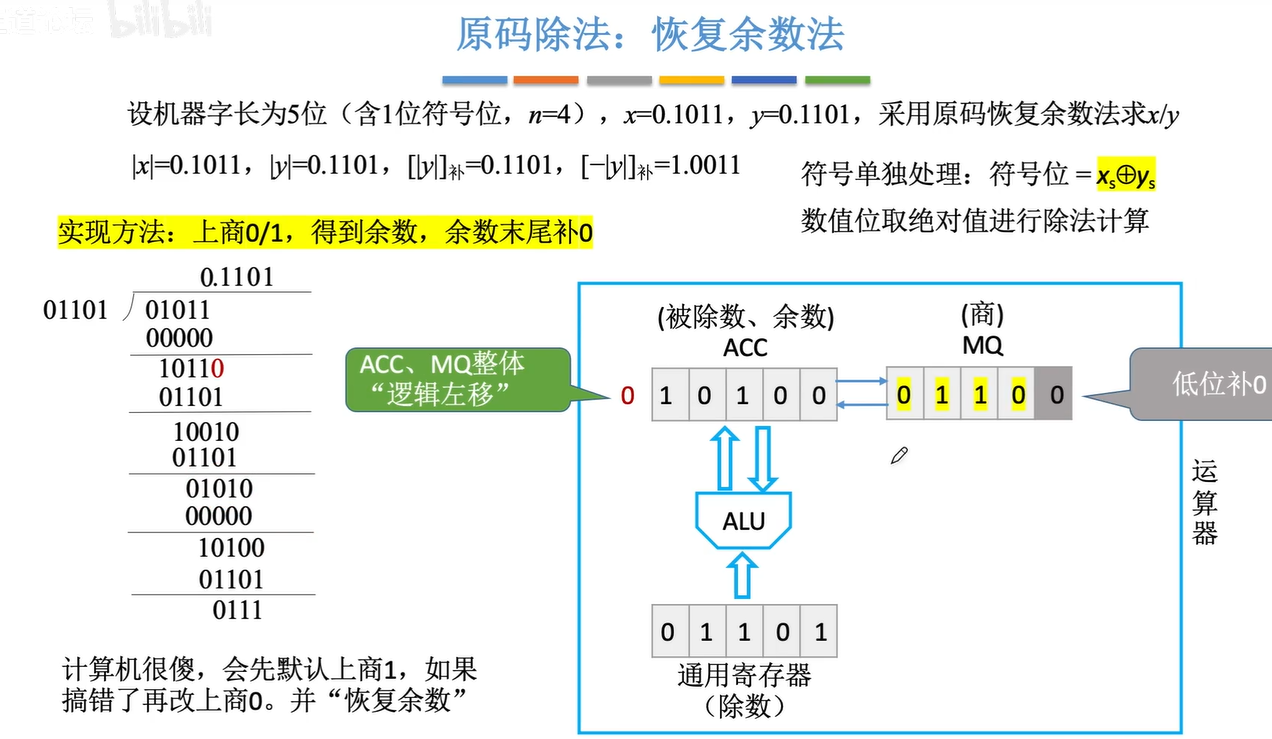
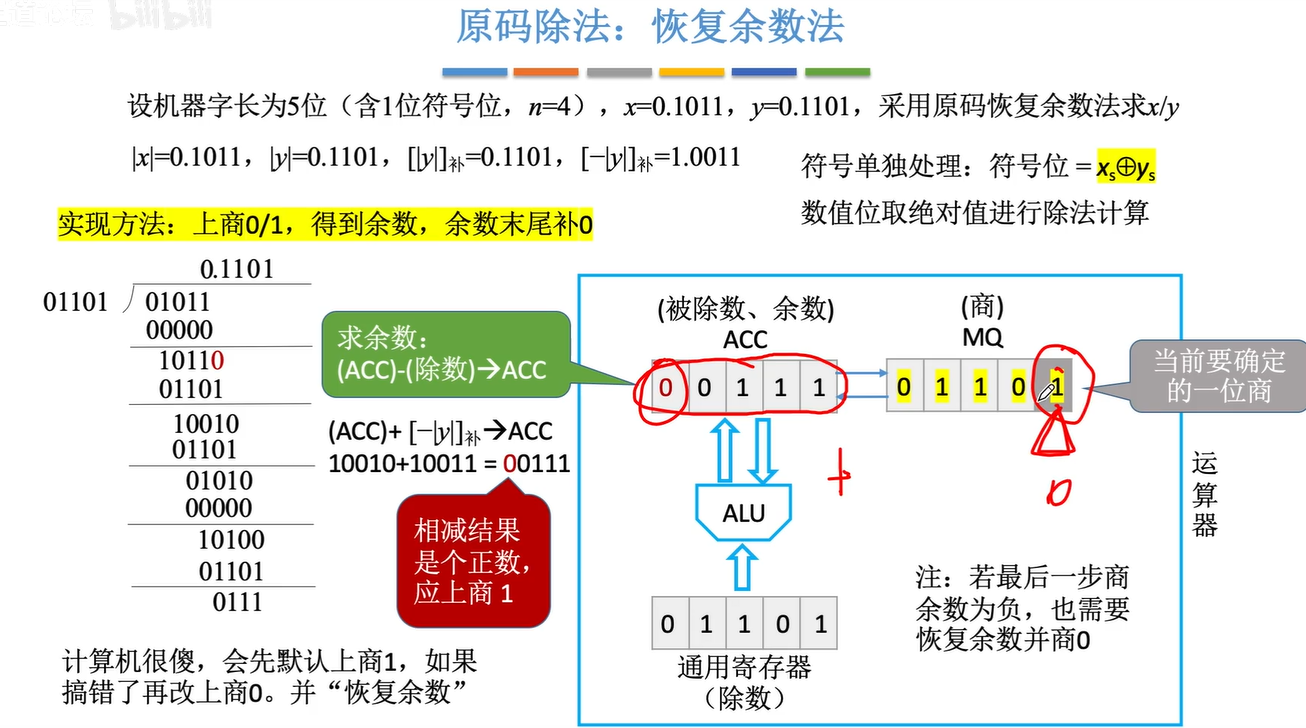
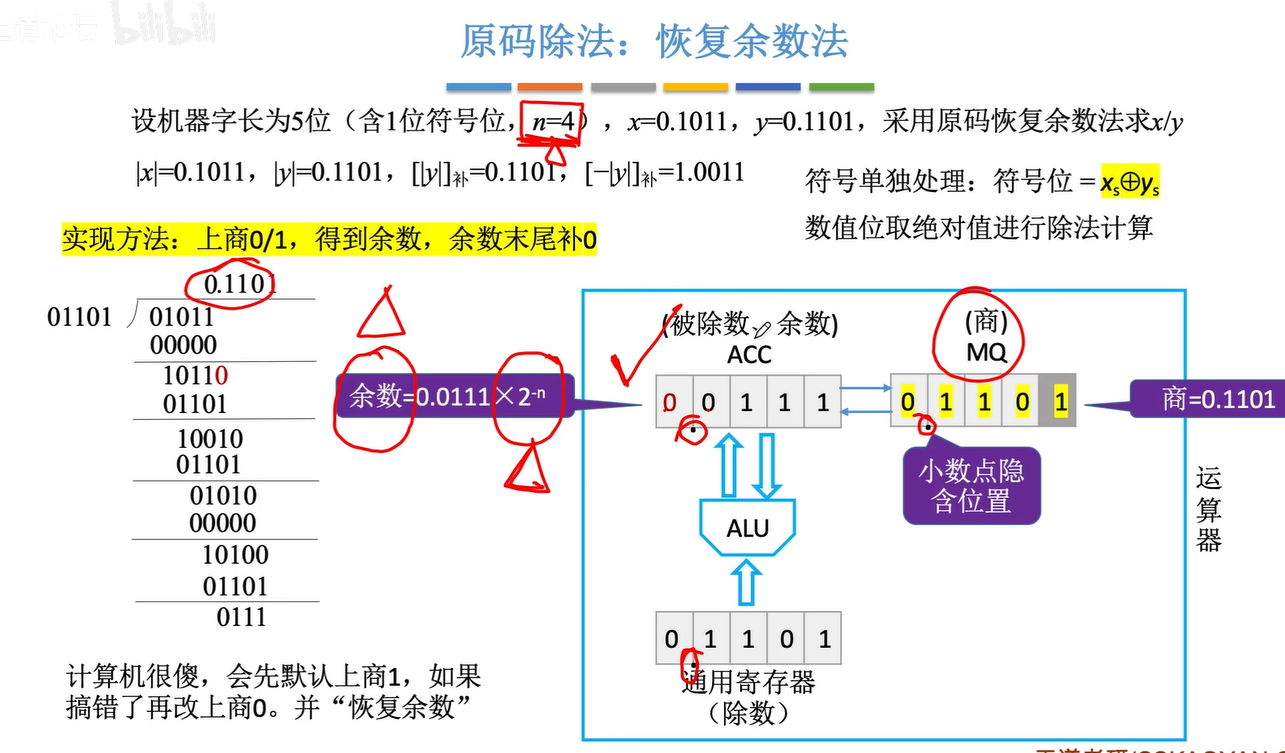
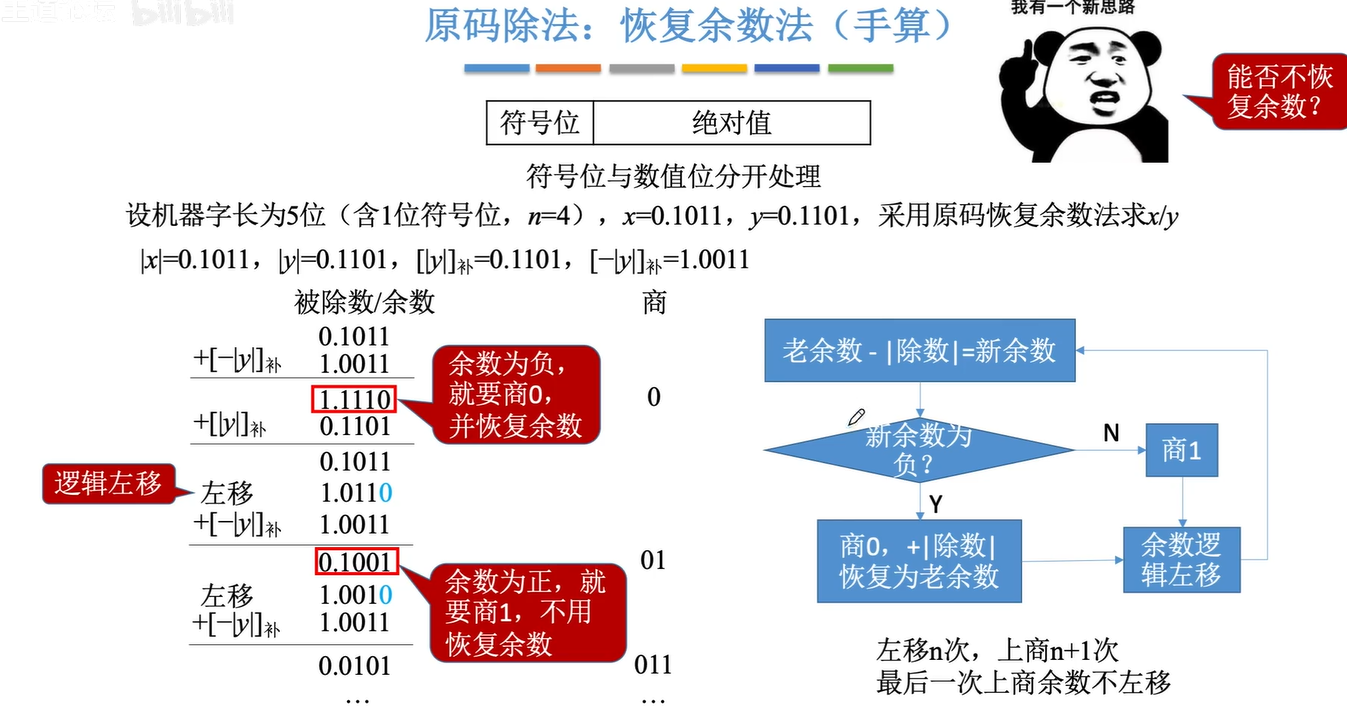
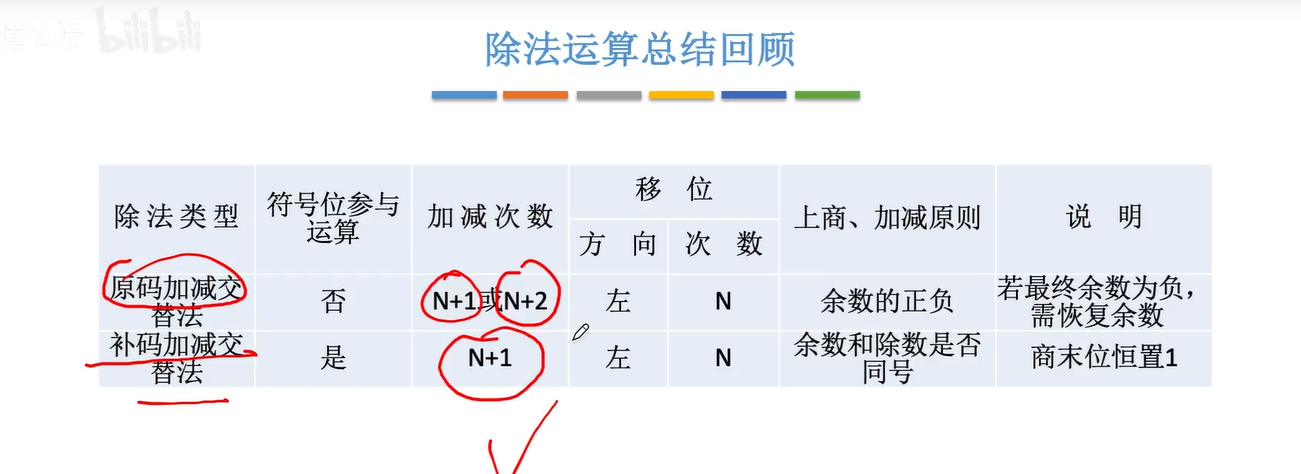
加减交替法
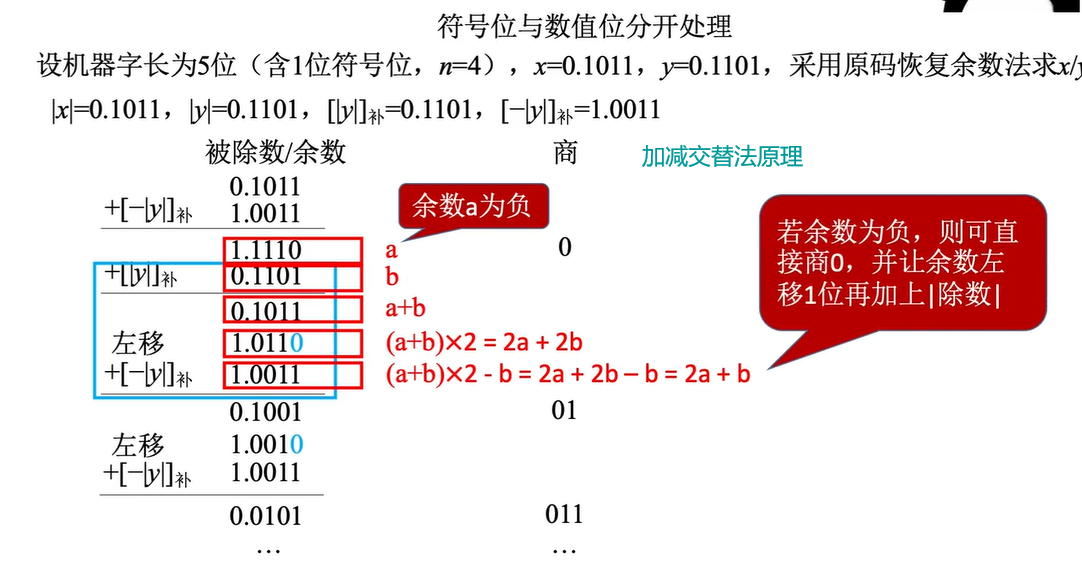
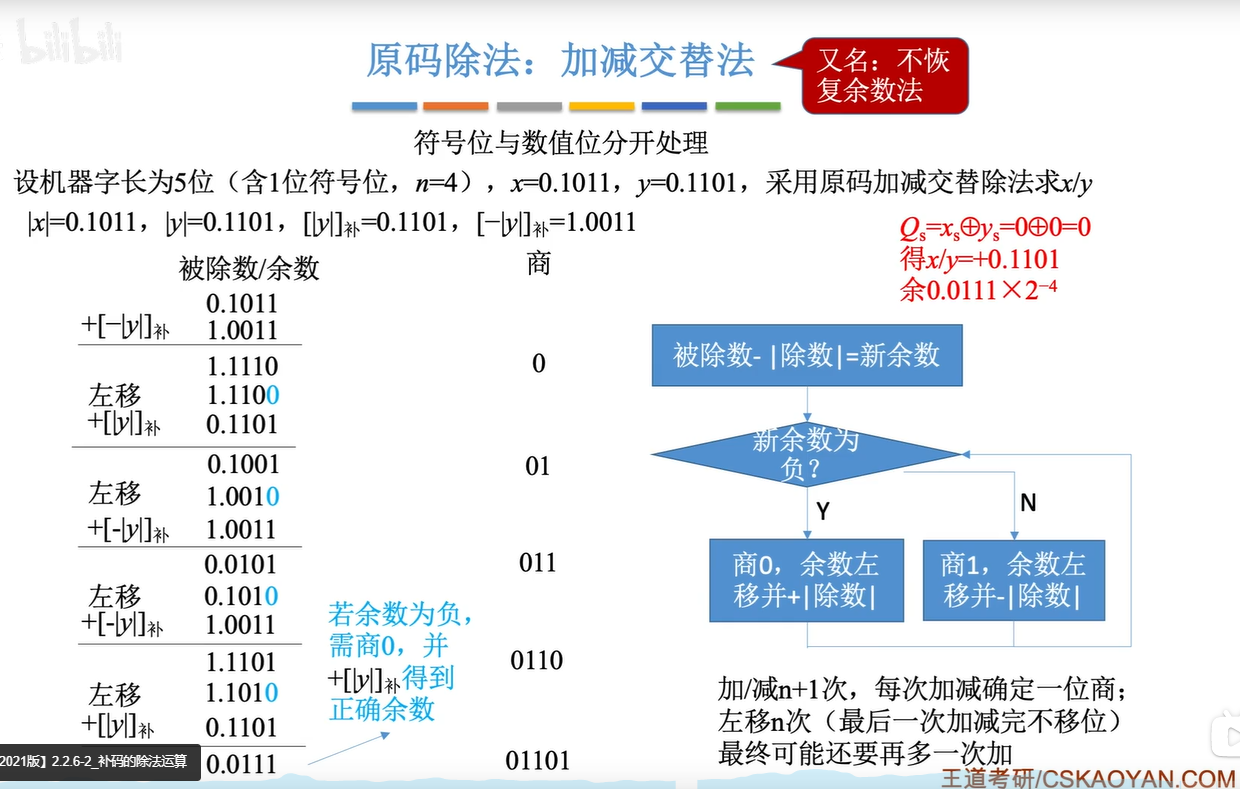
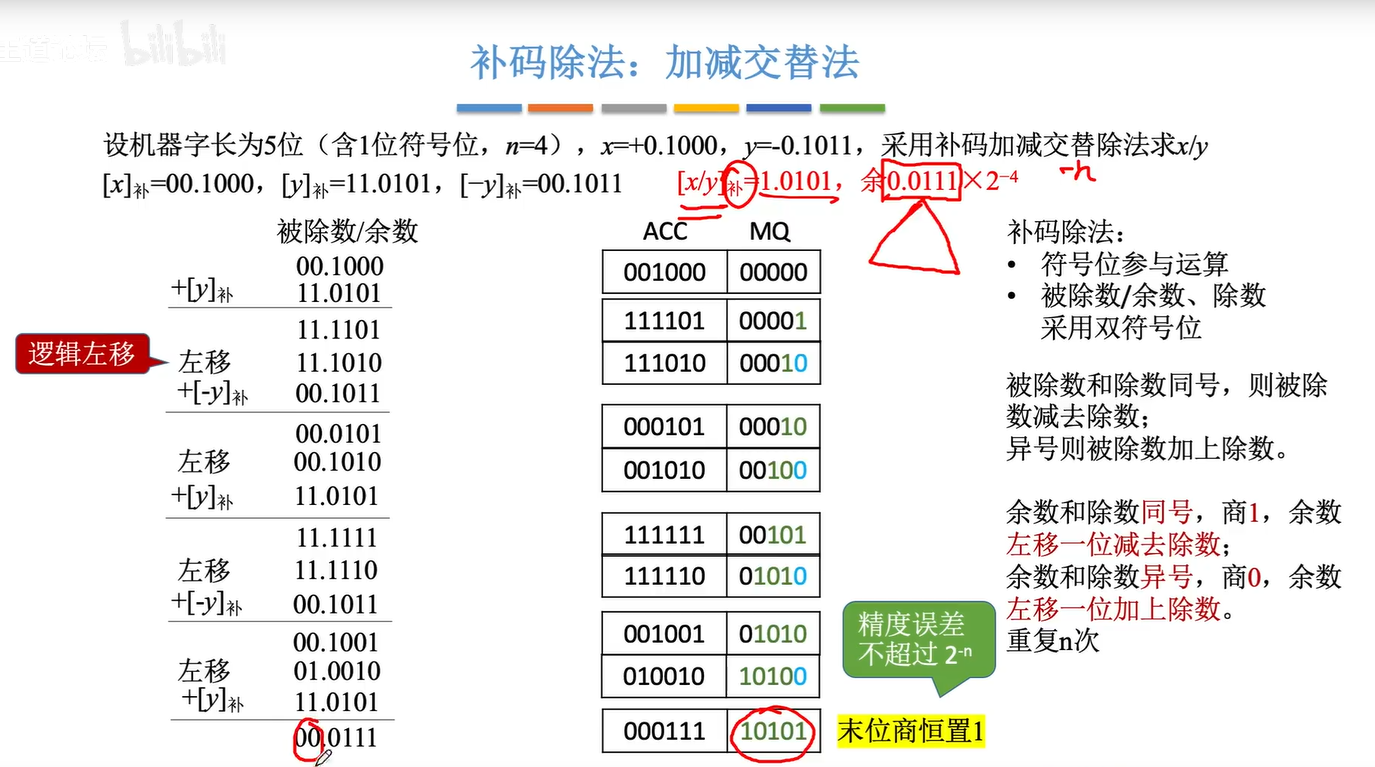
2.6.2补码的除法运算
2.7强制类型转换

2.8数据的存储和排列
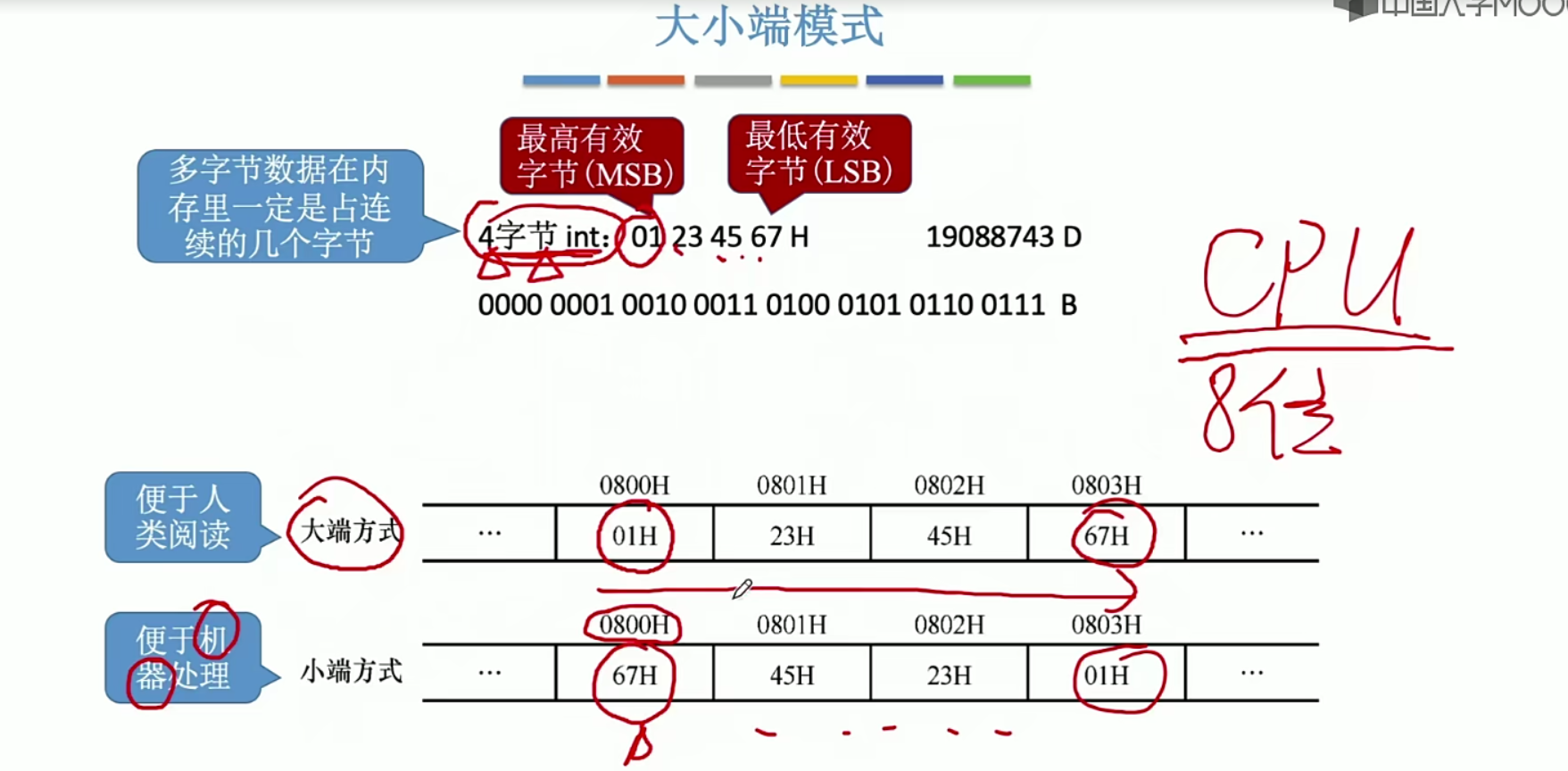
按字
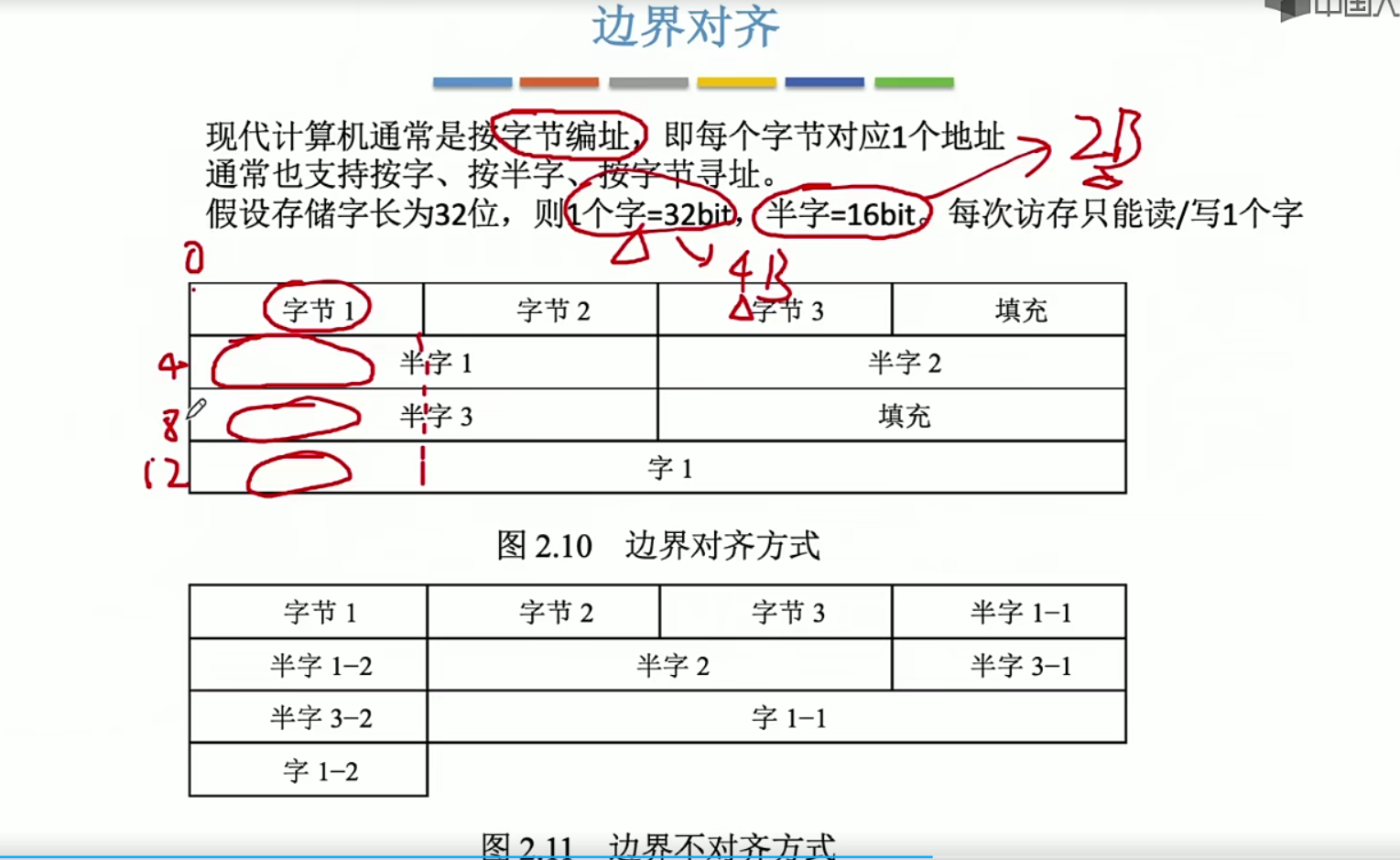
字地址转换成字节地址 左移两位 例 2号字 10 左移两位 1000 即地址为8
半字地址转换成字节地址 左移一位 2 10 100 4
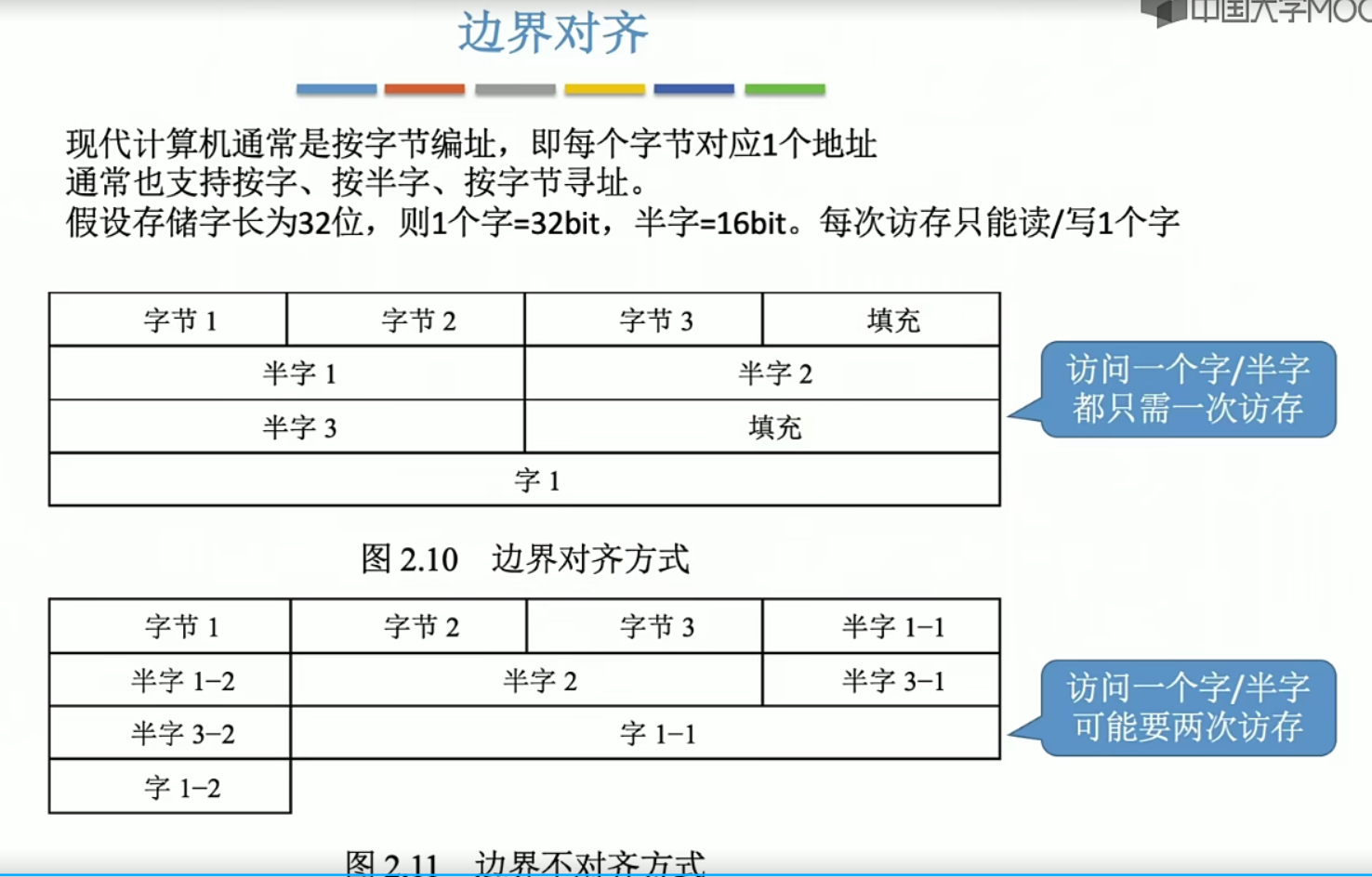
2.9浮点数的表示
2.9.1浮点数的表示
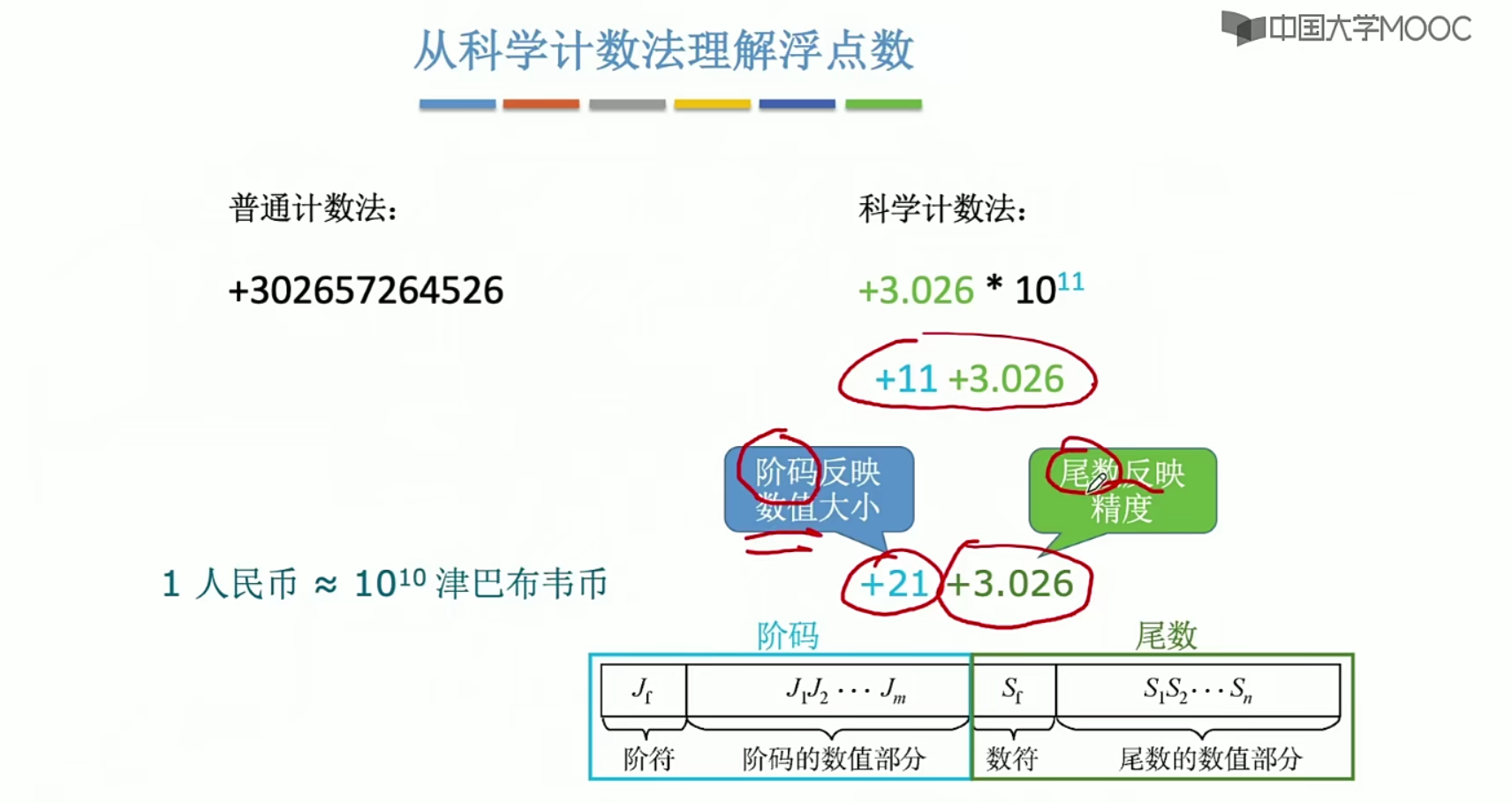

练习


2.9.2浮点数尾数的规格化
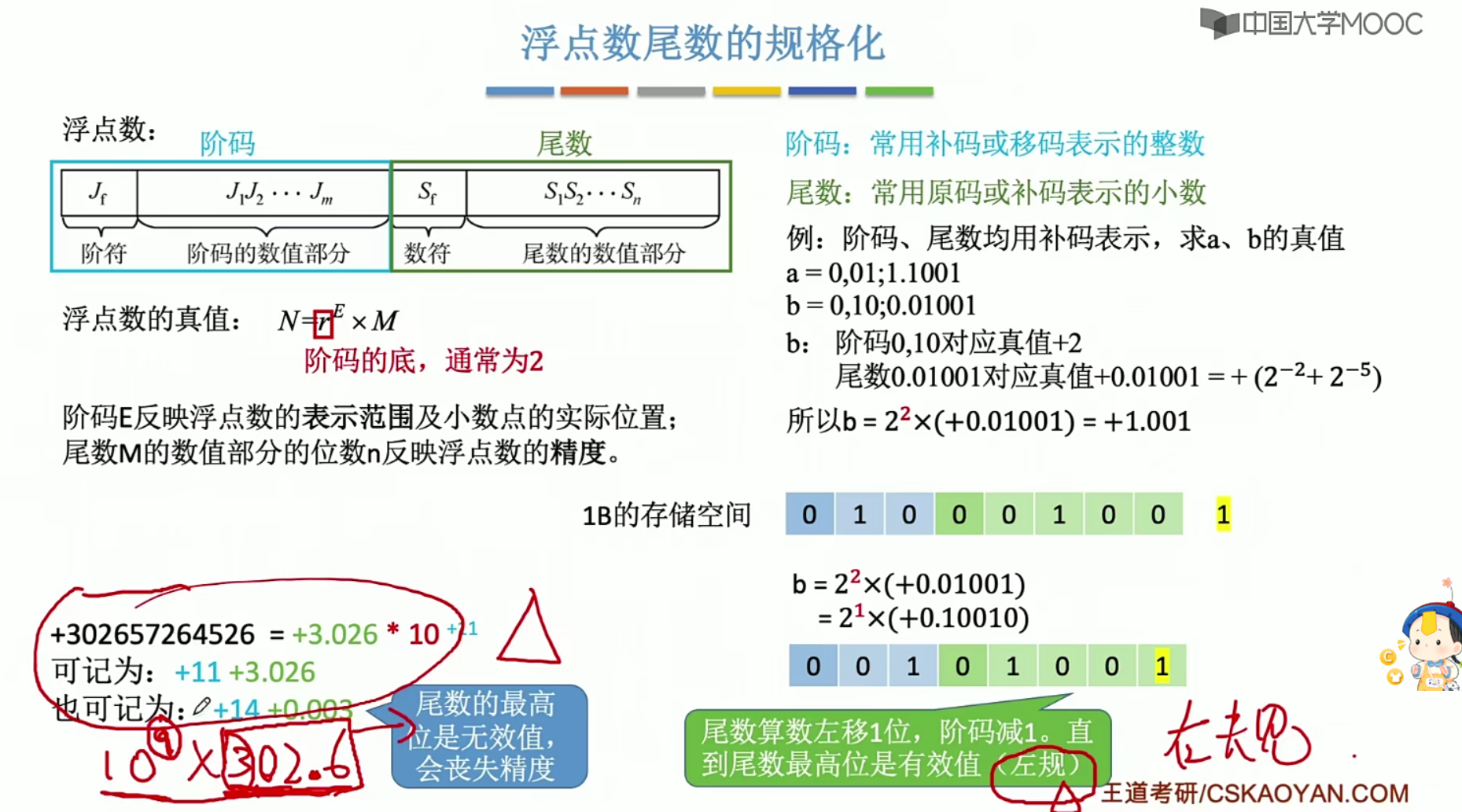

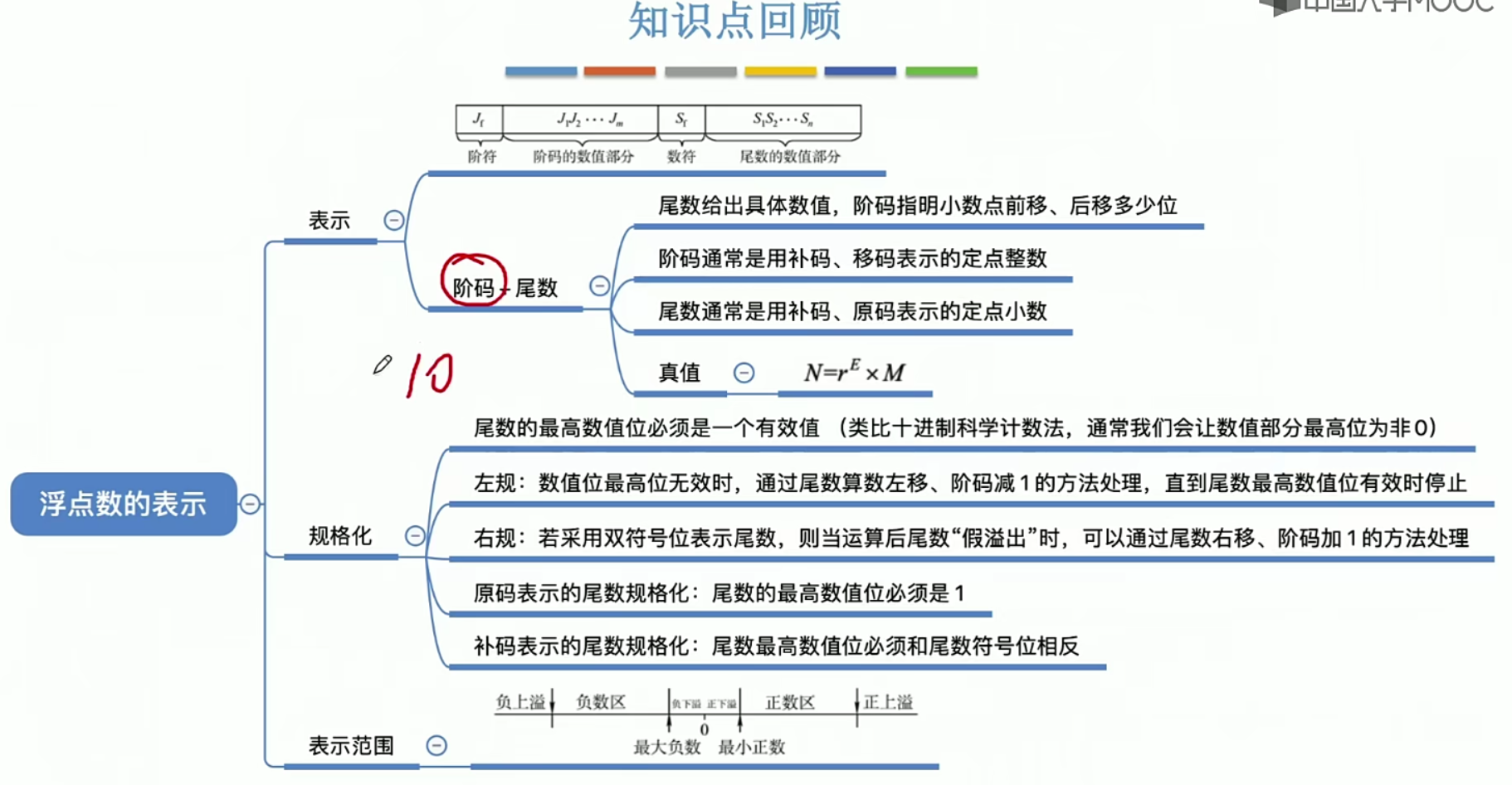
2.9.3规格化浮点数的特点

小结
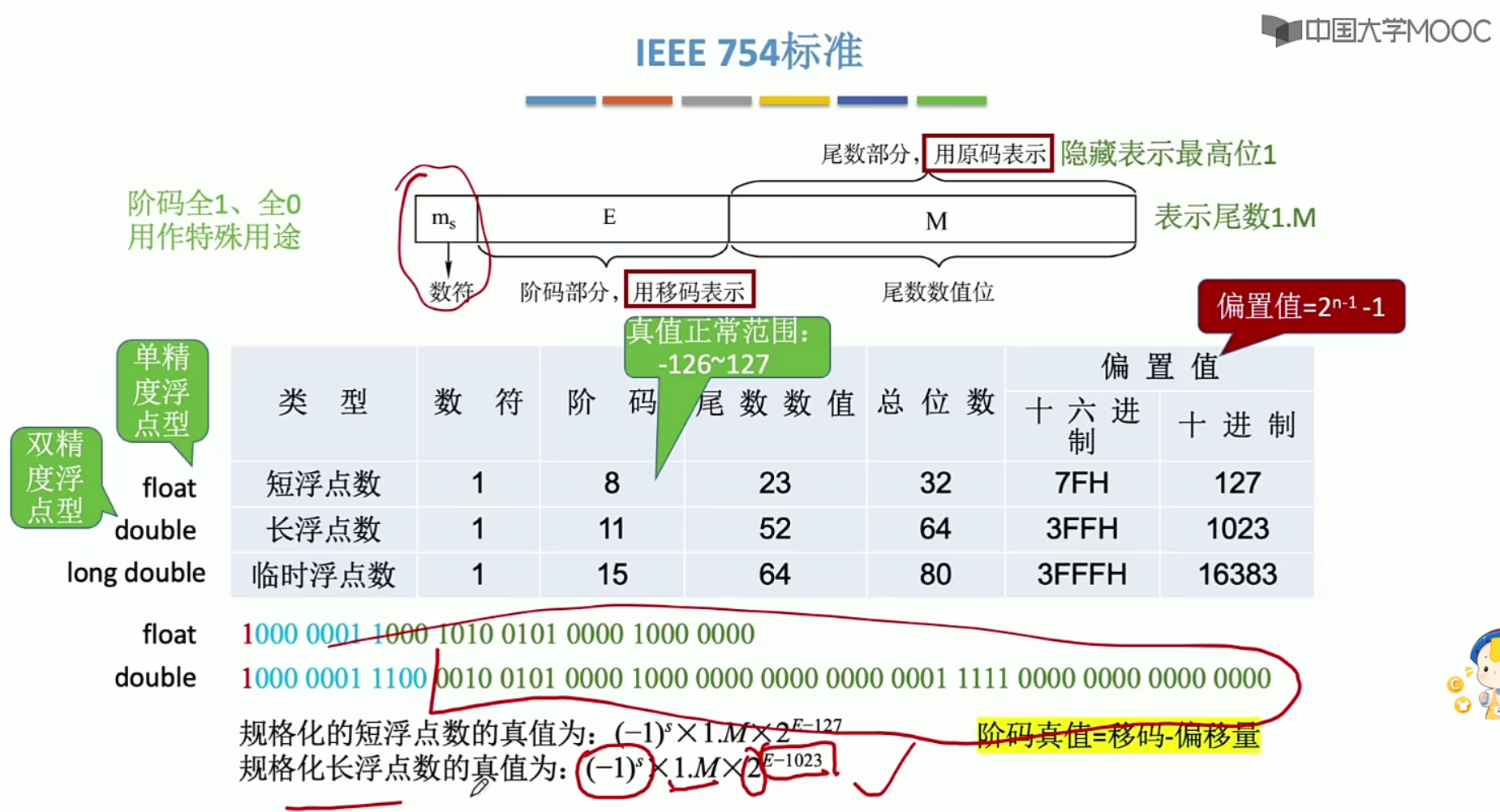
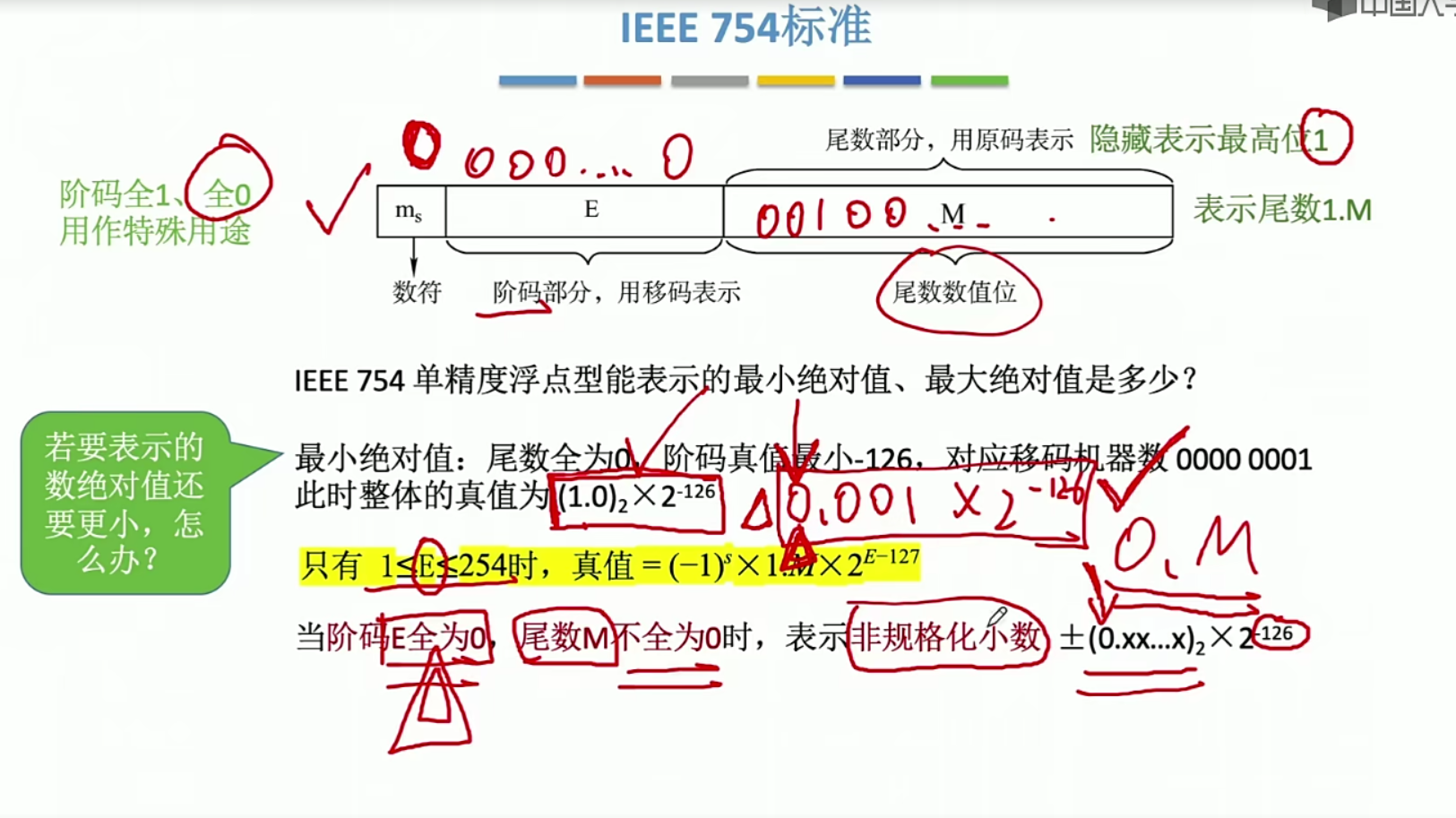
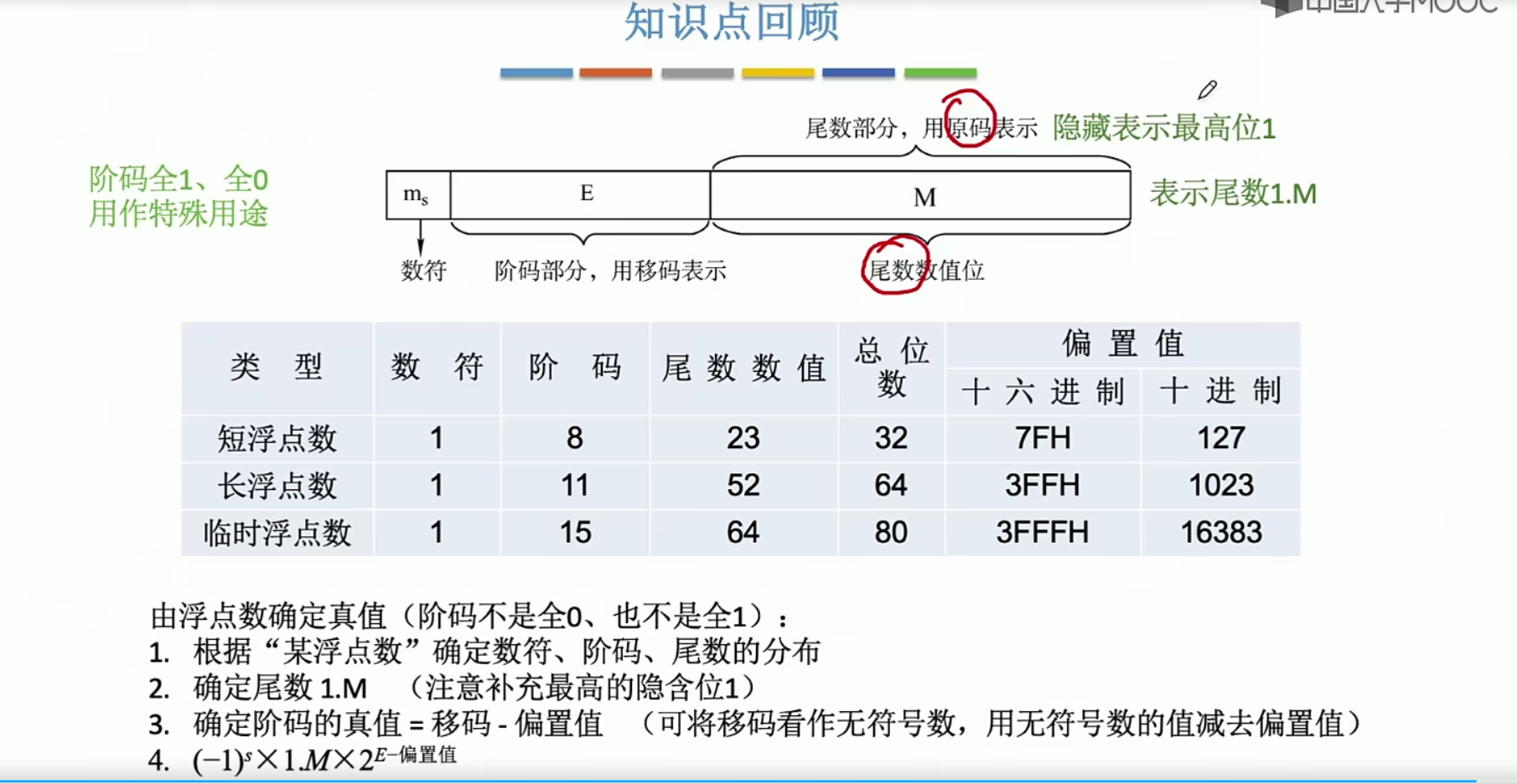
2.10 IEEE标准
正常情况下的移码
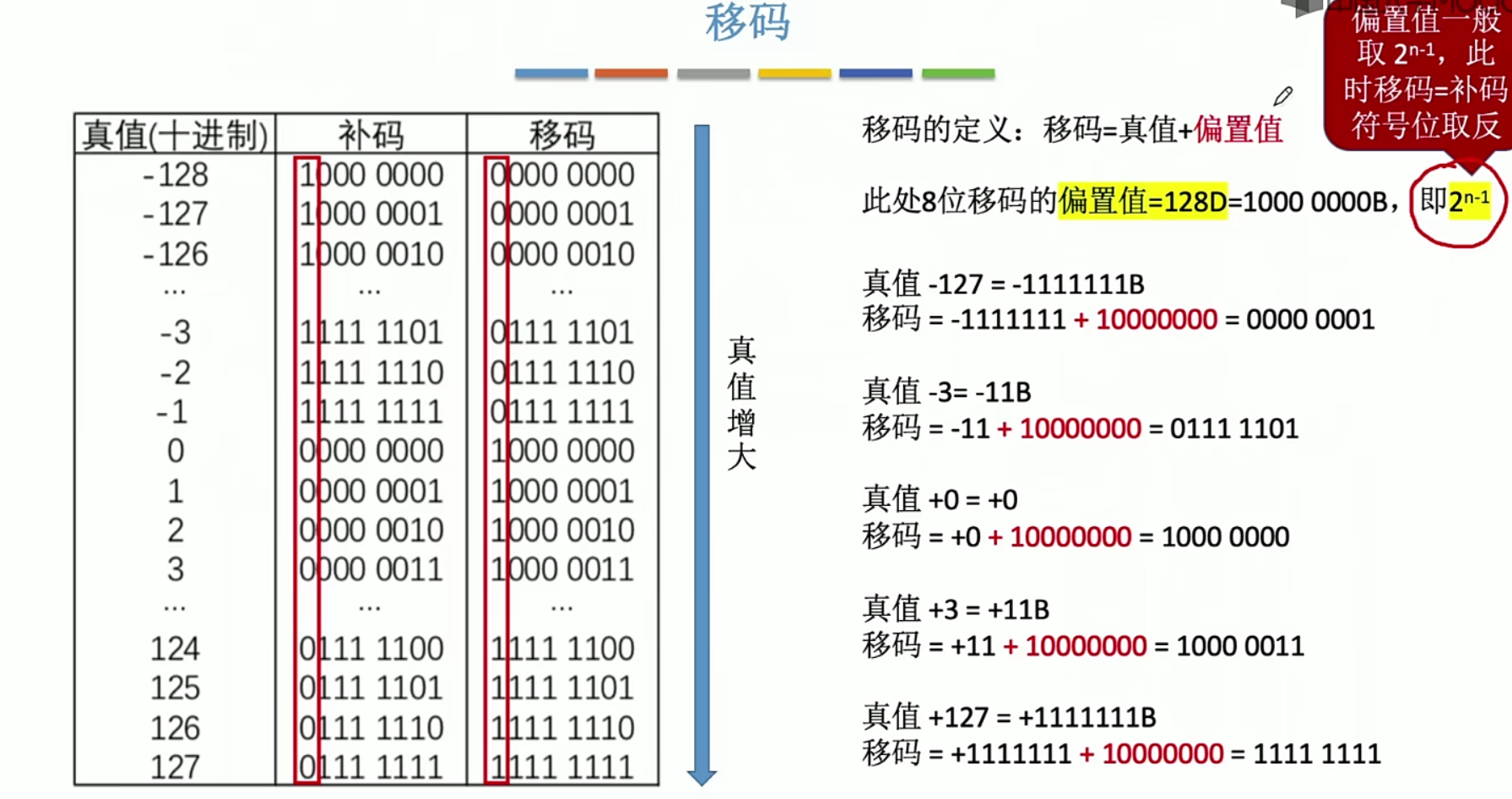
其他情况
IEEE标准
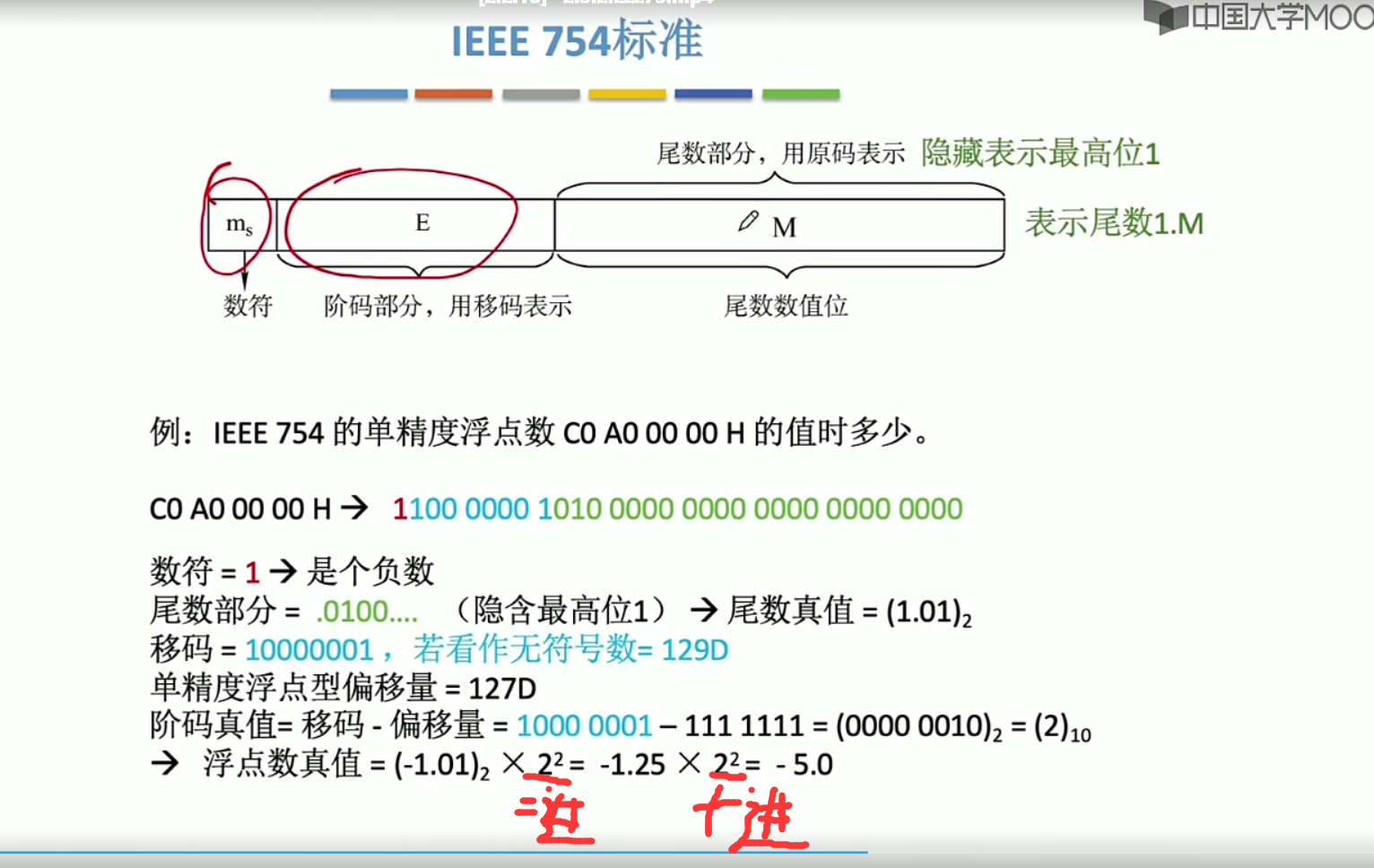
例题

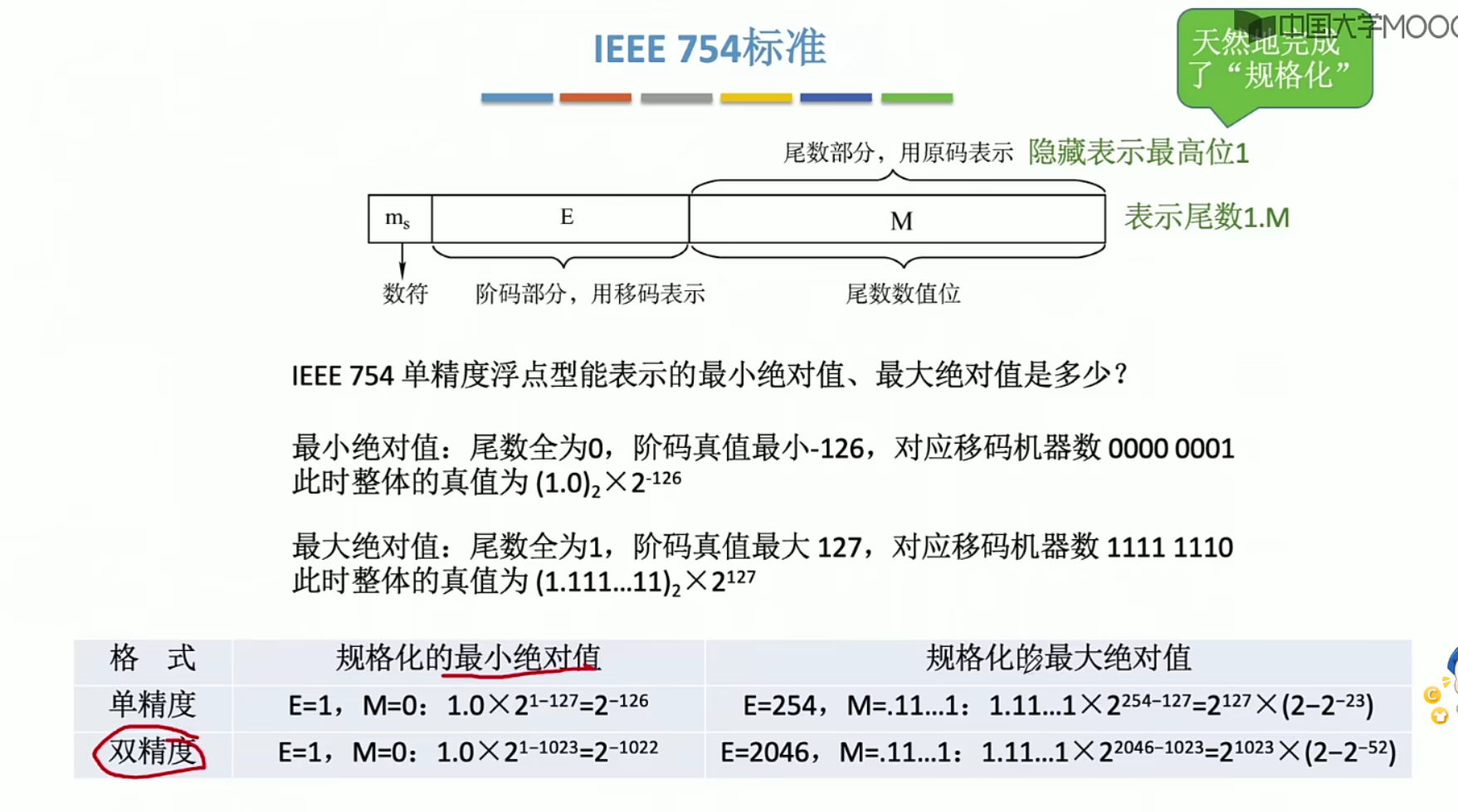
非正常情况

2.11浮点数的运算
步骤
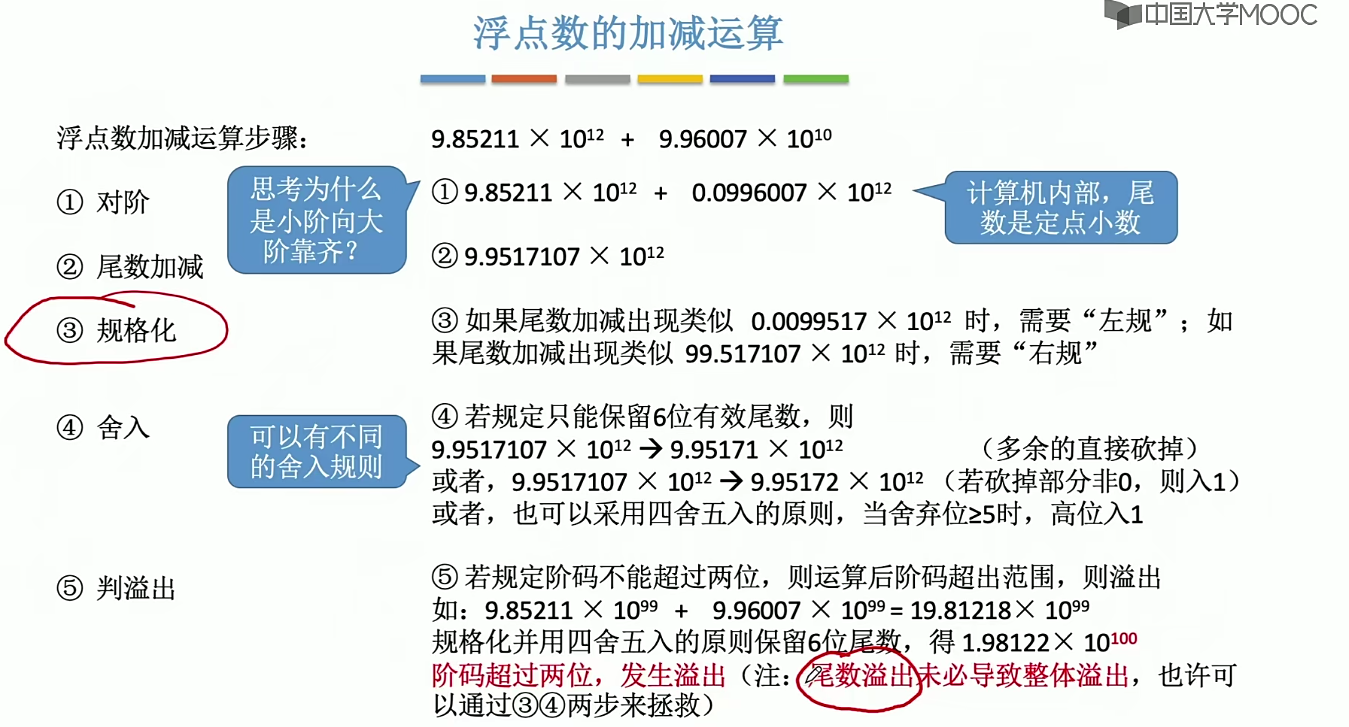
例子


1.对阶

2.3.

4.5


强制类型转换
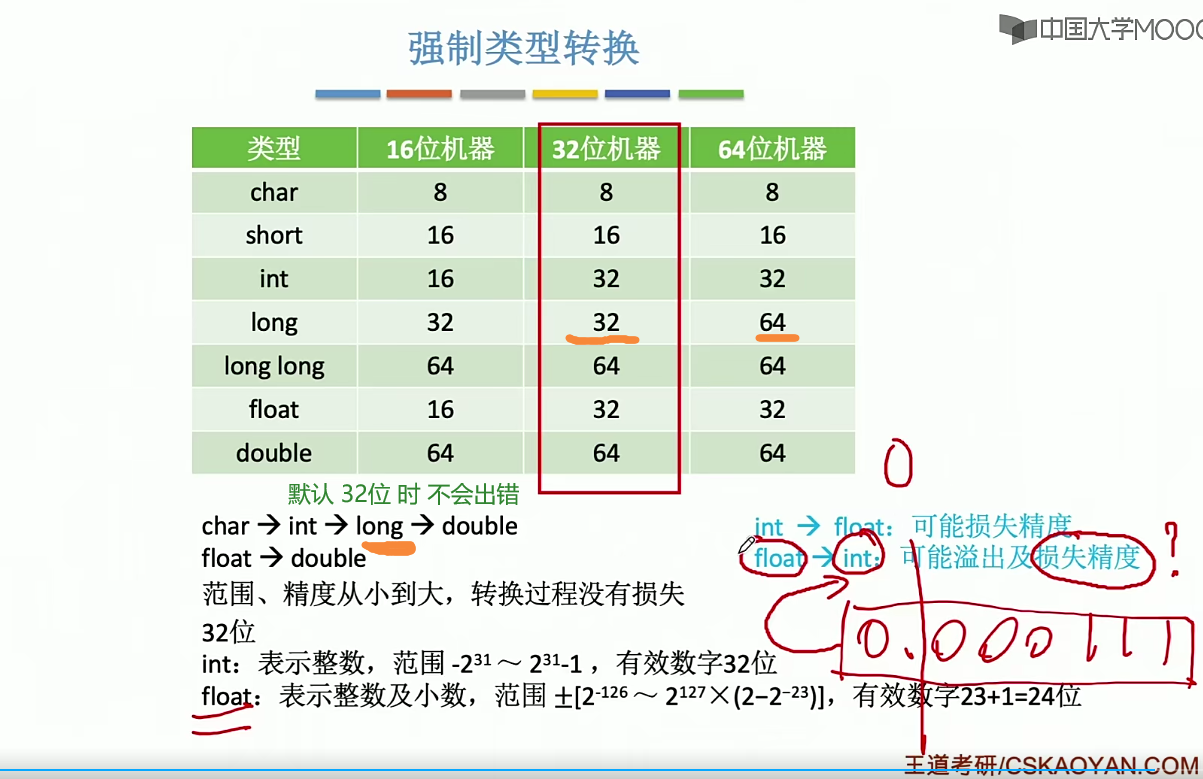
小结
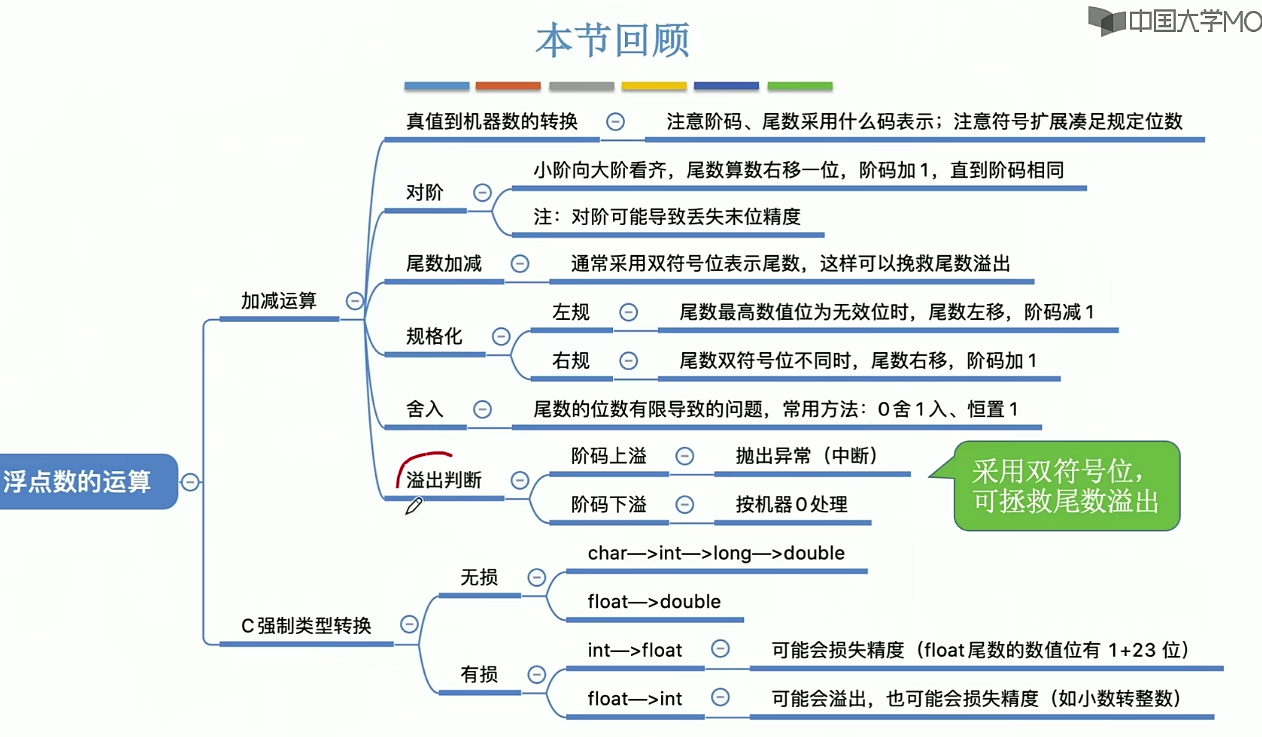
2.12 算数逻辑单元(ALU)
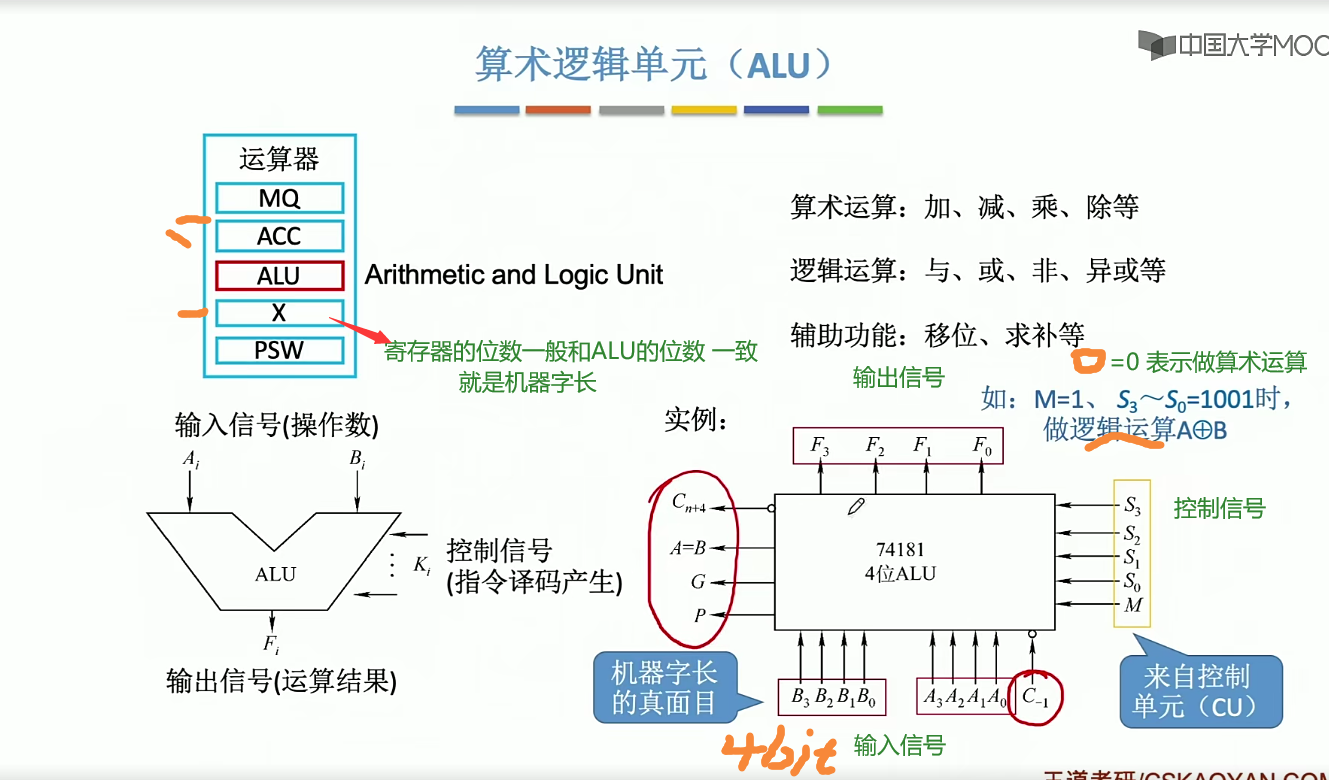
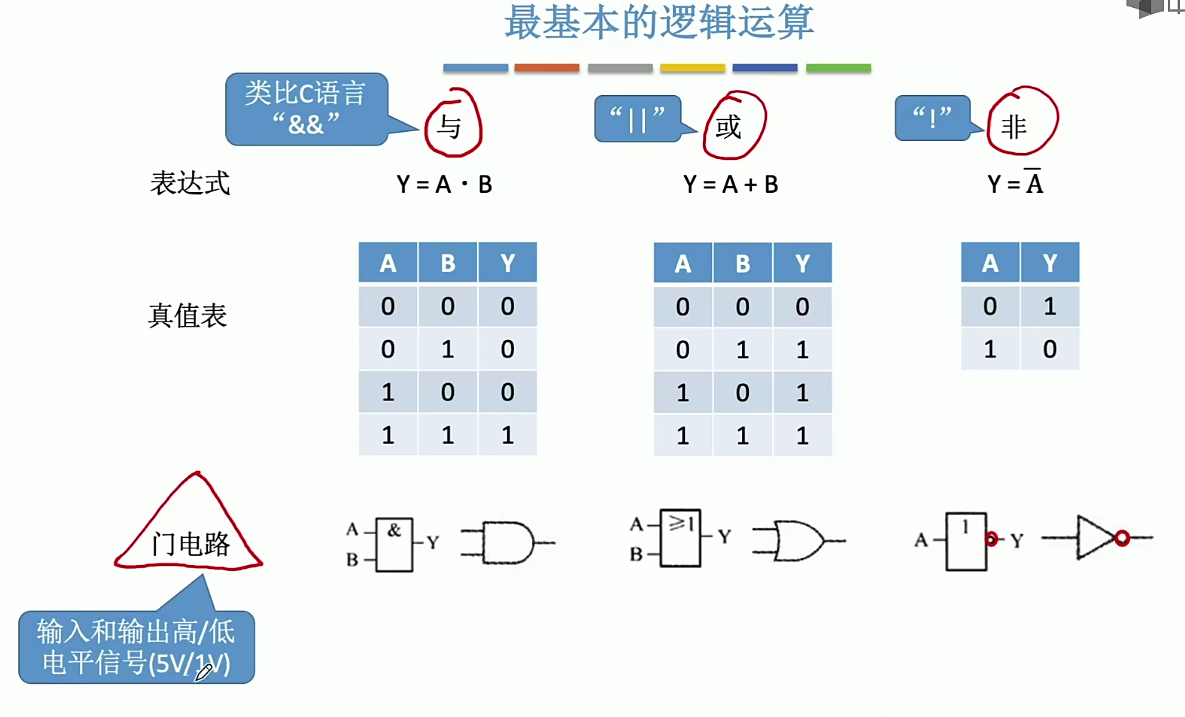
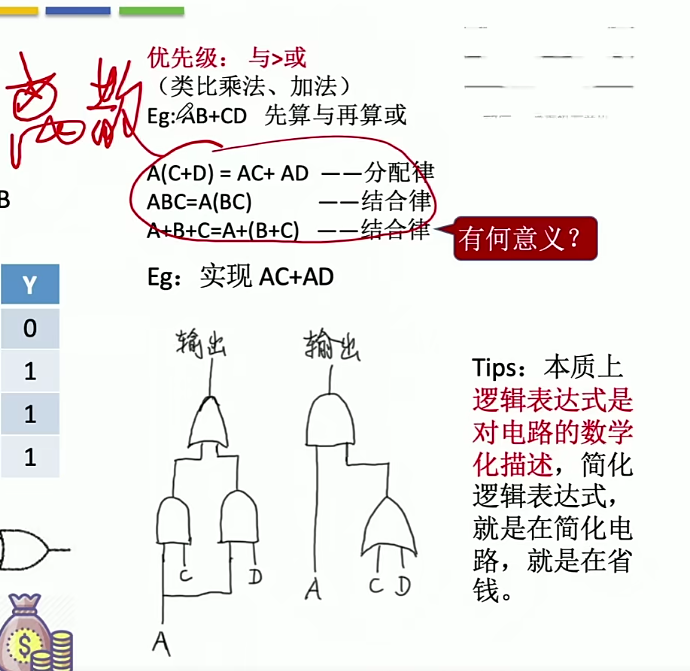
基本的逻辑运算
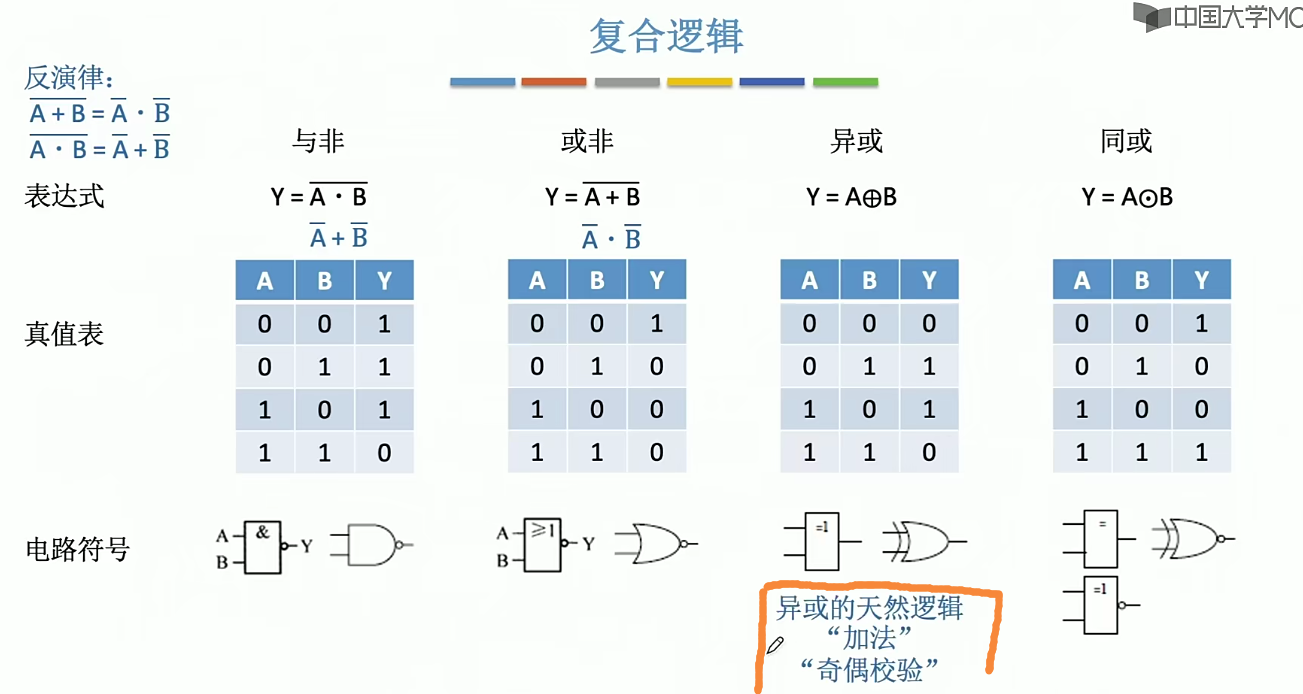
复合逻辑

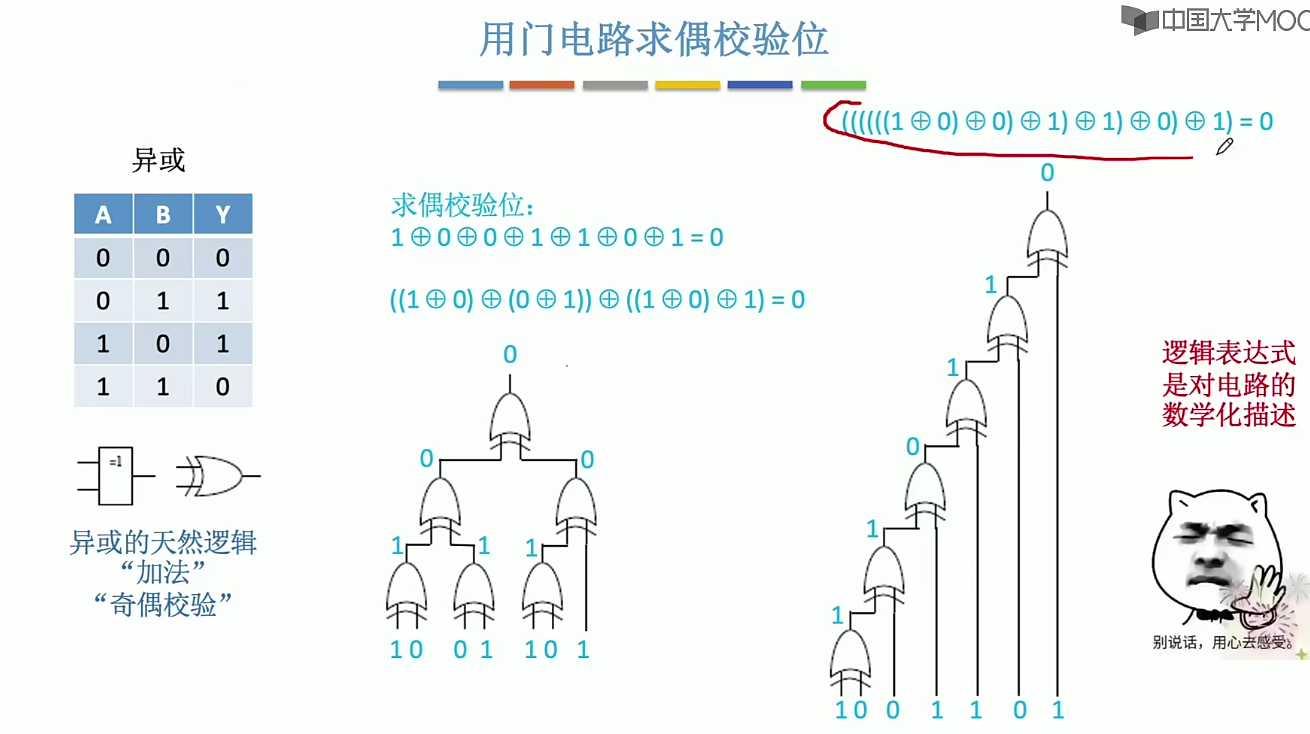
奇偶校验的实现

加法运算
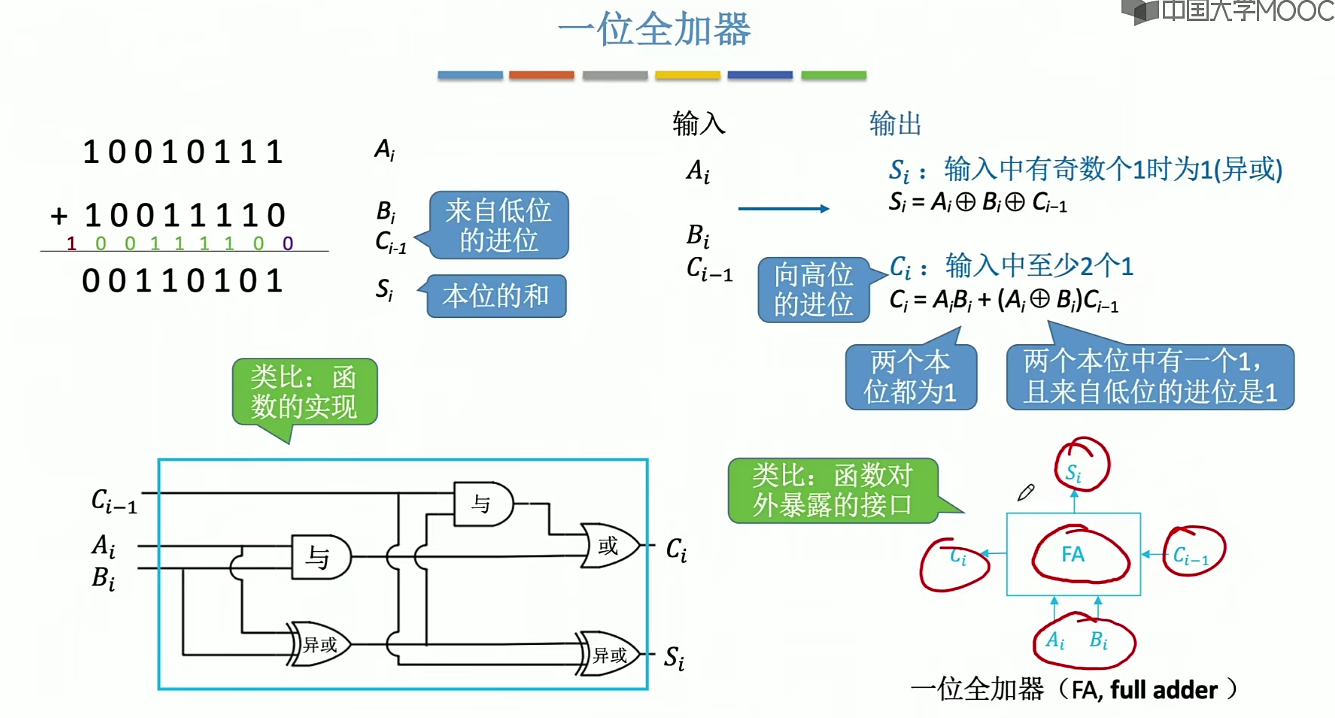
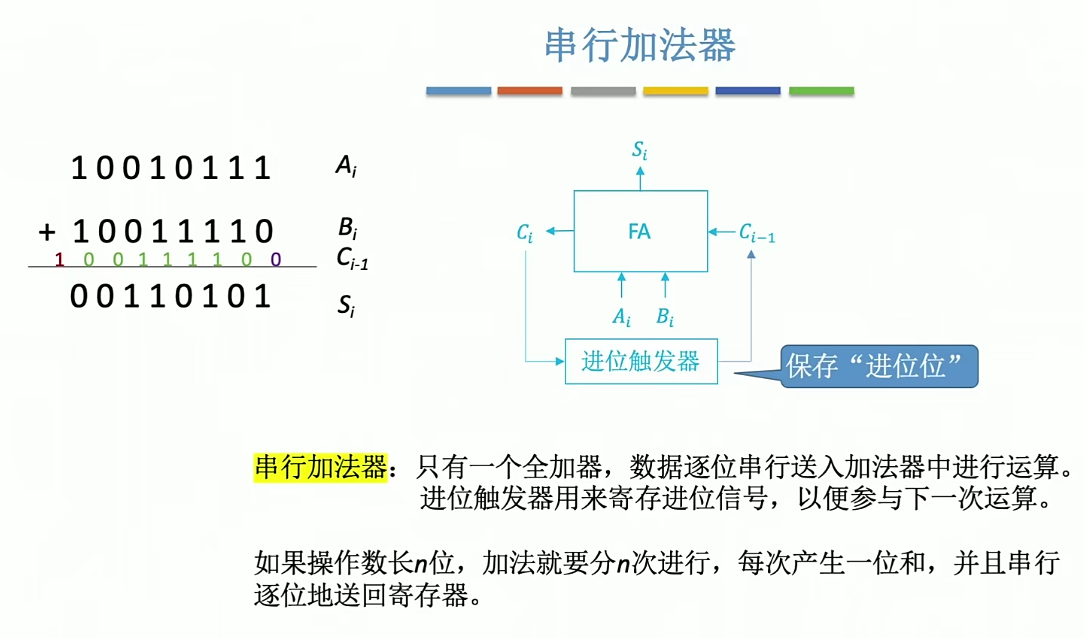
串行加法器
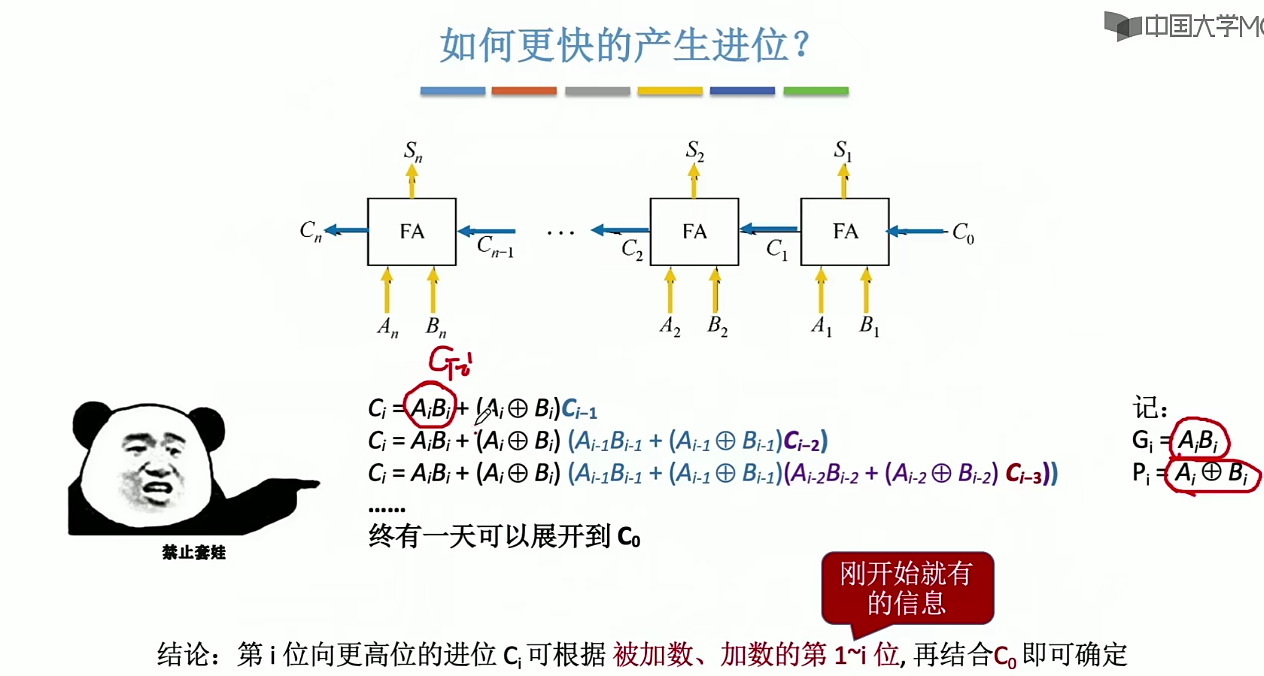
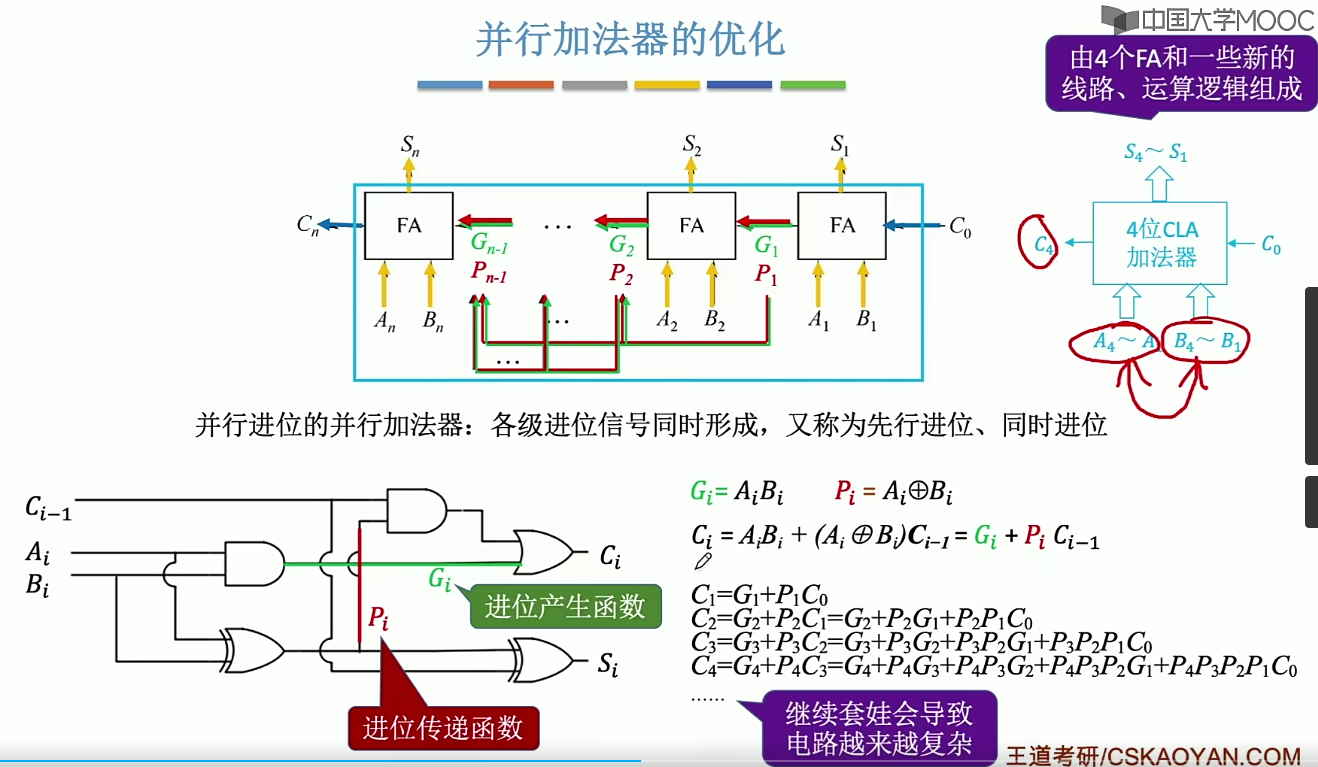
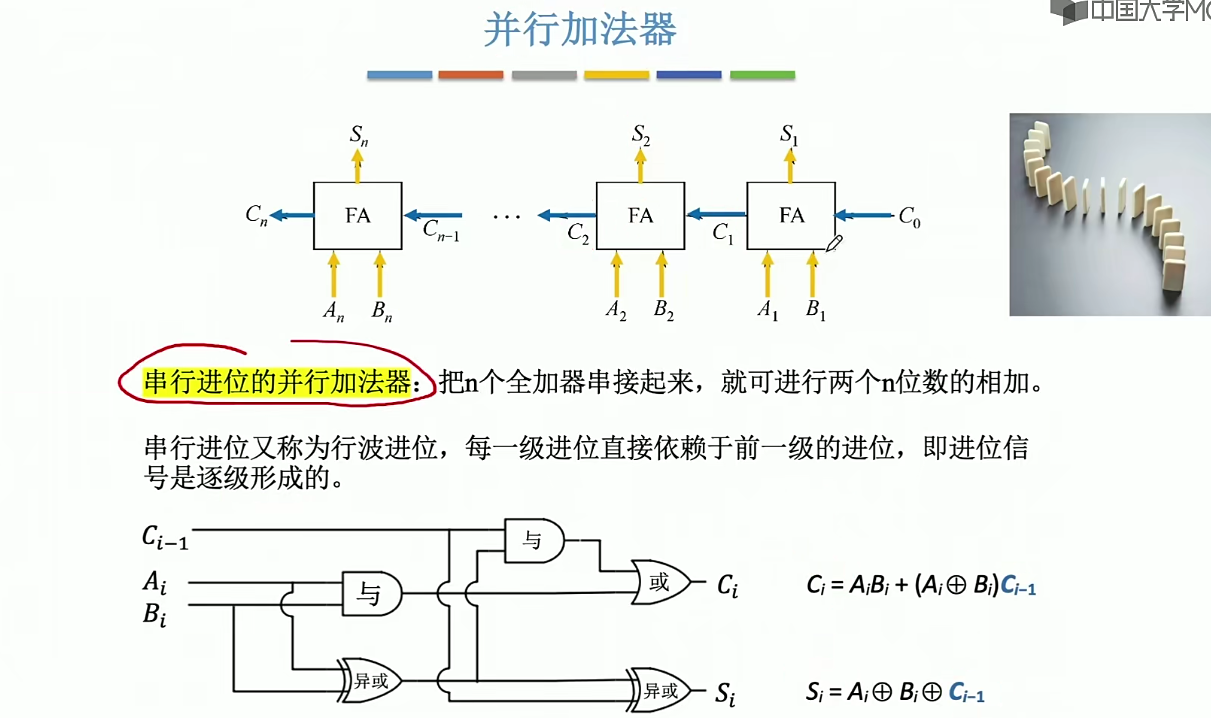
并行加法器
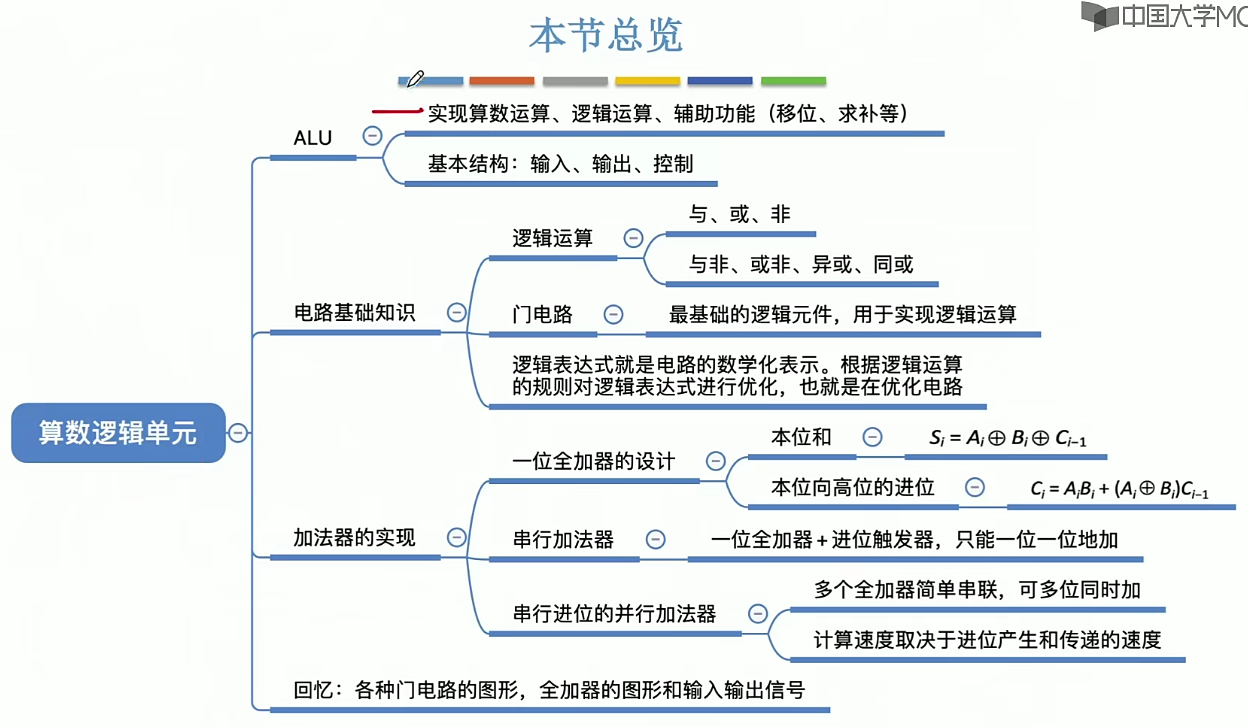
小结
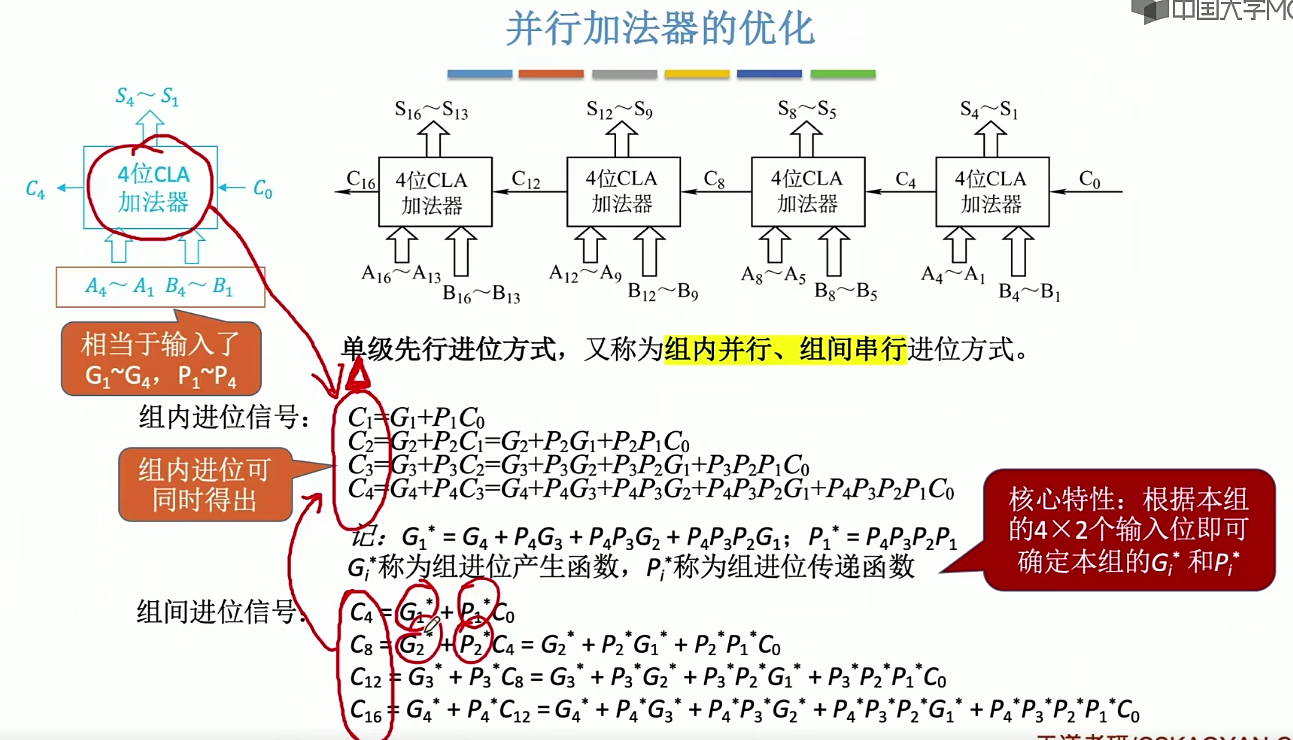
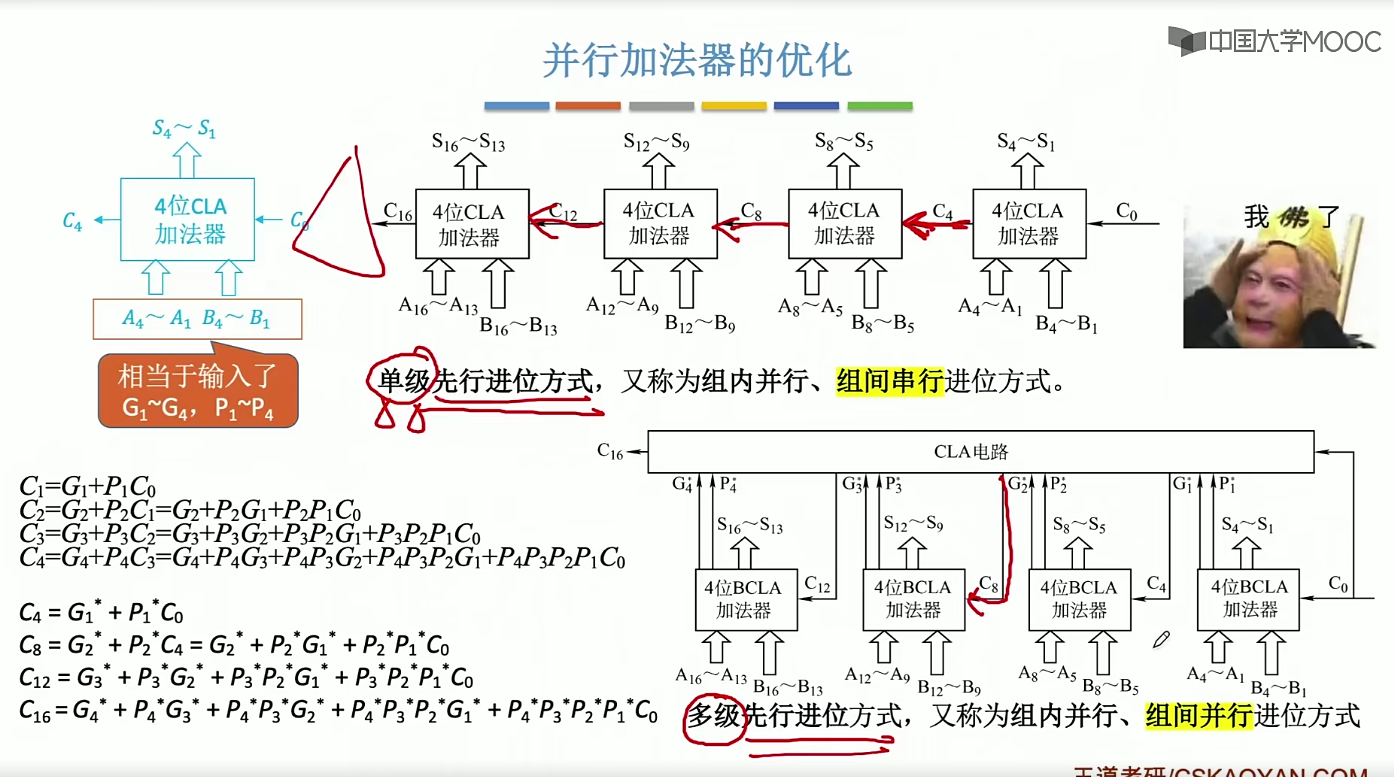
2.13 ALU的改进