Educational Codeforces Round 85 (Rated for Div. 2) E. Divisor Paths 数论

https://codeforces.ml/contest/1334/problem/E

给出一个整数 D，构建一个无向图，满足以下条件：

1.每个顶点都是D的约数（包括1和它本身）；

2.对于两个点x和y，x%y==0 且x/y等于素数 (y%x==0且y/x等于素数)，那么x和y之间存在一条无向边；

3.边权为是x的因子但不是y的因子的个数（x>y).

q次询问，询问两个顶点u，v之间边权和最小的路径数mod998244353，u，v为D的因子。

 D (1≤D≤10¹⁵)，q (1≤q≤3⋅10⁵)， 1≤v,u≤D。

例如 D=12：

 

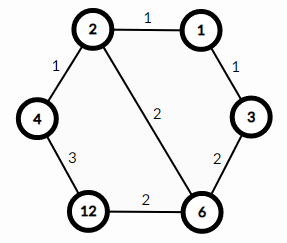
12 -> 2的最小路径有2两条，1 -> 12的最小路径有三条。

思路：1.思考u -> v的最短路径怎么求：

首先u和v如果能相互整除（这里假设u>v)，那么u到v的最短路径只能经过u不断的除 （u/v 的质因数）的点，如果除的数不是（u/v 的质因数），那么必定会再乘一定的数才会到v点，这样路径长度就会增加，什么意思呢？

比如说180 -> 3：180/3=60，60=2² * 3¹ * 5¹那么u->v的路径就只能1：180-> 180/2 =90 -> 90/2=45 -> 45/3=15 -> 15/5=3; 2:180-> 180/2=90 -> 90/3=30 -> 30/5=6 ->6/2=3;3: 180-> 180/3=60 -> 60/2=30 -> 30/2=15 ->15/5=3; 4: 180-> 180/3=60 -> 60/2=30 -> 30/5=6 ->6/2=3;......

这样，u->v的路径长度就是u的因子数减v的因子数，这是最短的，要从u->v必定会除（u的质因子去掉v的质因子）的那些数；那我如果不这样走，除了一个其他质因数，就不能直接除到v还要乘一定的数，路径就会变长，可随便举例，如上图D=12那个，u=12,v=6,只能走 12 -> 12/2=6 ;如果你除一个3，12 -> 12/3=4 ，4只能除2，就不能到3了，只能继续除或者乘一个，这个过程肯定会使路径变长。（严格证明不会，博客写着写着发现这题还没有彻底理解，，，）

如果u和v不能整除，那么他们的路径肯定会经过gcd(u,v)这个点，这样才能找到u和v都能整除的点，才能连通整条路径。然后按照上面可以整除的方法就可以找到最短路径了。

可以整除和不能整除的情况都可以通过u->gcd(u,v)->v 来走，可以整除的话，gcd(u,v)=v，所以两种情况合并。

2：思考怎么求路径数：

通过前面的180->3的例子可以看出，u->gcd(u,v)的路径与（ u/gcd(u,v) ）的质因数的顺序无关，只要把（ u/gcd(u,v) ）的质因数全除掉就可以了，除的顺序任意，那么问题就转换为（ u/gcd(u,v) ）的质因数的全排列，其中有相同的数字。

有两个方法：

1：举例更加直观：g=a1^l1*a2^l2*a3^l3*a4^l4*a5^l5  ,ans=A( l1+l2+l3+l4+l5 , l1+l2+l3+l4+l5 ) / [A( l1 , l1 ) * A( l1 , l1 ) * A( l1 , l1 ) * A( l1 , l1 ) * A( l1 , l1 ) ]也就是 幂的和 的阶层 除以 幂的阶层 的积。

2：ans=ans*C（当前素因子集合，要去除的素因子个数），比如g=a1^l1*a2^l2*a3^l3 ，ans=C ( l1 , l1 ) * C ( l1+l2 , l2 ) * C ( l1+l2+l3 , l3 ) 。

 方法1代码：

#include <bits/stdc++.h>
using namespace std;
const int MAXN=4e5+5;
const long long mod=998244353;
typedef long long ll;
//typedef __int128 LL;
const int inf=0x3f3f3f3f;
const long long INF=0x3f3f3f3f3f3f3f3f;
ll f[MAXN];
ll p[MAXN];//d的质因数
ll cnt=0;
map<ll,ll>mp;//预处理答案
ll quieck_pow(ll a,ll n)
{
    ll ans = 1;
    while(n)
    {
        if(n&1)ans=ans*a%mod;
        a=a*a%mod;
        n>>=1;
    }
    return  ans;
}
ll inv(ll x)
{
    return quieck_pow(x,mod-2);
}
 
ll cal(ll a)
{
    ll ans=1;
    ll sum=0;
    for(int i=1;i<=cnt;i++)
    {
        int t=0;
        while(a%p[i]==0)
        {
            t++;
            a/=p[i];
        }
        if(t)ans=ans*inv(f[t])%mod;
        sum+=t;
    }
    if(a!=1)sum++;
    ans=ans*f[sum]%mod;
    return ans;
}
int main()
{
    f[0]=1;
    for(ll i=1;i<=205;i++)f[i]=f[i-1]*i%mod;
 
    ll d;
    scanf("%lld",&d);
    ll d1=d;
    for(ll i=2;i*i<=d;i++)
    {
        if(d1%i==0)p[++cnt]=i;
        while(d1%i==0)d1/=i;
    }
    if(d1!=1ll)p[++cnt]=d1;
    for(ll i=1;i*i<=d;i++)
    {
        if(d%i==0)
        {
            mp[i]=cal(i);
            mp[d/i]=cal(d/i);
        }
    }
    int q;
    scanf("%d",&q);
    while(q--)
    {
        ll u,v;
        scanf("%lld%lld",&u,&v);
        ll g=__gcd(u,v);
        ll ans=mp[u/g]*mp[v/g]%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
const int MAXN=4e5+5;
const int mod=998244353;
typedef long long ll;
//typedef __int128 LL;
const int inf=0x3f3f3f3f;
const long long INF=0x3f3f3f3f3f3f3f3f;
ll f[MAXN];
map<ll,ll>mp;
ll quieck_pow(ll a,ll n)
{
    ll ans = 1;
    while(n)
    {
        if(n&1)ans=ans*a%mod;
        a=a*a%mod;
        n>>=1;
    }
    return  ans;
}
ll inv(ll x)
{
    return quieck_pow(x,mod-2);
}
 
ll cal(ll a)
{
    //ll tmp=sqrt(a);不要用这个，T成sb了，查了两个小时的错，交了一堆代码，草草草，，，，
    ll ans=1;
    ll sum=0;
    for(ll i=2;i*i<=a;i++)
    {
        ll cnt=0;
        while(a%i==0)
        {
            cnt++;
            a/=i;
        }
        if(cnt)ans=ans*inv(f[cnt])%mod;
        sum+=cnt;
    }
    if(a!=1)sum++,ans=ans*inv(f[1])%mod;
    ans=ans*f[sum]%mod;
    return ans;
}
int main()
{
    f[0]=1;
    for(ll i=1;i<=205;i++)f[i]=f[i-1]*i%mod;//预处理出每个数的阶层
 
    ll d;
    scanf("%lld",&d);
    for(ll i=1;i*i<=d;i++)
    {
        if(d%i==0)
        {
            mp[i]=cal(i);
            mp[d/i]=cal(d/i);
        }
    }
    int q;
    scanf("%d",&q);
    while(q--)
    {
        ll u,v;
        scanf("%lld%lld",&u,&v);
        ll g=__gcd(u,v);
        ll ans=mp[u/g]*mp[v/g]%mod;
        printf("%lld\n",ans);
    }
    return 0;
}
 
 

方法2代码：

#include <bits/stdc++.h>
using namespace std;
const int MAXN=4e5+5;
const long long mod=998244353;
typedef long long ll;
//typedef __int128 LL;
const int inf=0x3f3f3f3f;
const long long INF=0x3f3f3f3f3f3f3f3f;

ll p[MAXN];//存d的素因子
int cnt=0;

ll fac[MAXN],invfac[MAXN],inv[MAXN];
void init(int n)
{
    invfac[0]=1;
    fac[0]=1;
    inv[1]=1;
    for(int i=2;i<=n;++i) inv[i]=((mod-mod/i)*inv[mod%i])%mod;
    for(int i=1;i<=n;++i) fac[i]=fac[i-1]*i%mod,invfac[i]=invfac[i-1]*inv[i]%mod;
}
ll C(int n,int m)
{
    return fac[n]*invfac[m]%mod*invfac[n-m]%mod;
}

ll solve(ll u)
{
    ll ans=1,sum=0;
    for(int i=1;i<=cnt;i++)
    {
        int sum1=0;
        while(u%p[i]==0)sum1++,u/=p[i];
        sum+=sum1;
        if(sum1)ans=ans*C(sum,sum1)%mod;
    }
    return ans;
}
int main()
{
    init(205);
    ll d;
    scanf("%lld",&d);
    for(ll i=2;i*i<=d;i++)
    {
        if(d%i==0)p[++cnt]=i;
        while(d%i==0)d/=i;
    }
    if(d!=1ll)p[++cnt]=d;

    int q;
    scanf("%d",&q);
    while(q--)
    {
        ll u,v;
        scanf("%lld%lld",&u,&v);
        ll g=__gcd(u,v);
        u/=g;
        v/=g;
        ll ans=solve(u)*solve(v)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

 

PS：这题写得我超自闭，自己想了很久，不会，然后看官方题解，看不懂，是一点都不知道在讲啥，英语不好，翻译后又贼奇怪，一个一个单词翻译看不懂，一句一句翻译看不懂，这可能就是菜鸡看英文的日常；然后搜博客，一篇看不懂，再来一篇还是看不懂，很模糊，没有思路，没办法，只有那几篇博客，于是一篇一篇挨着仔细看，对于同一个问题点几篇博客对照着看，一点一点理解，然后每个点都理解了很久，然后忘了排列组合怎么求，也想了很久，太菜了，啊啊啊啊啊，，写完代码交的时候，我tm交了一个小时还在queue，（可能昨晚的D3在测？）这段时间在写另一种解法，然后当结果出来tle，，，心态有点崩，我按照博客的思路写的，虽然不是一模一样，但思路是一样的，复杂度也还行，极度怀疑博主的代码不能AC，在演我，交了一发，AC，一瞬打脸，草；然后看了一万年的代码，emmm，换个组合数板子试下？？好了，AC，心中万马奔腾🐎🐎🐎草草草，，，然后另一种解法也是tle，我今天一定和tle有仇，改了各种，写了各种代码，所幸有些代码AC了，但我就是搞不懂，我和博客写得一样的解法就是不能A，草，为什么，我姿势哪里不对了？？？？？？最后没办法，乱改，把sqrt改成 i*i<=a，就A了？？？？我的sqrt明明写在for循环的外面的，平时也都这么写的，学长也这样教的，让我的认知出现了颠覆，可能这题调用函数比较多？算了很多次？？但我寻思一个小与等于1e7的数的因素应该不是太多吧？？sqrt复杂度到底有多高？？迷惑，，以后为了保险还是写 i*i<=a 吧，，，，，然后试了很多写法，看运行时间能不能再短点。

总之，题很好，让我换了个快一点的组合数板子，还有把sqrt写法改成i*i<=a。（菜逼AC心路，补题补了一个晚上+一天，博客写着写着发现不能严格证明出结论，伤心）

附上一张交题截图（证明我的菜证明我的心酸 ：