Codeforces Round #632 (Div. 2) E. Road to 1600 思维or构造

https://codeforces.com/contest/1333/problem/E

定义一个 n*n 的国际棋盘，车只能上下左右移动，皇后可以上下左右和斜对角线移动，可以移动任意距离，如下图所示：

n*n的棋盘上有1~n² 的数，且互不相同，一开始车和皇后都在数字为1的单元上（单独的一张棋盘上移动），且数字为1的这个单元被访问过了，它有以下移动规则：

1.该图所有可以移动但尚未被访问的单元中，数值最小的单元；

2.所有可移动的单元都被访问过了，则被传送到数值最少的未被访问的单元，执行该步需要1的花费；

3.所有单元格都要被访问。

要求找到n*n的棋盘，满足车的花费严格小于皇后的花费（不能都不花费），如果不存在则打印 -1.

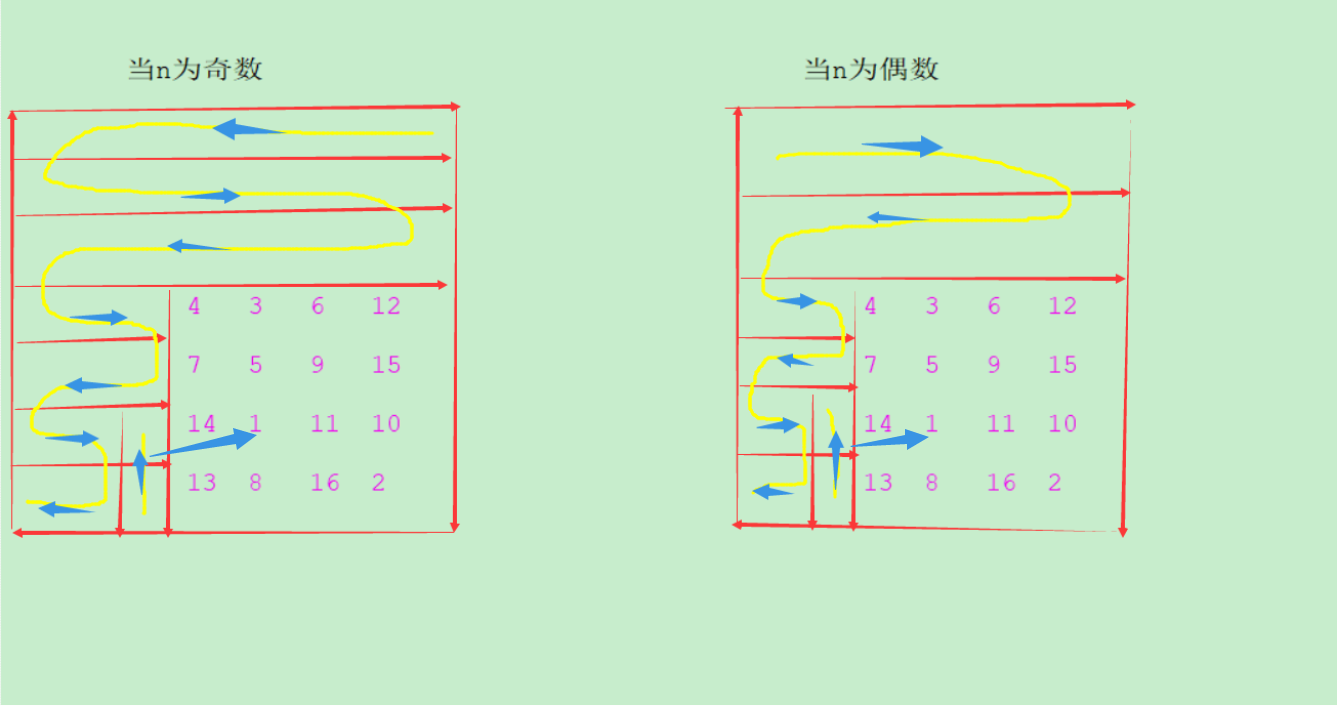
想了很久，画不出来，后来灵光一闪，案例给了一个n=4的棋盘，那我就利用那个棋盘的相对大小，把它放在右下角，让其余的棋子车和皇后的走法都一致，那这些移动的花费就都一致，其实就是0，然后在右下角接上案例给的棋盘，接的位置必须和棋盘里最小的那个数同一排，然后直接跳到最小位置，就和小棋盘的走法一样了，就可以满足了，n<3棋盘是肯定不存在的，做题的时候以为n=3也不存在，所以wa了一发，然后我就直接特判3了，没有再重写代码，所以代码可能有点丑~~ （要是案例没有的话，就暴力一个出来也是可以的） 具体做法和代码如下：

#include <bits/stdc++.h>
using namespace std;
const int MAXN=5e5+5;
const int mod=1e9+7;
typedef long long ll;
//typedef __int128 LL;
const int inf=0x3f3f3f3f;
const long long INF=0x3f3f3f3f3f3f3f3f;

int a[505][505];
int main()
{
    int n;
    scanf("%d",&n);
    if(n<=3)
    {
        if(n<3)printf("-1\n");
        else
        {
            printf("%d %d %d\n",1,7,9);
            printf("%d %d %d\n",3,2,5);
            printf("%d %d %d\n",4,8,6);
        }
    }
    else
    {
        int k=0;
        //前面部分
        for(int i=1;i<=n-4&&n-4>0;i++)
        {
            if((n-4)%2==0)
            {
                if(i%2)for(int j=1;j<=n;j++)a[i][j]=++k;
                else for(int j=n;j>=1;j--)a[i][j]=++k;
            }
            else
            {
                if(i%2==0)for(int j=1;j<=n;j++)a[i][j]=++k;
                else for(int j=n;j>=1;j--)a[i][j]=++k;
            }

        }

        //右下角小正方形的左边部分
        for(int i=1;i<=n-4;i++)a[n-3][i]=++k;
        for(int i=n-4;i>=1;i--)a[n-2][i]=++k;
        for(int i=1;i<=n-5;i++)a[n-1][i]=++k;
        for(int i=n-5;i>=1;i--)a[n][i]=++k;
        a[n][n-4]=++k;
        a[n-1][n-4]=++k;

        //右下角的小正方形
        k=n*n-16;
        a[n-1][n-2]=++k;
        a[n][n]=++k;
        a[n-3][n-2]=++k;
        a[n-3][n-3]=++k;
        a[n-2][n-2]=++k;
        a[n-3][n-1]=++k;
        a[n-2][n-3]=++k;
        a[n][n-2]=++k;
        a[n-2][n-1]=++k;
        a[n-1][n]=++k;
        a[n-1][n-1]=++k;
        a[n-3][n]=++k;
        a[n][n-3]=++k;
        a[n-1][n-3]=++k;
        a[n-2][n]=++k;
        a[n][n-1]=++k;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)printf("%d%c",a[i][j],j==n?'\n':' ');
    }
    return 0;
}