一维数组
对于一个一维数组a[10]来说
它对储存空间的申请可以看成是这样的

数组名a就代表着首元素a[0]的地址,也很容易看出a+5是元素a[5]的地址。
二维数组
对于一个二维数组a[3][2]来说
它对储存空间的申请可以看成是这样的
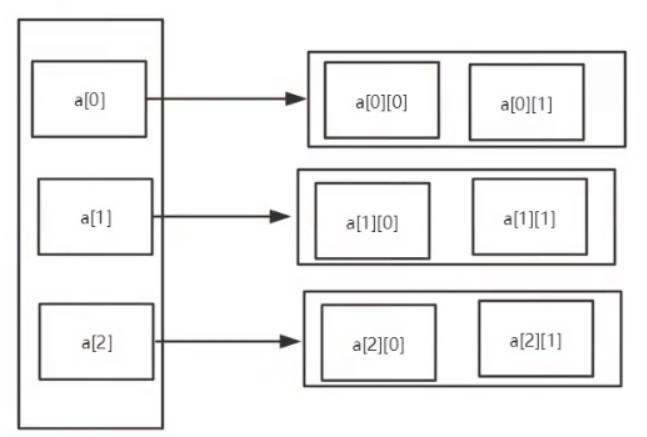
可以很容易的知道a[0][1]便是它的一个元素,a[0]便是它的一个元素地址,a便是它的行地址。
所以可以发现对于二维数组中的,a----a[0]-----a[0][1],它们是以行地址---元素地址---元素的值,这三个级别每有一个[]就降一个级别
对于出现数据类型的判断便变得容易了,比如说:
a 没有出现[],就便是最高级别行地址
a[] 出现了一组[],便降低了一个级别变成了元素地址级别
a[][] 出现了两组的[],便降低了两个级别变成了元素的值级别
那么如在其后加上常数i变成了a+i,a[0]+i,a[0][1]+i呢?
我们可以把它看为两个部分,一个是类型,一个是常数,
对于a[0]+i来说,可以看成两个部分,一个是a[0],一个是+i,可以先判断a[0],我们可以知道它是一个元素地址,对于图表上来说就是a[0]这一格,再看常数i,
它具有继承性,也便是对a[0]+i,因为a[0]是一个元素地址,所以加的这个i的单位也别是元素地址了,所以a[0]+i也便是a[0]向后移动i格的地址。
那如果是a+i,这个i的单位也便是行地址了,所以a+i表示的是第i行的行地址。
同样的*也是这个效果。
ps
其实我更喜欢这么理解一维数组的元素是单纯的元素,而二维的数组的元素就是一维数组,对于二维数组b[2][3]可以看成这样
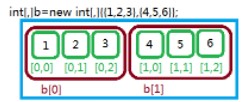
它是由两个一维数组b[0]和b[1]所组成。b[0]和b[1]中都有三个元素。
因为数组名表示的是首元素的地址,所以b代表的是b[0](二维数组的元素是一维数组)这个数组的地址,也便是行地址,而b[0]可以看成一维数组的数组名,
因为数组名是数组首元素的地址,所以b[0]便是名为"b[0]",的数组的首元素b[0][0](可以看成一个叫b[0]的一维数组)的地址,也别是元素地址了。
其实三维数组也是这样的,可以试试。



