Coursera-AndrewNg(吴恩达)机器学习笔记——第二周

一.多变量线性回归问题（linear regression with multiple variables）

1. 搭建环境Octave
   Windows的安装包可由此链接获取：https://ftp.gnu.org/gnu/octave/windows/，可以选择一个比较新的版本进行安装，本人win10操作系统，安装版本4.2.1，没有任何问题。注意不要安装4.0.0这个版本。当然安装MATLAB也是可以的，我两个软件都安装了，在本课程中只使用Octave就已经足够用了！
   
2. 符号标记：n（样本的特征数/属性数目），表示第i个训练样本的第j个特征。样本可能有多个属性值，在房价预测案例中，可能有多种因素如房屋大小、楼层、装修程度等共同决定最终房价。

3. 预测函数（Hypothesis）：h_θ(x)=θ₀+θ₁x₁+θ₂x₂+……+θ_nx_n，记x₀=1（）
   
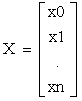
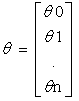
   所以预测函数使用矩阵相乘的形式可写为：h_θ(x)=Θ^TX.

4.  代价函数（Cost Function）形式：其中参数θ_n的数目和特征数n相同。

   

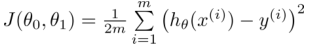
5. 梯度下降算法：（注意同时更新所有θ值）
   
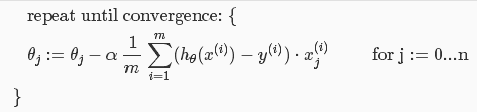
6. Feature Scaling（特征缩放）：确保各个特征的取值近似，否则收敛速度会很慢。建议：将所有特征取值近似缩放到[-1,1]之间，当然也不必特别精准，只是为了梯度下降运算速度更快。
   方法（Mean Normalization）：x_i=(x_i-μ_i)/s_i，μ_i是x_i的平均值，s_i是x_i的标准差或者是x_i的范围（x_max-x_min）。x₀不需要进行特征缩放，因为我们在前面将x₀记为1。
7. 学习速率α：α过大，梯度下降难以收敛，代价函数J(θ)甚至会变大。α过小，梯度下降收敛速度慢。如何判断已经收敛：两次迭代代价函数J(θ)差值是否小于某一个阈值（不好找）。
8. 正规方程（Normal Equation）：求解θ的解析方法，该方法不需要做特征缩放。
   公式如下：θ=(X^TX)^-1X^TY                   Octave代码：pinv(X`*X)*X`*Y，或者使用inv函数
   正规方程和梯度下降方法求解θ特点：不需要选择学习速率α，不需要进行迭代求解。当特征数目n>10⁶很大时，梯度下降可以很好的求解，但是正规方程的求解速度将会很慢。
   当存在冗余的特征，十分的接近的特征或者特征过多（n>m）时，X^TX会不可逆，这时使用Octave的pinv函数依旧可以求出结果。

二.Octave的简单使用

• 变量的赋值

%后内容表示注释　　~=为不等号　　&&逻辑与　　||逻辑或　　xor( , )逻辑异或　　format long/short控制输出格式
PSI('>>'); %简化命令行显示
a=3 %变量赋值
a=3; %末尾;可以抑制打印输出
disp(a); %打印变量值，或者直接输出字母a
disp(sprintf('2 decimals: %0.2f',a)) %类似C语言的形式输出两位小数
A=[1 2;3 4;5 6] %定义一个矩阵
V=1:0.1:2 %定义一个1行11列矩阵
C=2*ones(2,3) %定义一个2行3列的矩阵，所有元素都是2
W=zeros(1,3) %定义一个1行3列的矩阵，所有元素都是0
rand(3,3) %随机赋值3*3矩阵
randn(3,3) %随机赋值3*3矩阵，符合高斯分布，平均值为0，方差为1
w=-6+sqrt(9)*(randn(1,1000)); 变量w赋值,w是一个均值为-6，方差为3的矩阵
hist(w) %画直方图，hist为统计函数，默认统计10个区间中，出现w的个数，纵轴值为个数
eye(4)%设置4阶单位矩阵

• 数据的处理

pwd命令显示当前路径　　cd命令转换路径　　ls命令显示文件列表　　who命令显示工作空间中的变量　　whos命令显示变量的详细信息　　
clear features X删除变量X　　导入数据命令load featuresX.dat或load('featuresX.dat')　　clear命令清空工作空间中所有变量
size(A) %求矩阵的维数，返回的值也是一个矩阵，也可用于求向量的维数
length(v) %求向量的维数，一般不用于矩阵
v=priceY(1:10) %将priceY中前10个数据存入v中
save hello.mat v; %将v的数据存入硬盘中，.mat格式文件按照二进制形式存取，占用空间小
save hello.txt v -ascii %将v中的数据按照字符形式进行存储
A(3,2) %矩阵A3行2列的元素值
A(2,:) %矩阵A2行上所有元素的值
A([1 3],:) %矩阵A中1,3行所有元素的值
A(:,2)=[10;11;12] %对矩阵A第二列所有元素重新赋值
A=[A,[1;2;3]] %矩阵A新增一列
A(:) %将矩阵A中元素按列拼接，输出一个向量
C=[A B] %将矩阵A，B左右拼接
C=[A;B] %将矩阵A，B上下拼接
A.*B %矩阵A,B同阶，对应元素相乘
A.^2 %矩阵A中元素做平方
1./A %矩阵A中元素取到数
log(v) %求自然对数，e为底　　exp(v) %求指数　　abs(v) %求绝对值　　A`为A的转置　　pinv(A)为A的逆
val=max(a) %返回向量中的最大值
[val ind]=max(a) %返回向量中的最大值和最大值的索引
a<3 %该操作对向量中的元素逐个进行比较　　find(a<3) %显示满足条件的下标
A=magic(3)%生成一个3*3维的magic matrix，每行每列值的和相等
[r,c]=find(A>7) %返回满足条件的行列向量索引
sum(a) %将向量所有元素值相加　　prod(a) %求向量所有元素值的乘积　　floor(a) %将所有元素指向下取整　　ceil(a) %将所有元素值向上取整
max(A,[],1) %求每列最大值　　max(A,[],2) %求每行最大值　　max(max(A)) %求矩阵A中的最大值，也可写为max(A(:))
sum(A,1) %求矩阵A每列的和　　sum(A,2) %求矩阵A每行的和
sum(sum(A.*eye(9))) %计算对角线值的和　　sum(sum(A.*flipud(eye(9)))) %计算反向对角线的和

•  绘制数据

　　

　　　　　　

 

 　　

• 语句和函数

v=zeros(10,1)
for i=1:10,　　　　%for语句
    v(i)=2^i;
end;

i=1;
while i<=5,　　%while语句
　　v(i)=100;
　　i=i+1;
end;

i=1;
while true,　　%break语句
　　v(i)=999;
　　i=i+1;
　　if i==6,
　　　　break;
　　end;
end;

v(1)=2;
if v(1)==1,　　%if-elseif-if语句
　　disp('the value is one');
elseif v(1)==2,
　　disp('the value is two');
else
　　disp('the value is not one or two')
end;

1. 函数：创建文件，以函数名来命名，以.m后缀结尾。
2. 创建Octave搜索路径：% Octave search path (advanced/optimal)
                                       addpath('c:\Users\ang\Desktop')
   函数文件在该路径下，自动检索。
3. Octave语法中函数可以返回多个值。
4. 向量化：建议计算时进行向量计算，不使用循环。