圆周卷积

圆周运算

其实圆周运算是针对周期序列而言的，由于周期序列在每一个周期内的取值都相同，所以我们只关注它的主值区间，比如，如果一个序列的长度为$N$的话，那么它的主值区间就是$0\leq n\leq N-1$。

虽然圆周运算是源自于对周期信号的处理，但是经过一般化的扩展之后，对有限长序列也可以进行圆周运算。具体就是，你可以把有限长序列以它的长度为周期，进行周期延拓成一个周期序列，然后进行运算，然后取其主值区间进行观察得到的结果。

圆周反褶

圆周反褶就是一个周期序列进行反褶之后，取其主值区间序列。因为一个周期序列反褶之后还是周期序列，所以这么做是合理的。

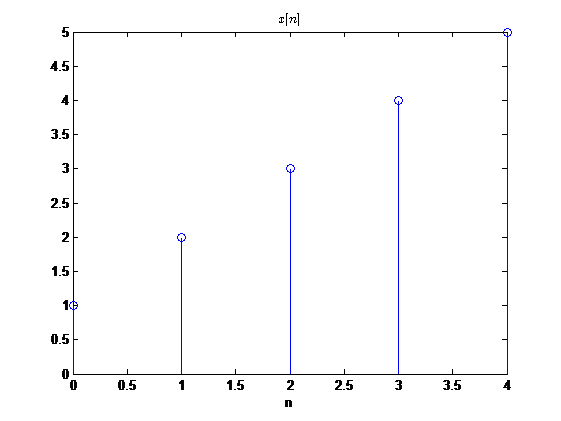
假设一周期信号在其主值区间的取值为$$x[n]={x[0],x[1],x[2],x[3],x[4]}$$即该序列的周期为$5$，那么反褶后的信号为(只关注主值区间)

\[\begin{aligned} y[0]&=x[0]=x[0] \\ y[1]&=x[-1]=x[5-1]=x[4] \\ y[2]&=x[-2]=x[5-2]=x[3] \\ y[3]&=x[-3]=x[5-3]=x[2] \\ y[4]&=x[-4]=x[5-4]=x[1] \end{aligned} \]

为了方便用数学的语言描述这种运算，首先看一种数学上的模运算运算，首先看几个模运算的例子：

\[\begin{aligned} 2 \,mod \, 5 =2 \\ 6 \, mod \, 5 = 1 \\ -3 \, mod \, 5 = 2 \end{aligned} \]

不知道大家看出来没有，模运算其实就是求余，$2$对$5$的余数就是$2$，$6$对于$5$的余数是$1$，而$-3$对$5$的余数应该为$(-3+5)\, mod\, 5=2$(加上$5$之后不影响余数的大小，因为$5$一直能整除$5$，$5$对$5$的余数一直是$0$)

我们把$2 \, mod\, 5$记作$<2>_5$，所以我们定义圆周反褶为

\[y[n]=x[<-n>_N] \]

其中$N$为序列$x[n]$的长度。

由上面的公式可以看出，与一般的反褶不同的是，序列下标经过了一次模运算。并且经过上面的数学化的定以后，圆周运算就不仅仅只对周期信号有效了，对一般的有限长信号都是有效的。

用计算画图看一下进行圆周反褶后的效果：

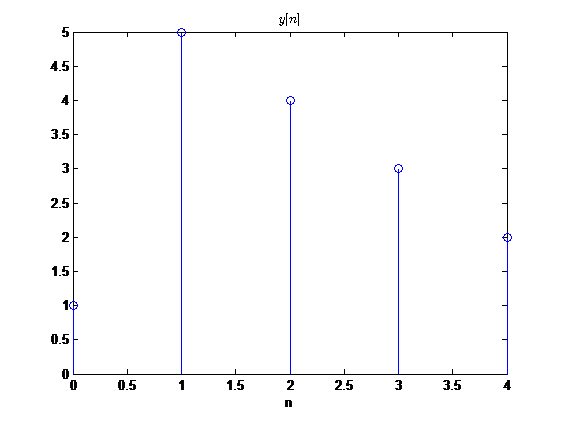
而一般的反褶又是什么样子的呢？还是通过计算机画图观察：

看到这里二者发现不仅波形不一样，并且有值区间也不一样，一般反褶的有值区间变为了$-4 \leq n \leq 0$，而圆周反褶的有值区间是$0 \leq n \leq 4$。

这个例子给出的就是有限长序列的圆周反褶运算，圆周运算是从周期序列扩展而来的，但不仅仅只针对于周期序列。事实上，后面的处理的圆周运算大部分都是有限长的序列。

圆周时移

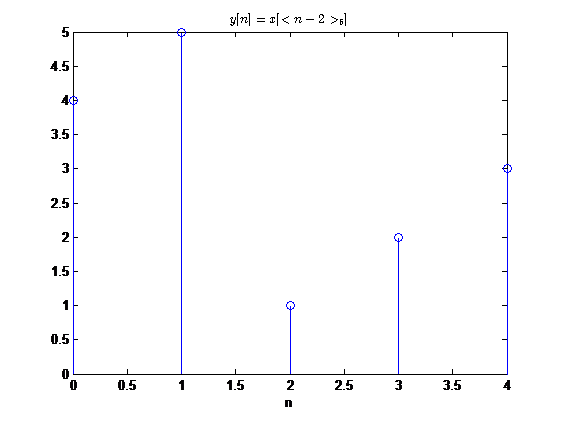
由圆周反褶的概念，不难定义出圆周时移，即：

\[y[n]=x[<n-n_0>_N] \]

与圆周反褶类似，$y[n]$的有值区间还是与$x[n]$相同。

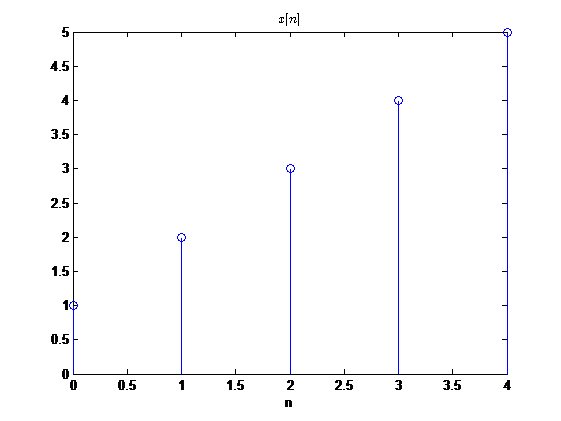
我们来直观的感受一下，圆周时移到底是怎么一个效果：

这完全可以看做是将序列进行周期延拓之后，然后进行时移，取其主值区间进行观察得到的结果。

圆周卷积

设两周期信号$\tilde{x}[n],\tilde{w}[n]$的周期都为$N$，它们的线性卷积为

\[\tilde{y}[n]=\sum_{m=-\infty}^{\infty}\tilde{x}[m]\tilde{w}[n-m] \]

易知序列$\tilde{y}[n]$也为周期序列，其周期为$N$。

设序列$\tilde{y}[n]$的主值区间为$y[n]$,$\tilde{y}[n]$的$DFS$为$\tilde{Y}[k]$,$y[n]$的$DFT$为$Y[k]$,由$DFS$与$DFT$的关系，得到$Y[k]$为$\tilde{Y}[k]$的主值区间。

\[\tilde{Y}[k]=\tilde{X}[k]\tilde{W}[k] \]

$\tilde{X}[k]$为序列$\tilde{x}[n]$的$DFS$,$\tilde{W}[k]$为序列$\tilde{w}[n]$的$DFS$,所以得到

\[Y[k]=X[k]W[k], \, 0 \leq k \leq N-1 \]

则

\[\begin{aligned} y[n]&=\frac{1}{N}\sum_{k=0}^{N-1}Y[k]e^{j\frac{2\pi kn}{N}} \\ &=\frac{1}{N}\sum_{k=0}^{N-1}X[k]W[k]e^{j\frac{2\pi kn}{N}} \\ &=\frac{1}{N}\sum_{k=0}^{N-1}\sum_{m=0}^{N-1}x[m]e^{-j\frac{2\pi km}{N}}W[k]e^{j\frac{2\pi kn}{N}} \\ &=\sum_{m=0}^{N-1}x[m](\frac{1}{N}\sum_{k=0}^{N-1}W[k]e^{j\frac{2\pi k(n-m)}{N}}) \\ &=\sum_{m=0}^{N-1}x[m]w[<n-m>_N] \end{aligned} \]

所以定义有限长序列的圆周卷积为

\[\color{red}y[n]=\sum_{m=0}^{N-1}x[m]w[<n-m>_N]=x[n]\text{\textcircled N}w[n] \]

其中序列$x[n]$和序列$w[n]$的长度都为$N$,易知卷积后的序列$y[n]$的长度也为$N$。

圆周卷积与线性卷积的关系

考虑两有限长序列$x[n]$和$w[n]$,$x[n]$的有值区间为$0\backsim N_1-1$,即其长度为$N_1$,$w[n]$的有值区间为$0\backsim N_2-1$,其长度为$N_2$,记其线性卷积为$y[n]$,则

\[y[n]=\sum_{m=-\infty}^{\infty}x[m]w[n-m]=\sum_{m=0}^{N_1-1}x[m]w[n-m] \]

其长度为$M=N_1+N_2-1$

为了求其圆周卷积$y_{L}[n]$，将$x[n]$和$w[n]$补零延拓为长度为$L$的序列，其中$L\geq max\{N_1,N_2\}$，则

\[\begin{aligned} y_L[n]&=\sum_{m=0}^{L-1}x[m]w[<n-m>_L], \, 0 \leq n \leq L-1\\ &=\sum_{m=0}^{L-1}x[m]\tilde{w}[n-m], \, 0 \leq n \leq L-1 \\ &=\sum_{m=0}^{L-1}x[m]\sum_{k=-\infty}^{\infty}w[n-m-kL], \, 0 \leq n \leq L-1 \\ &=\sum_{k=-\infty}^{\infty}\sum_{m=0}^{L-1}x[m]w[n-kL-m], \, 0 \leq n \leq L-1 \\ &=\sum_{k=-\infty}^{\infty}y[n-kL], \, 0 \leq n \leq L-1 \end{aligned} \]

所以L点圆周卷积是其线性卷积以周期为L进行周期延拓得到的结果。

由上图(这里不好画离散的图，用连续的表示一下，原理是一样的)知，当$L>N_1+N_2-2=M-1$时，即$L\geq M$时，即序列补零扩展后的长度大于线性卷积后的长度时

\[\sum_{k=-\infty}^{\infty}y[n-kL] \]

未发生混叠，取其主区间即是圆周卷积$y_L[n]$,取圆周卷积$y_L[n]$的前$N_1+N_2-1$个点就是线性卷积$y[n]$的值。

但是当$L < M$时

\[\sum_{k=-\infty}^{\infty}y[n-kL] \]

发生了混叠，如下图

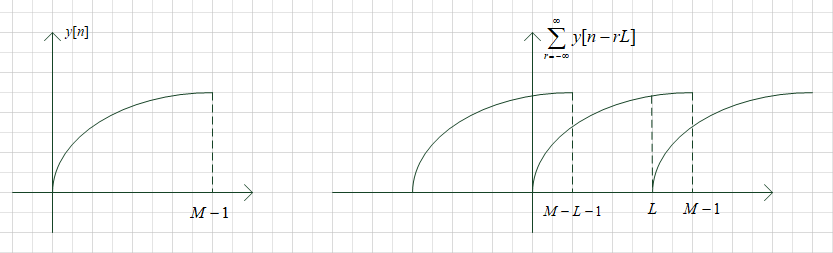
由图可知，只有$M-L \backsim L-1$这$2L-M$个点未发生混叠。所以如果补零扩展得到的长度$L<M$的话，那么得到圆周卷积$y_L[n]$中，只有在$M-L \backsim L-1$的取值与线性卷积的取值相同。

所以用圆周卷积计算有限长序列线性卷积的方法为:

将序列$x[n],w[n]$进行补零延拓，延拓后的长度$L$应大于等于卷积后的长度$M$
将补零延拓得到的序列进行圆周卷积运算
取圆周卷积的前$M$个即为线性卷积的结果

posted on 2019-05-31 23:35 LastKnight 阅读(1492) 评论(0) 编辑收藏举报