【机器学习】名词解释-神经元、前向传播、反向传播、损失函数

1. 单个神经元：

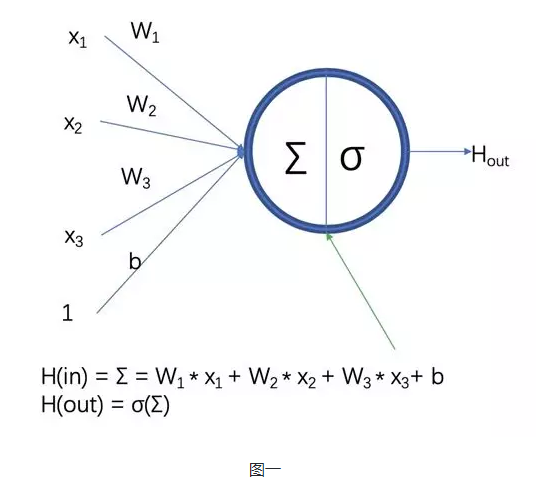
Y为输出结果，x为输入，w为权重，b为偏置

 

训练神经网络，其实就是不断地调整w和b的值，使之得到一个合适的值，最终这个值配合运算公式形成的逻辑，此为神经网络的模型

2. 前向传播：

不同的神经网络结构前向传播的方式是不一样的，最简单的前向传播算法即上面公式，输入x经过权重w和偏置b得到结果y

3. 反向传播

网络训练前，我们并不知道w和b是多少，反向传播的作用就是根据前向传播得到的结果和实际的误差，反馈给网络，网络根据误差来调整权重得到最优值

4. 损失函数

这在（反向传播）中说的用于描述模型结果与实际值误差大小

常用的损失函数有均方误差（MSE）和交叉熵

1. 均方误差/均值误差

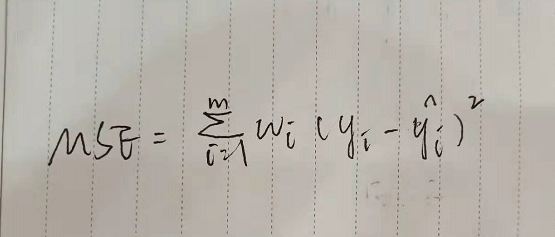
i样本个数      y真实值         y^预测

 

注：

在tensorflow中:

mse=tf.reduce_mean(tf.square(y_-y))

2. 交叉熵（多分类）

用于度量两个概率分布间的差异信息，使用损失函数（误差）来让交叉熵不断趋于最小（最优）

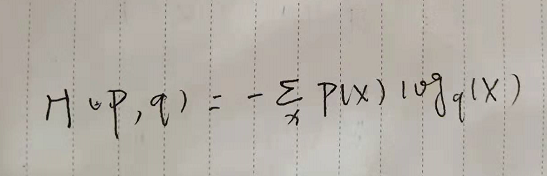
注：

在tensorflow中：

       cross_entropy= -tf.reduce_sum(labels*tf.log(logits))

       或

       cross_entropy=tf,nn.softmax_cross_entropy_with_logits(logits,labels)

 

 

 

三分类实例讲解交叉熵

 

       某个样本的正确答案（p）是[1,0,0]

       某模型经过softmax激活后的答案即预测值（q）是[0.5,0.4,0.1]，那么它们的交叉熵为：

 

 

 

附注：

       分类问题：

              分类问题希望解决的是将不同样本分到事先定义好的类别中，如“是否合格”为二分类，(0-9)手写数字识别为十分类

       回归问题：

              回归问题解决的是具体数值的预测，如房价预测、销量预测，这些问题所需要预测的不是一个事先定义好的类别而是任意实数，解决回归问题一般只有一个输出节点，节点的输出值即预测值