ARIMA(p,d,q)模型
使用自习室的人流量由于课程需要，往往会呈现一种季节周期性的规律。而ARIMA(p,d,q)时间序列模型的最大优势在于对季节周期性数据指标的准确预测，十分符合我们的设计需求。但由于时间关系，我们仅对ARIMA时间序列模型进行了初步理论研究。
时间序列预测是以时间序列自身的连续性为基础，假设在基本大环境不变的情况下，通过挖掘历史数据之间的发展过程及规律性，进而对发展趋势做出估计，预测未来的一种方式。在进行时间序列分析的过程中，会选取不同分析方法针对事件特征和规律进行建模分析，尽可能的提高预测准确度和有效性。
而ARIMA(p,d,q)时间序列模型主要由自回归AR(p)模型和移动平均MA(q)模型结合演变而成。并结合了两种模型的特点：
（1）AR(P)自回归模型是对时间序列的自回归处理，仅通过时间序列变量的自身历史观测值来反映有关因素对预测目标的影响和作用。AR(p)模型的定义见下：
由定义可知，不考虑间接的相关数据，yt的值与其间隔超过p个的序列值将没有相关性。
（2）MA(q)移动平均模型是通过时间序列平均历史预测误差的集合建立而成，在上一组预测数据加上对应的预测误差从而得出当前预测数据和预测集合。MA(q)模型的定义见下：
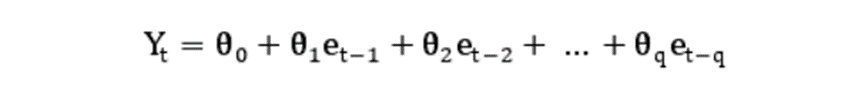
由定义可知，MA(q)模型的结果是序列et的q+1个单位近期数据的线性组合。因此et只会影响q+1的yt序列值，时间间隔超过q+1的两个et之间不存在任何联系。
根据以上定义可得ARIMA(p,d,q)模型的一般形式:
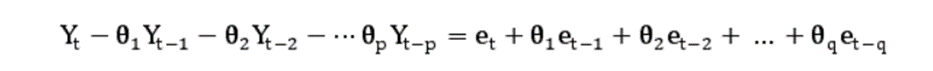
等式左边为模型的自回归部分，p为自回归阶数，{θ1,θ2,…,θp}为自回归系数；等式右边为模型的移动平均部分，q为移动平均阶数，{θ1,θ2,…,θq}为移动平均系数。
又由于ARIMA(p,d,q)模型只适用于平稳序列的分析，当实际情况下的时间序列并非平稳序列时，需对其平稳化，参数d即为平稳化过程需要差分的阶数。
时间序列分析
时间序列分析步骤：
1.载入历史数据，编成时间序列，并根据时间序列绘成统计图
2.分析统计图中的各种趋势、周期\季节性或随机行为。因为无法确定序列是否为平稳序列，要先对序列进行检验。可以使用目视检验，也可以使用一些统计方法如单位根平稳检验：ADF检验或KPSS检验。
单位根平稳检验：
设有一个时间序列:
其中yt是t时刻的数据值，εt是误差项，需要利用yt-1的值来计算yt，即
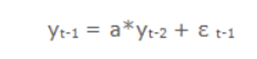
如果利用所有观察值，yt的值将是：
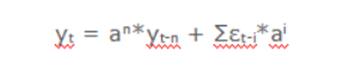
假设在上述方程中a的值为1（单位），则预测值将等于yt-n从t-n到t的所有误差之和，意味着方差将随着时间的推移而增大，这就是时间序列中的单位根。而平稳时间序列的方差不能是时间的函数，因此单位根检验通过检查a=1的值来检查序列中是否存在单位根。
ADF检验：
原假设：序列有一个单位根(a=1的值) 备译假设：该序列没有单位根
如ADF检验的检验统计量为1%，p值为5%，临界值为10%，置信区间为10%。如果检验统计量小于临界值，我们可以拒绝原假设，即序列是平稳的。反之则不
能拒绝原假设。
KPSS检验：
原假设：序列是趋势平稳的
备译假设：序列有一个单位根（序列式非平稳的）
如KPSS检验的检验统计量为1%，p值为2.5%，临界值为5%，置信区间为10%。当检验统计量大于临界值，则拒绝原假设（序列不是平稳的）。反之则不能拒绝原假设。
在为时间序列数据集准备模型之前，通常会同时进行两种检验，有可能两种检验得出结果不同：
结果1：均得出结论：序列是非平稳的->序列是非平稳的
结果2：均得出结论：序列是平稳的->序列是平稳的
结果3：KPSS=平稳；ADF=非平稳->趋势平稳，去除趋势后序列严格平稳
结果4：KPSS=非平稳；ADF=平稳->差分平稳，利用差分可使序列平稳
3.对非平稳序列进行平稳化。通常使用如下几种技术平稳化时间序列。
l 消除趋势：简单删除时间序列中的趋势成分。如，实现序列方程为
y(t) = (mean + trend * t) + error
简单删除公式中trend*t部分，建立y(t)=mean+error模型。
l 差分：在该中方法中，计算序列中连续项的差值。执行差分的操作通常是为了消除均值的变化。从数学角度，差分可写成：
yt‘ = yt – y(t-1)
l 季节性差分：
不计算连续值之间的差异，而是计算观察值与同一季节的先前观察值之间的差异，从数学角度可写成：
yt‘ = yt – y(t-n)
l 变换：变换用于对方差为非常数的序列进行平稳化。常用的变换方法包括幂变换、平方根变换和对数变换。
ARIMA(p,d,q)模型中的参数d即为平稳化过程需要差分的阶数。
4.分析ACF、PACF图得到最佳阶层p和最佳阶数q
根据图中拖尾和截尾情况得到参数p、q：
拖尾：序列以指数率单调递减或震荡衰减。 截尾：序列从某个时点变得非常小。
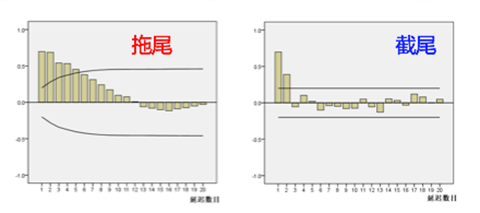
如以下情况通常视为(偏)自相关系数拖尾: 如以下情况通常视为(偏)自相关系数d阶截尾：
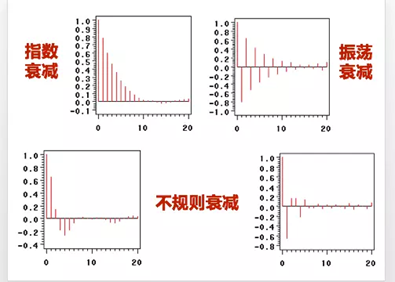
参数p、q的 确定：
自相关函数ACF描述的是时间序列观察值与其过去观察值之间的线性相关性。偏自相关函数PACF则描述在给定中间预测值的条件下，时间序列观测值与其过去观测值之间的线性相关性。
例如：k=3，描述的是yt和yt-3之间的相关性，但此相关性还受到yt-1、yt-2的影响。PACF剔除了此影响而ACF包含此影响。
5.可用ARIMA()p,d,q模型进行预测得到时间序列预测值。
附草稿笔记：
