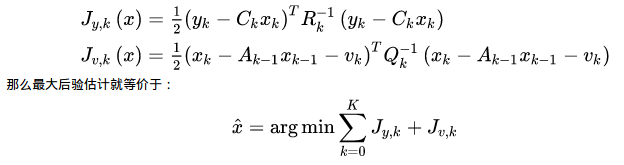kalman滤波（三）---各种滤波的方法汇总+优化的方法

大神解答

一.前提

       最一般的状态估计问题，我们会根据系统是否线性，把它们分为线性/非线性系统。同时，对于噪声，根据它们是否为高斯分布，分为高斯/非高斯噪声系统。现实中最常见的，也是最困难的问题，是非线性-非高斯(NLNG, Nonlinear-Non Gaussian)的状态估计。下面先说最简单的情况：线性高斯系统。

线性高斯系统

在线性高斯系统中，运动方程、观测方程是线性的，且两个噪声项服从零均值的高斯分布。这是最简单的情况。简单在哪里呢？主要是因为高斯分布经过线性变换之后仍为高斯分布。而对于一个高斯分布，只要计算出它的一阶和二阶矩，就可以描述它（高斯分布只有两个参数）。
　　线性系统形式如下：
　　其中是两个噪声项的协方差矩阵；为转移矩阵和观测矩阵；表示的后验概率，用表示它的先验概率。因为系统是线性的，噪声是高斯的，所以状态也服从高斯分布，需要计算它的均值和协方差矩阵。记第时刻的状态服从：
　　对LG系统，可以用贝叶斯法则，计算的后验概率分布——这条路直接通向卡尔曼滤波器。卡尔曼是线性系统的递推形式（recursive，也就是从估计）的无偏最优估计。

    （其中过程可以参考贝叶斯法则-最大似然估计）

     现在的问题是如何求解这个最大化问题。对于高斯分布，最大化问题可以变成最小化它的负对数。当我对一个高斯分布取负对数时，它的指数项变成了一个二次项，而前面的因子则变为一个无关的常数项，可以略掉（这部分我不敲了，有疑问的同学可以问）。于是，定义以下形式的最小化函数：

     写成矩阵的形式，类似最小二乘的问题：

　　于是令它的导数为零，得到：
 
　　读者会问，这个问题和卡尔曼滤波有什么问题呢？事实上，卡尔曼滤波就是递推地求解上式的过程。所谓递推，就是只用来计算。对(*)进行Cholesky分解，就可以推出卡尔曼滤波器。只把卡尔曼的结论写一下：

另一方面，能否直接求解(*)式，得到呢？答案是可以的，而且这就是优化方法（batch optimization）：将所有的状态放在一个向量里，进行求解。与卡尔曼滤波不同的是，在估计前面时刻的状态（如）时，会用到后面时刻的信息（等）。从这点来说，优化方法和卡尔曼处理信息的方式是相当不同的。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

二.扩展卡尔曼滤波器 --- EKF自己总结（针对非线性非高斯系统）

滤波器自己的局限性:

1. 即使是高斯分布，经过一个非线性变换后也不是高斯分布。EKF只计算均值与协方差，是在用高斯近似这个非线性变换后的结果。（实际中这个近似可能很差）。
2. 系统本身线性化过程中，丢掉了高阶项。
3. 线性化的工作点往往不是输入状态真实的均值，而是一个估计的均值。于是，在这个工作点下计算的，也不是最好的。
4. 在估计非线性输出的均值时，EKF算的是的形式。这个结果几乎不会是输出分布的真正期望值。协方差也是同理。

那么，怎么克服以上的缺点呢？途径很多，主要看我们想不想维持EKF的假设。如果我们比较乖，希望维持高斯分布假设，可以这样子改：

1. 为了克服第3条工作点的问题，我们以EKF估计的结果为工作点，重新计算一遍EKF，直到这个工作点变化够小，为迭代EKF（Iterated EKF, IEKF）。
2. 为了克服第4条，我们除了计算，再计算其他几个精心挑选的采样点，然后用这几个点估计输出的高斯分布。是为Sigma Point KF（SPKF，或UKF）。

如果不那么乖，可以说：我们不要高斯分布假设，凭什么要用高斯去近似一个长得根本不高斯的分布呢？于是问题变为，丢掉高斯假设后，怎么描述输出函数的分布就成了一个问题。一种比较暴力的方式是：用足够多的采样点，来表达输出的分布。这种蒙特卡洛的方式，也就是粒子滤波（PF）的思路。
　　如果再进一步，可以丢弃滤波器思路，说：为什么要用前一个时刻的值来估计下一个时刻呢？我们可以把所有状态看成变量，把运动方程和观测方程看成变量间的约束，构造误差函数，然后最小化这个误差的二次型。这样就会得到非线性优化的方法，在SLAM里就走向图优化那条路上去了。不过，非线性优化也需要对误差函数不断地求梯度，并根据梯度方向迭代，因而局部线性化是不可避免的。
　　可以看到，在这个过程中，我们逐渐放宽了假设。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

三.IEKF

四.UKF无迹卡尔曼滤波

五. PF 粒子滤波

六. CKF 容积卡尔曼滤波

七. 非线性优化

非线性优化，计算的也是最大后验概率估计（MAP），但它的处理方式与滤波器不同。对于上面写的状态估计问题，可以简单地构造误差项：
　　然后最小化这些误差项的二次型：
       这里仅用到了噪声项满足高斯分布的假设，再没有更多的了。当构建一个非线性优化问题之后，就可以从一个初始值出发，计算梯度（或二阶梯度），优化这个目标函数。常见的梯度下降策略有牛顿法、高斯-牛顿法、Levenberg-Marquardt方法。
　　非线性优化方法现在已经成为视觉SLAM里的主流，尤其是在它的稀疏性质被人发现且利用起来之后。它与滤波器最大不同点在于， 一次可以考虑整条轨迹中的约束。它的线性化，即雅可比矩阵的计算，也是相对于整条轨迹的。相比之下，滤波器还是停留在马尔可夫的假设之下，只用上一次估计的状态计算当前的状态。可以用一个图来表达它们之间的关系：
　　当然优化方式也存在它的问题。例如优化时间会随着节点数量增长——所以有人会提double window optimization这样的方式，以及可能落入局部极小。但是就目前而言，它比EKF还是优不少的。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 总结

1. 卡尔曼滤波是递归的线性高斯系统最优估计。
2. EKF将NLNG系统在工作点附近近似为LG进行处理。
3. IEKF对工作点进行迭代。
4. UKF没有线性化近似，而是把sigma point（采样点）进行非线性变换后再用高斯近似。
5. PF去掉高斯假设，以粒子作为采样点来描述分布。
6. 优化方式同时考虑所有帧间约束，迭代线性化求解。

 

PS：

　　SLAM中，状态变量经常是六自由度的位姿，由旋转矩阵和平移向量构成。然而问题是，旋转矩阵并不存在加法，只有对应到李代数上才可以清楚地定义它的运算。因此，当我们讨论这个位姿的噪声，说它服从高斯分布时，需要了解李群李代数的知识。