PL-SVO是基于点、线特征的半直接法单目视觉里程计，我们先来介绍一下基于点特征的SVO，因为是在这个基础上提出的。
[1]References： SVO: Fast Semi-Direct Monocular Visual Odometry
---Christian Forster, Matia Pizzoli, Davide Scaramuzza ∗
从名字来看，是半直接视觉里程计，所谓半直接是指通过对图像中的特征点图像块进行直接匹配来获取相机位姿，而不像直接匹配法那样对整个图像使用直接匹配。整幅图像的直接匹配法常见于RGBD传感器，因为RGBD传感器能获取整幅图像的深度。 虽然semi-direct方法使用了特征，但它的思路主要还是通过direct method来获取位姿，这和feature-method不一样。同时，semi-direct方法和direct method不同的是它利用特征块的配准来对direct method估计的位姿进行优化。
总结：半直接法（特征点法与直接法混用），跟踪一些关键点（没有描述子），然后像直接法那样根据这些关键点周围的信息（4×4的图像块）匹配来估计相机的位姿.
注意：1. 在1.sparse model-based image alignment 2.Relaxation Through Feature Alignment 中使用的都是光度误差（像素差异），在3.Pose and Structure Refinement 中是优化后的特征位置和之前预测的特征位置存在的差异。
可以详细看SVO的wiki，很有用：https://github.com/uzh-rpg/rpg_svo/wiki
rpg_svo/svo/doc：
Notation
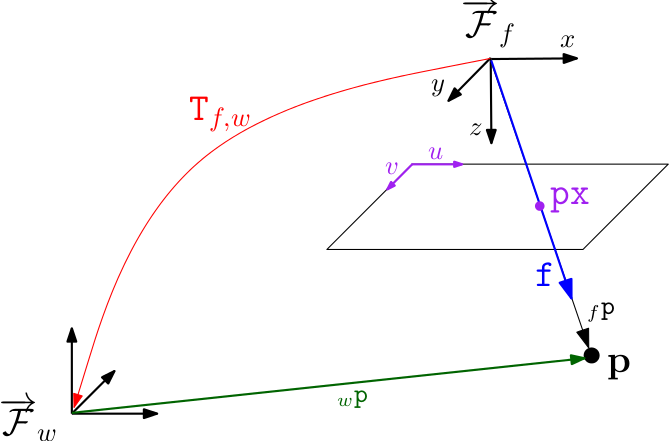
px - Pixel coordinate (u,v)
f - Bearing vector of unit length (x,y,z)
T_f_w - Rigid body transformation from world frame w to camera frame f.
This transformation transforms a point in world coordinates p_w to a point in frame coordinates p_f as follows: p_f = T_f_w * p_w.
The camera position in world coordinates must be obtained by inversion: pos = T_f_w.inverse().translation()
感谢这些好的博客
白巧克力：
路游侠：
http://www.cnblogs.com/luyb/p/5773691.html
冯兵：
可爱的小蚂蚁：
[2]Reference： PL-SVO: Semi-Direct Monocular Visual Odometry by Combining Points and Line Segments
---Ruben Gomez-Ojeda, Jesus Briales, and Javier Gonzalez-Jimenez
I. Introduction
在机器人应用中视觉里程计（VO）越来越重要，如无人机（UAV）或自主车，它作为导航系统的重要组成部分。为解决VO的问题已尝试采用不同的传感器，如单眼或立体摄像机[ 2 ] [ 3 ] [ 4 ]，RGB-D摄像机[ 5 ] [ 6 ]，或将其中的任何结合惯性测量单元（IMU）[ 7 ]。传统的方法包括检测和匹配帧间的特征点，然后，通过观测值和投影点[ 8 ]之间的重投影误差的最小二乘最小化来估计摄像机运动。在这种情况下，这种方法的性能在图1所示的低纹理场景中变坏，在那里很难找到一个大的或分布良好的图像特征集。与此相反，线段通常是丰富的在人工场景，其特点是丰富的边缘规则结构和线性形状。图像中处理的线段，它不像点那么简单，因为它们很难表示[ 9 ]，而且对检测和匹配任务也要求很高的计算量，因此只有少数的解决方案被提出[ 10 ] [ 11 ]，勉强达到实时性规范。此外，基于边缘的算法也被用于解决跟踪问题[ 12 ] [ 13 ] [ 14 ]，并估计相机运动[ 15 ]。然而，这些方法需要一个相当代价高的直接对准，这使得它们不太适合实时，也限制了其在狭窄的基线估计的应用。据我们所知，本文提出了的结合点和直线段特征的单目视觉里程计（MVO）的第一个实时方法，因此它能够有力地在结构和粗糙纹理的情况下工作源代码开发的C++ pl-svo库，这个提议的说明视频可以在这里找到：http://mapir.isa.uma.es
A. Related Work
视觉里程计算法可以分为两个主要群体。一个被称为基于特征的，提取一组图像特征（关键点）并沿着连续帧跟踪它们。然后，通过最小化观测到的特征点在不同帧中的投影之间的投影误差（最小化重投影误差）来估计姿态。文献为我们提供了一些基于点方法的测距问题，如PTAM[ 16 ]，其介绍了一种快速SLAM系统能够对成千上万个地标进行实时并行跟踪和映射。相比之下，线特征的运动估计问题较少探讨，由于其内在的困难，特别是在单目测距。在[17 ]中，作者将迭代最近点（ICP）方法[ 18 ]推广到具有线段的立体测距的情况下，在一对多的线匹配方法中他们替代代价高的描述符的计算。在我们以前的工作[ 19 ]，我们提出了一种基于点和直线段特征的立体视觉里程计系统{即PL-StVO}。每个特征的影响用它们的协方差矩阵的逆来加权来表示，它是通过重投影的不确定性传播技术获得。然而，这项工作仍然依赖于传统的特征检测和匹配，因此它具有很高的计算成本。
另一个被称为直接方法，通过最小化在多个图像位置上连续帧之间的光度误差来估计相机运动。在[ 20 ]提出了一种直接的方法，称为DTAM，他们估计相机的姿势通过直接对准在每个关键帧的完整的强度图[是表示单通道图像像素的强度（值的大小），即灰度图]，采用稠密深度图估计。然而，这种方法需要GPU并行处理，因为它处理整个图像。针对直接法的高计算要求，在[21]中提出了一种新的单目技术，在该方法中，作者用半密集的方法估计摄像机的运动，从而在CPU上达到实时性能。他们不断估计和跟踪一个具有足够图像梯度区域的半稠密逆深度图，因此仅利用那些将有效信息引入系统的区域。然后，他们通过最小化感兴趣区域上的光度误差来估计相机运动，从而将直接算法的良好性质与允许快速处理的稀疏方法相结合。
B. Contributions贡献
在低纹理和结构化的情景中点特征不丰富，因此，基于点的视觉里程算法的鲁棒性和准确性大大降低了。另一方面，检测和直线段匹配要求高的计算资源，这是对于通过这些特征进行视觉测距缺乏实时的主要原因。在这项工作中，我们将[ 1 ]的半直接方法扩展到了线段的情况，作为稀疏直接运动估计的隐式结果进行快速特征跟踪。因此，我们利用稀疏结构的这种优点，消除高代价的检测（当一个新的关键帧被引入到框架时，我们只进行稀疏检测）和描述符的计算，同时保持线段的良好性能。因此，我们提供快速的单目测距系统可工作在低纹理场景得益于点和线段特征的组合信息。接下来，我们描述了所提出的系统，并在不同的环境中通过实验验证了其优良的特性。
II. System Overview
所提出的系统可以理解为[ 1 ]中的半直接框架的扩展，它不仅考虑点，而且还包括场景中的线段特征，并在传递中引入这两个方面。这是一个不容易实现的扩展，因为线段从几何角度来看比点特征更复杂。在实践中，某些图像操作对于点是很方便的，但在线段的情况下变得十分繁琐。因此，为了节省计算资源，我们需要执行几个近似，并采取一些有根据的启发式方法。这些将在第III节和第IV节中详细介绍。
为了完整起见，我们简要回顾了[1]中半直接框架所示的每一阶段，如图2所示，同时展示了这种半直接方法和使用线段特性的融合如何变得互惠互利。半直接法分为两个平行线程，一个用于估计相机运动（定位），另一个用于映射环境（建图）。
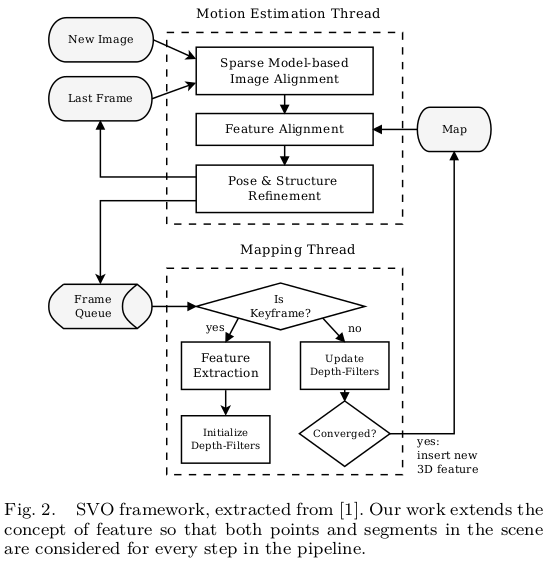
运动线程第一步，使用稀疏直接法在连续帧之间执行初始运动估计（图3）。该方法通过最小化图像块重投影误差（光度误差）来获取位姿。（这使得半直接运动估计的帧间特征的快速跟踪成为可能，消除了帧对帧检测和匹配的需要。这不仅对于点特征是相当有利的，而且对于线段来说也很有利，因为线段在计算上耗时更多。）特征从当一个新的关键帧插入中提取，使LSD线段检测[ 22 ]的总成本减小。此外，为了将姿态估计优化问题的维数降低，只需完成对极几何的自动执行，不必考虑异常匹配。
运动线程的第二步，对由直接对齐变换估计给出的特征投影进行优化（图4），从而违反极线约束以减少相机的漂移。特征优化是以最接近的视点作为参考块进行的。并且这种方法对线段非常有益，因为它在跟踪线段时限制了较大的观测基线。因此，它减轻了众所周知的线段的问题，例如端点的重复性、遮挡或由于视图的改变而引起的线段形变[ 11 ]。
运动线程的第三步，相机的位姿和结构图（三维点）是通过最小化重投影误差改善的（图5）。
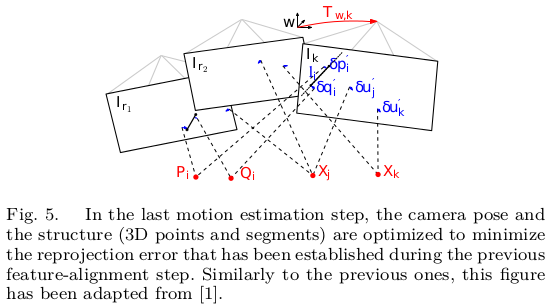
此时，由于中间连续跟踪，远特征的匹配得到了充分的解决，并且我们可以应用特定的基于特征的优化方法，这些方法可以很好地处理线段特征。
综上所述，我们看到，在一个半直接框架[ 1 ]中线段的引入，对于其他更传统的方法，可以做到更好的实现，从初步的直接步骤缓解大多数历来在视觉里程计阻止线段使用的缺点。另外，运动和映射线程通过线段的使用而变得丰富，而不会引起整个系统的很大消耗。
地图线程估计2D特征的深度有个概率贝叶斯过滤器，每当新的关键帧插入，对其进行特征提取得到种子点，初始化深度滤波器，并用普通帧来更新深度滤波器，多次观测到它的深度，并将其融合更新深度。深度滤波器初始化时具有很高的不确定性，但它们在几次迭代中收敛到实际值，然后插入到map中，对运动估计非常有用。
接下来，我们详细描述了算法的各个阶段，并在实际环境中进行了实验验证。
III. Semi-Direct Monocular Visual Odometry
和
是在标定的相机坐标系中两个连续的相机姿态，由相对位姿变换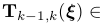
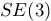关联起来，其中
是6-矢量（6×1）坐标，属于李代数
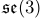。我们面临的问题是，在一个帧序列中估计相机的位姿，用
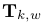表示为在世界坐标系中在第k时刻的相机姿态，
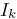表示为第k帧的灰度图像（intensity image）[指的是：单通道图像像素的强度（值的大小）,在灰度图像中intensity 指的就是图像的灰度]和Ω表示为图像域。我们将图像上点特征表示为
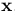，对应的深度为
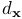。在线段的情况下，我们将采用两个端点，分别由p和q表示，和线方程为l表示。从图像反投影的3D点在时间k表示为
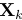，并可通过逆投影功能
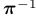获得，即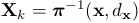
。在图像域的三维点的投影是通过相机投影模型
获得，也就是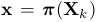
。在下面，我们将扩展SVO算法到线段的情况下。
A. Sparse Model-based Image Alignment（稀疏直接法，初始运动估计）
两连续帧之间的相机运动，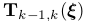
，首先通过稀疏特征沿帧跟踪直接图像对准估计。与基于点的方法不同，我们不能直接对齐两帧之间的线段所占据的整个区域，因为这在计算上代价高。为此，我们只最小化均匀分布在线段上部分图像块的图像误差，如图3所示。让我们定义L为端点的深度在以前的时刻k−1已知的图像区域，而终点p和q是在目前时刻
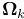在图像域可见：
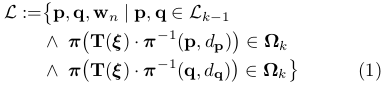
其中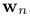 
，n = 2, ..., 
，指沿线段均匀定义的中间点。然后，线段的灰度误差（残差）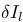
定义为相同3D线段点像素之间的光度差，如下：
当n=0和n=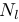
时，点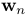
分别指端点p和q。
（将优化问题转成了最小二乘问题）我们估计最优姿态增量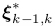
，最小化所有像素块的光度误差，对于点和线段特征：
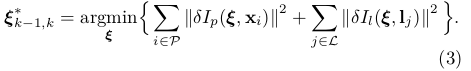
类似于[ 1 ]，我们在[ 23 ]中提出了加速最小化的逆合成公式。在这种情况下，我们寻找线段残差的线性雅可比矩阵，它可以表示为对于每个中间采样点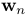的雅可比矩阵的总和：
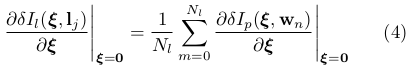
其表达式可由[ 1 ]获得。然后，我们估计最佳姿态通过鲁棒Gauss Newton最小化（3）式。注意，这个公式允许快速跟踪线段，如图1所示，这是一个有议论余地的问题，因为采用传统的基于特征的方法[ 19 ]所需的计算负担很高。
B. Individual Feature Alignment个体特征调整（优化）
通过第一步的帧间匹配能够得到当前帧相机的位姿，但是这种frame to frame估计位姿的方式不可避免的会带来累计误差从而导致漂移。所以，应该通过已经建立好的地图模型，来进一步约束当前帧的位姿。
类似于[ 1 ]，我们单独细化每个特征的2D位置，通过最小化该特征在当前图像中的图像块（真实值，蓝色方框块）和其观测3D特征的投影（估计值，灰色方框块）之间的光度误差，可采用Lucas Kanade算法[ 23 ]解决。在线段的情况下，我们只需要改进2D端点的位置（参见图4），它定义了投影误差估计中使用的直线方程：
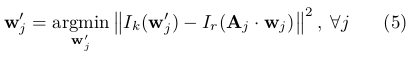
其中，
是当前帧中特征位置的二维估计（维持两个端点都相等 ），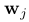
是特征在参考帧r中的位置。这是在线段的情况下一个大胆的假设，因为他们的端点比关键点相当少的描述。为了处理这个问题，我们还执行了一个鲁棒优化（5），然后通过改进端点的三维位置来放宽这个假设。注意，在这一步中使用仿射变形A是必要的，因为我们投射该特征的最接近的关键帧通常是远的，而且图像块的大小比先前的更大。
通过这一步我们能够得到优化后的特征点预测位置，它比之前通过相机位姿预测的位置更准，所以反过来，我们利用这个优化后的特征位置，能够进一步去优化相机位姿以及特征点的三维坐标。所以位姿估计的最后一步就是Pose and Structure Refinement。
C. Pose and Structure Refinement
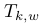，都在世界坐标系中，它大大降低了估计轨迹的漂移。当使用这两种类型的特征时，方程是：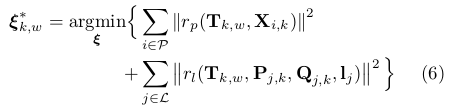
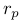代表点特征情况下的投影误差，
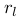代表线特征情况下的投影误差：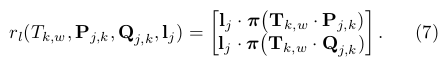
这是用Gauss Newton迭代求解，为此我们需要包括（6）在一个稳健的框架，并采用柯西损耗函数：
优化包括三个步骤：（i）首先估计所有样本的相机运动。（ii）我们筛选出异常数据，这些特征的残余误差是两倍以上的稳定标准差。（iii）我们快速细化相机姿态通过内点集的优化。最后，我们改进的三维点和线段特征的位置通过最小化投影误差。
IV. Mapping
V. Experimental Validation
在本节中，我们演示了在运动估计中包含线段的好处，特别是在低纹理环境下工作。为此，我们从模拟和真实数据中估计单目摄像机在多个序列中的轨迹。所有的实验已经进行了一个英特尔酷睿i5-6600CPU @ 3.30GHz没有GPU并行。
A. Evaluation in ICL-NUIM Dataset [25]
RMSE：均方根误差
Median:平均值
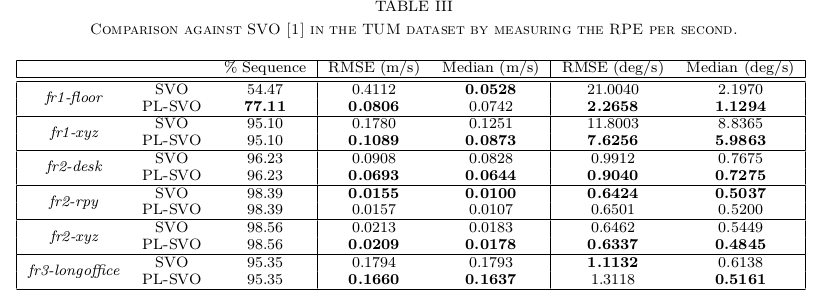
B. Evaluation in TUM Dataset [26]
C. Processing Time
SVO和pl-svo算法在每个算法阶段的平均时间：
Pyramid creation金字塔创造
Sparse Image Alignment 稀疏图像对齐
Feature Alignment 特征定位
Pose and Structure Refinement 位姿与结构细化
Total Motion Estimation 总运动估计
VI. Conclusions
References
[1] C. Forster, M. Pizzoli, and D. Scaramuzza, “SVO : Fast Semi-Direct Monocular Visual Odometry,” IEEE Interna-
tional Conference on Robotics and Automation, 2014.
[3]Reference： Robust Stereo Visual Odometry through a Probabilistic Combination of Points and Line Segments
---Ruben Gomez-Ojeda, Javier Gonzalez-Jimenez
Abstract---立体视觉测距的大多数方法基于沿着图像序列的点特征的跟踪来重建运动。然而，在低纹理的场景中，通常很难遇到大的点特征集合，或者可能发生的是它们在图像上分布不好，从而使得这些算法的行为恶化。本文提出了一种基于点和线段的组合的立体视觉测径的概率方法，该方法在各种场景中稳健地工作。通过非线性地最小化点和线段特征的投影误差来恢复相机运动。为了有效地结合这两种类型的特征，它们的相关误差根据它们的协方差矩阵来加权，根据在传感器测量中的高斯分布误差的传播来计算。当然，该方法相比于只使用一种类型的特征在计算上更昂贵，但仍然可以在计算机上实时运行并有很多优点，包括在移动机器人中普遍使用的任何概率框架中的直接集成。
I. Introduction
II. System Overview
简而言之，我们跟踪立体帧序列中的特征（点和片段）并计算它们的3D位置及其相关的不确定性。然后将3D地标投影到新的相机姿态，其中误差函数被最小化，以得到相机的姿态增量和该估计的不确定性。下面我们介绍SVO系统的每一个步骤，并描述其实现的最重要的细节。
1）点特征：为了处理特征点，我们采用ORB【14】检测器和描述符，因为它的效率和良好的性能。为了减少离群点的数量，我们只考虑相互最佳匹配的测量，即左图像中的最佳匹配对应于右图中的最佳匹配。为了确保对应关系是有意义的，我们还检查在两个最接近匹配之间的描述空间中的距离高于某个阈值，该距离被设置为最佳匹配距离的两倍。我们还确保了在输入图像上的点分布的公平性，并用一个ButkTein方法将图像分成16个 buckets，并尽量每个中至少有20个特征。
2）线段特征：线段检测器（LSD）【15】检测线段，具有较高的精度和可重复性。然而，耗时，这是其实时应用的主要弱点。为了减轻这一点，我们检测在两个立体图像中的并行化的框架中的线段。 对于立体匹配和帧到帧跟踪，我们首先计算每一行的LBD描述符【16】，并根据它们的局部外观特征来匹配它们。类似于点的情况，我们检查这两个特征是相互最佳匹配，并且最好的两个匹配在描述空间中被充分分离。我们还没有在线段检测中应用一种bucket策略，因为它提供了不太可靠的特征，会因此产生较差的结果。
3）运动估计：一旦特征从立体帧跟踪到下一帧，线段端点和特征点已经进行反投影。然后，通过线和点投影误差的概率高斯牛顿最小化迭代估计运动。不正确对应的负面影响通过采用Pseudo- Huber损失函数检测和去除异常值，如【17】中提出的。完整的过程将在第三节中详细说明。
4）不确定性传播：为了提高增量姿态估计的精度，我们用误差协方差矩阵的逆来加权它们。该协方差矩阵是通过传播假设为零均值高斯分布的特征误差（计算机视觉中的一个共同假设）来获得的。
最终，这种传播过程以估计姿态的不确定性结束，这使得我们的系统适合于容易地集成在任何概率机器人算法中。误差分布将在第四节中进行描述和验证。
