模拟退火
一:概括
1.爬山算法
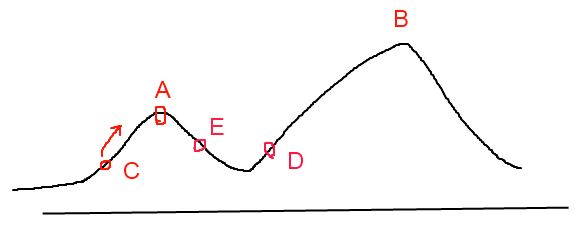
所谓的爬山算法实际上就是简单的贪心算法,贪心算法通过从当前解的临近空间选择一个最优的解作为新的当前解,因此这个解很有可能是局部最优解,而不是全局最优的。因为A的领域周围没有比他更优的解了。
2.模拟算法
模拟退火算法可以有效的解决这个陷入局部最优解的问题从而找到一个全局最优解。实际上模拟退火算法也是贪心算法,只不过它在这个基础上增加了随机因素。这个随机因素就是:以一定的概率来接受一个比单前解要差的解。通过这个随机因素使得算法有可能跳出这个局部最优解
二:起源
以爬山算法为代表的局部搜索算法仅仅适用于某类组合优化问题并且解的质量也不是很理想。于是为了克服这些缺点,人们通过一些自然物理过程寻找解决办法模拟退火算法源于对固体的退火过程的模拟,通过采用Metropolis接受准则,并用一组称为冷却表的参数控制算法进程,使得我们可以在多项式时间内求出一个近似最优解。
固体退火:
1.先将固体加热至溶化然后徐徐冷却。
2.退火要徐徐进行使得系统在每一温度下都达到平衡。
3.冷却时不能急剧减温。
模拟退火算法:
1、从某个初始解i0出发,经过L次解的变换(每次根据Metropoils算法求解),求得在给定温度下的相对最优解。
2、减小控制参数T,重新变换解(如上)
3、求得在控制参数T趋于0时的最优解
三:参数说明
1.Metropoils算法
这个算法是模拟退火的关键,其实也很好理解。前面说到,模拟退火之所以是可以找到全局近似最优解,是因为它在一定程度上接受某个差解,从而可以跳出局部最优解。那么它如何接受这个差解呢?就是靠这个Metropoils算法。
Metropoils其实就是定义了一个转移概率P:

当产生的新解比之前的效果好,那么我们以1的概率接受这个新解,用这个新解代替之前的解。如果这个新产生的解比之前的差,那么我们就以一定的概率接受它,这样我们就有可能跳出局部最优解。
2.Mapkob链长
其实呢,这个什么的链长其实很简单,但是它对算法的效果却很重要。我们提到,固体退火的时候要徐徐下降使得固定在该温度下达到平衡,那么对应到模拟退火来说其实就是在某个问题下得到一个稳定的最优解。如何得到这个稳定的最优解呢?很简单!不断迭代,不断产生新解然后采用 Metropoils准则接受这个新解,这样经过好多次好多次的迭代,就可以了。Mapkob链长就是迭代的次数啦。
3.温度T
这里温度T包括两个方面,一方面是初始温度,另一个就是温度的衰减问题。
初始温度:一般设置的大一点 ,T大一点可以保证初始阶段可以搜索到全局最优解的区域,如果太小就可能无法跳出局部解。设个100000什么的。
衰减函数:其实就是每次让温度如何下降的问题。T=ɑ*T. ɑ 一般取接近1的数,小一点的衰减量可以使得迭代次数增加,这样就可以产生更多变换解,就可以返回高质量的解。还可以有别的衰减函数。
四:实现
总结:算法在给定温度下持续进行“产生新解,计算目标函数,判断是否接受新解,接受或舍弃的迭代过 程”,然后降低温度,再进行上述过程。
1、初始化:设置参数(初始温度T、终止条件T<1,衰减函数T=a*T,Mapkob链长);
2、在给定温度下,不断产生新解并以Metropoils算法进行迭代Mapkob链长;
3、降低温度T,回到第二步;
4、结束;
效果:

我们可以看到不管采用哪个方法产生新解都会收敛到近似最优解。因此,模拟退火的求解能力还是很强的。
具体代码:https://github.com/guojiasheng/Tsp.git



