#luogu整理 P1967 货车运输

我好难过~ 这不是我要的那种~ 结果~ 结果~~~

luogu P1967 货车运输

我是从哪里学会的

\(crazydave\) 的题解

题目描述

$A $国有 \(n\) 座城市，编号从 \(1\)到\(n\)，城市之间有 \(m\)条双向道路。每一条道路对车辆都有重量限制，简称限重。

现在有 \(q\)辆货车在运输货物， 司机们想知道每辆车在不超过车辆限重的情况下，最多能运多重的货物。

输入

第一行有两个用一个空格隔开的整数 \(n, m\)，表示\(A\)国有\(n\)座城市和\(m\)条道路。
接下来\(m\)行每行三个整数\(x,y,z\)，每两个整数之间用一个空格隔开，表示从\(x\)号城市到\(y\)号城市有一条限重为\(z\)的道路。
注意: \(x≠y\)，两座城市之间可能有多条道路。
接下来一行有一个整数\(q\)，表示有\(q\)辆货车需要运货。
接下来\(q\)行，每行两个整数\(x, y\),之间用一个空格隔开，表示一辆货车需要从\(x\)城市运输货物到\(y\)城市，保证\(x≠y\)。

输出

共有 \(q\) 行，每行一个整数，表示对于每一辆货车，它的最大载重是多少。
如果货车不能到达目的地，输出 \(−1\)。

样例

\(in\)

4 3
1 2 4
2 3 3
3 1 1
3
1 3
1 4
1 3

\(out\)

3
-1
3

思路

最大生成树+LCA，这个题整体难度就在于代码的实现，因为这两种算法本身比较容易实现，可是放到一块，事情就没那么简单了。以下是程序实现。

首先建立两个图，一个图是输入的图，另一个是kruskal算法生成的图。我们要在第二个图上面进行倍增，所以后面的f[ ][ ]，v[ ][ ],dep[ ]数组记录的就是第二个图的倍增信息。另外，fa[ ]记录的是并查集的数组，表述的也是第二个图的并查集关系。

写代码时翻车出现在了LCA的掌握不准确，和两个图标识搞乱这两个问题上。

我的代码

（后面有debug的记录）

// 曹宇琮
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define INF 999999999
using namespace std;
int n,m;
int fa[6000000][30];
int v[6000000][30];
bool vis[6000000];
int dep[6000000];
struct EDGE{
    int from,to,v;
    int nxt;
}edge[100005],edgein[60006];
int cnt1 = 0,cnt2 = 0;
int head[6000000];
void add_tree_edge(int from,int to,int v){
    cnt2++;
    edge[cnt2].from = from;
    edge[cnt2].to = to;
    edge[cnt2].v = v;
    edge[cnt2].nxt = head[from];
    head[from] = cnt2;
}

int f[6000000];
int getfa(int x){
    return f[x] == x ? x : f[x] = getfa(f[x]);
}

bool cmp(EDGE x,EDGE y){
    return x.v > y.v;
}

void kruskal(){
    sort(edgein + 1 , edgein + 1 + m, cmp);
    for(int i = 1;i <= n; i++)
        f[i] = i;
    for(int i = 1;i <= m; i++){
        int x = edgein[i].from,y = edgein[i].to;
        if(getfa(x) != getfa(y)){
            f[getfa(x)] = getfa(y);
            add_tree_edge(x,y,edgein[i].v);
            add_tree_edge(y,x,edgein[i].v);//这里是最终错的地方（原来写的edge[i].v）
        }
    }
}

void dfs(int x){
    vis[x] = 1;
    for(int i = head[x];i;i = edge[i].nxt){
        if(!vis[edge[i].to]){
            int y = edge[i].to;
            fa[y][0] = x;
            dep[y] = dep[x] + 1;
            v[y][0] = edge[i].v;
            dfs(y);
        }
    }
}

int lca(int x,int y){
    if(getfa(x) != getfa(y))
        return -1;
    int ans = INF;
    if(dep[x] > dep[y]) swap(x,y);
    for(int i = 20;i >= 0; i--)
        if(dep[fa[y][i]] >= dep[x]){//①
            ans = min(ans,v[y][i]);
            y = fa[y][i];//②
        }
    if(x == y){return ans;}
    for(int i = 20;i >= 0; i--){
        if(fa[y][i] != fa[x][i]){
            ans = min(ans,min(v[y][i],v[x][i]));
            x = fa[x][i];
            y = fa[y][i];
        }
    }
    ans = min(ans,min(v[x][0],v[y][0]));
    return ans;
}

int main(){
    cin >> n >> m;
    for(int i = 1;i <= m; i++){
        int x,y,z;
        cin >> x >> y >> z;
        edgein[i].from = x;
        edgein[i].to = y;
        edgein[i].v = z;
    }
    kruskal();

    for(int i = 1;i <= n; i++){
        if(!vis[i]){
            dep[i] = 1;
            dfs(i);
            fa[i][0] = i;
            v[i][0] = INF;
        }
    }

    // for(int i = 0;i <= n; i++){
    //     for(int j = 0;j <= 20; j++){
    //         cout << v[i][j] << ' ';
    //     }
    //     cout << endl;
    // }

    for(int i = 1;i <= 20; i++){
        for(int j = 1;j <= n; j++){
            fa[j][i] = fa[fa[j][i-1]][i-1];
            v[j][i] = min(v[j][i-1],v[fa[j][i-1]][i-1]);
        }
    }

    int q;
    cin >> q;
    for(int i = 1;i <= q; i++){
        int x,y;
        cin >> x >> y;
        cout << lca(x,y) << endl;
    }
    return 0;
}

① 这里一开始写的是fa[y] >= dep[x]，没有考虑到我们用该看他移动以后位置如何

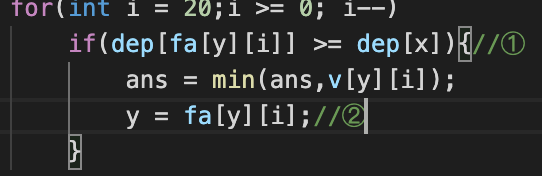
② 这里一开始把if里面的顺序写反了，记成了移动以后的v[y][i]值。

行吧这个题我调了好久才调出来。重新写一遍去。白白。