#QBXT2020寒假 Day 3下午
线段树
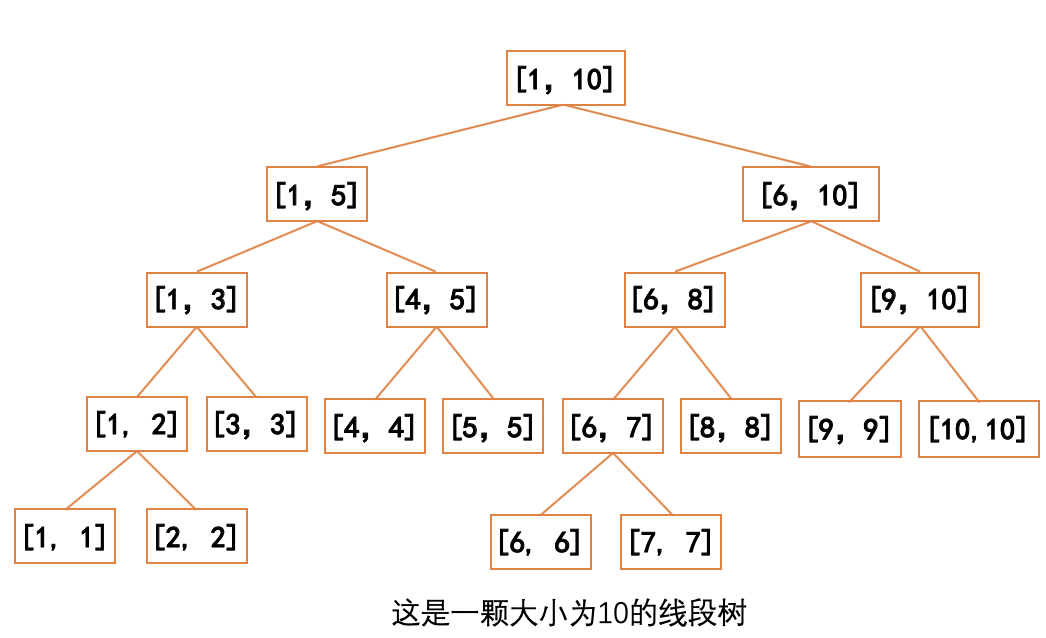
例题一 例题二
线段树模板
维护区间最小值个数
void pre(int rt){
t[rt].min = min(t[(ls(rt))].min,t[rs(rt)].min);
if(t[ls(rt)] > t[rs(rt)]){
t[rt].sum = t[ls(rt)];
}else if(t[ls(rt)] > t[rs(rt)]){
t[rt].sum = t[rs(rt)];
}else t[rt].sum = t[ls(rt)].sum + t[rs(rt)].sum;
}
void down(int l, int r, int x){
int mid = (l + r) >> 1;
if (tag[x] != 0){
tag[ls] += tag[x];
tag[rs] += tag[x];
Min[ls] += tag[x];
Min[rs] += tag[x];
tag[x] = 0;
}
}//lcez_cyc
pair<int,int> query(int A, int B, int l, int r, int x) {
if (A <= l && r <= B)
return make_pair(Min[x], cnt[x]);
down(l, r, x); // 在继续查询之前,先检查是否要下传标记
int mid = (l + r) >> 1, ret = make_pair(0x3F3F3F3F, 0);
if (A <= mid) ret = min(ret, query(A, B, l, mid, ls));//扫描他的左孩子
if (b > mid){
pair<int,int> tmp = min(ret, query(A, B, mid + 1, r, rs)); //扫描他的右孩子
if (tmp.first == ret.first) ret.second += tmp.second;//如果做区间的最小值等于右区间的最小值,就吧个数加起来
else if(tmp.first < ret.first) ret = tmp;//要不然就取更小的那个
}
return ret;
}
总结
如果要用线段树维护一个数据结构,一定要想清楚怎么实现update函数和down函数。
也就是如何合并两个子树的信息,如何解决标记下传。
解决了这两个问题,直接套用线段树的模板就可以了。
SPOJ GSS1 Can you answer these queries I
你有一个长度为 n 的序列 A[1], A[2], …, A[N].
询问:Query(x, y) = max { A[i] + … + A[j]; x <= i <= j <= y}
给出 M 组 (x, y),请给出 M 次询问的答案。
|A[i]| <= 15007, 1 <= N,M <= 50000
自己写
如同线段树,每一段区间(l,r)的最大值由(l,mid)的最小值和(mid+1,r)的最小值以及中间跨过中线的最小值确定。
跨过中线的最小值又等于左边的最大后缀和加上右边的最大前缀和。注意状态转移方程
实现代码
void pre(int rt){
t[rt].max = max(t[ls(rt)].max,t[rs(rt)].max);
t[rt].max = max(t[rt].max,t[ls(rt)].aft + t[rs(rt)].pre);
t[rt].aft = max(t[rt].aft,t[rs(rt)].aft);
t[rt].pre = max(t[rt].pre,t[ls(rt)].pre);
t[rt].sum = t[ls(rt)].sum + t[rs(rt)].sum;//老师写这个干啥???
}
void build(int l,int r,int rt){
if(l == r){
t[rt].max = t[rt].lmax = t[rt].rmax = t[rt].sum = a[l];
return;
}
t[rt].l = l,t[rt].r = r;
int mid = (l + r) >> 1;
build(l,mid,ls(rt));
build(mid + 1,r,rs(rt));
pre(rt);
}
//下面是老师写的有点乱我不想看
void query(int A, int B, int l, int r, int x, int &Smax, int &Lmax, int &Rmax, int &Sum){
if (A <= l && r <= B){
Smax = smax[x];
Lmax = lmax[x];
Rmax = rmax[x];
Sum = sum[x];
return;
}
int mid = (l + r) >> 1;
int smaxl = -1e9, lmaxl = -1e9, rmaxl = -1e9, suml = 0;
int smaxr = -1e9, lmaxr = -1e9, rmaxr = -1e9, sumr = 0;
if (A <= mid) query(A, B, l, mid, ls, smaxl, lmaxl, rmaxl, suml);
if (mid < B) query(A, B, mid + 1, r, rs, smaxr, lmaxr, rmaxr, sumr);
Lmax = max(lmaxl, suml + lmaxr);
Rmax = max(rmaxr, sumr + rmaxl);
Smax = max(max(smaxl, smaxr), rmaxl + lmaxr);
Sum = suml + sumr;
}
SPOJ GSS5 Can you answer these queries V
•你有一个长度为 n 的序列 A[1], A[2], …, A[N].
•询问:
•Query(x1, y1, x2, y2) = max { A[i] + … + A[j]; x1 <= i <= y1, x2 <= j <= y2}
•x1 <= x2, y1 <= y2
•给出 M 组操作,输出每次询问的答案
•|A[i]| <= 10000, 1 <= N,M <= 10000
分类讨论
- y1 < x2
那就直接分三段处理(i,y1)(y1,x2) (x2,j) - y1 >= x2
- i >= x2 && j <= y2
同GSS1 - i < x2 && j > y2
同y1 < y2的讨论 - i < x2 && j <= y2 || i >= x2 && j > y2
同GSS1
- i >= x2 && j <= y2
POJ 3321 Apple Tree
有一颗以 1 为根的树,每个节点上都有一个苹果。
每次有以下两种操作:
C x:x节点上的苹果状态发生了改变。如果原来有苹果,那么被摘了;如果原来没有苹果,那么现在放上去了一个;
Q x:询问以 x节点为根的子树里总共有几个苹果。
N, M <= 100000
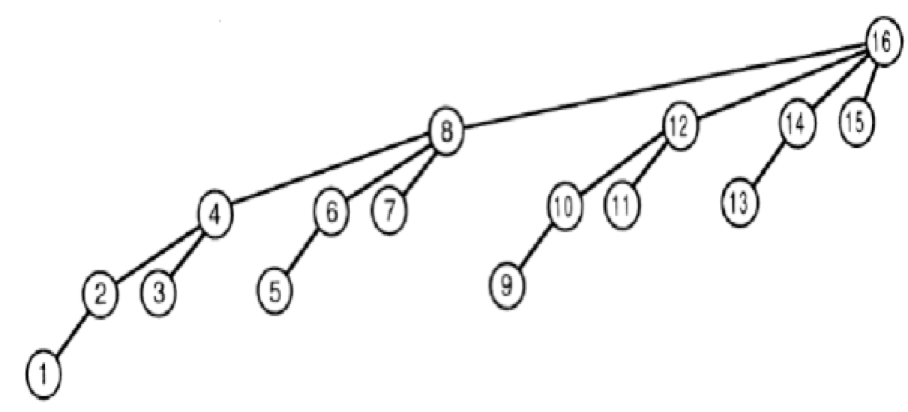
DFS序遍历,给每个点赋值,如下面这个拙劣的图
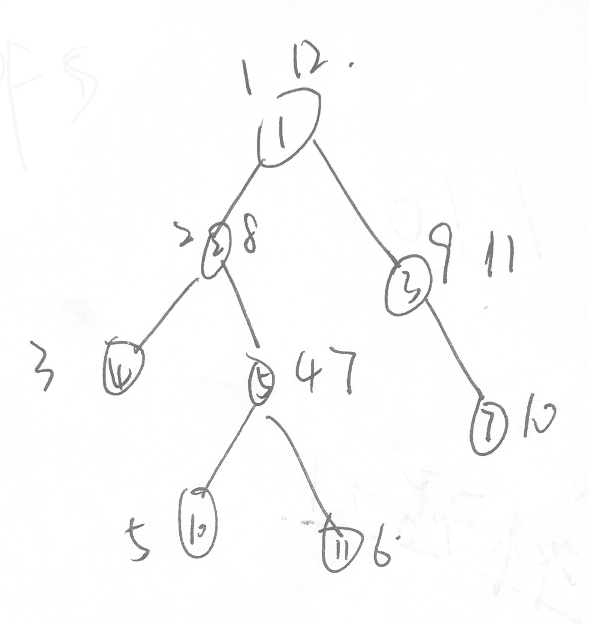
我们给每个节点赋了两个值,如果以这些数字为左右端点建立线段树,区间和就是以这个点为根的树的苹果的个数
HDU3333 TURING 疯狂图灵
•有一个长度为 n 的序列 A[1], A[2], …, A[n]
•每次给出一个询问 (x, y):
•请你求出 A[x .. y] 中出现过的数字之和。(出现多次的数只计算一次)
•n <= 30000, Q <= 100000
好了我明白了
自己写
首先记录一个数组left[i]表示a[i]左边第一个出现相同数字的位置。首先有两个判断:
如果left[i] < x 说明a[i]是第一个出现的,应该加进去。
如果left[i] >= x 说明a[i]不是第一个出现的,不应该加进去
那这样我们举个例子
a 2 3 2 3 2 3 3
left -1 -1 1 2 3 4 5
从小到大枚举 x,把当前 left[i] < x 的 a[i] 插入线段树中的第 i 个位置。
表明:对于任意的 y,询问 [x, y] 的话,如果 i 在 [x, y]中,那一定有 left[i] < x,所以 a[i] 是要被统计进答案的。
这样就做到了 O((n + q) log n) 的时间复杂度,离线解决了所有询问。
枚举区间前端点,然后查找区间后端点,前段点之前的是原数组,前后端点时间的事符合条件的
LCA
定义
给出有根树T中的两个不同的节点u和v,找到一个离根最远的节点x,使得x同时是u和v的祖先,x就是u和v的最近公共祖先 (Lowest common ancestor)
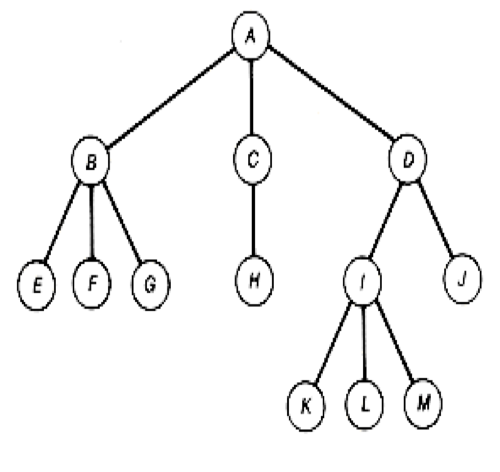
暴力算法
•先从u往根节点遍历,经过的点都打一个标记
•再从v往根节点遍历,路上碰到的第一个打标记的点就是它们的LCA.
•时间复杂度:一次询问是O(n)的,n为树的节点个数。
倍增算法
•记up[u][k]为从u向根走\(2^k\)步到达的节点。
•up[u][0] = fa[u]
•up[u][k] = up[up[u][k – 1]][k – 1] //u向上走\(2^k\)到达的位置就是向上走\(\frac{2^k}2\)再走\(\frac{2^k}2\)得到的。
•我们从大到小枚举k,比较up[u][k]与up[v][k]
•若up[u][k] == up[v][k]
•说明up[u][k]是u和v的公共祖先
•若up[u][k] != up[v][k]
•说明u和v还没有走过LCA
•令u = up[u][k], v = up[u][k]
#include <iostream>
#include <cstdio>
#include <algotirhm>
using namespace std;
int dep[N],up[N][20],f[N];
void dfs(int rt,int fa){
dep[rt] = dep[fa] + 1;
up[rt][0] = fa;
for(int i = 1;1 << i <= dep[rt]; i++){
up[rt][i] = up[up[rt][i-1]][i-1];
}
for(找所有的rt的未访问过的连边){
if(不是父亲节点){
dfs(这个点,fa + 1);
}
}
}
int lca(int a,int b){
if(dep[a] < dep[b]) swap(a,b);
int nowdep = dep[a];
for(int i = 20;i >= 0; i--){
if(nowdep - (1 << i) >= dep[b]){
a = up[a][i];
nowdep -= 1 << i;
}
}
for(int i = 20;i >= 0; i--){
if(up[a][i] != up[b][i])
continue;
else
a = up[a][i],b = up[b][i];
}
return a;
}
int main(){
啥都不写我就不会有错
return 0;
}
时间复杂度
预处理:
fa数组:通过dfs或bfs遍历一遍树得到,O(n)
up数组:第一层大小为n,第二层大小为log n,故为O(n log n)
每次询问:
两个点向上爬的次数是O(log n)的。
于是我们在O(n log n) – O(log n)的时间复杂度下完美的解决了LCA问题,且倍增算法是在线的。
后续我们将介绍两个时间复杂度更优秀的在线和离线做法。
邻接矩阵存图
ST表
描述
•运用倍增的思想,我们令f[i][k]数组表示区间[i, i + 2k - 1]中的最小值
•显然有
•f[i][0] = a[i]
•f[i][k + 1] = min(f[i][k], f[i + (1 << k)][k])
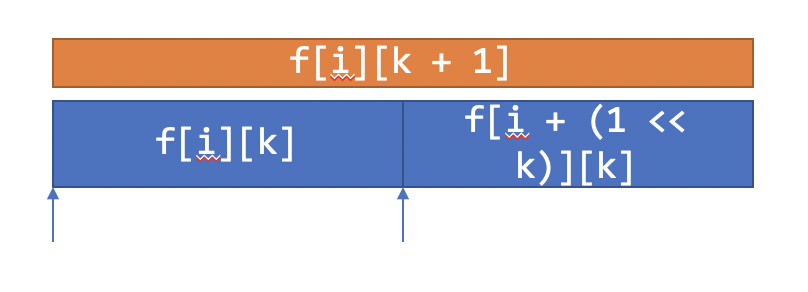
查询
•查询时给了一个区间[l, r],我们找一个最大的j满足2j <= r - l + 1 (因为如果不是2j,就会导致前后的ST表不能覆盖区间)
•于是我们可以用f[l][j]和f[r – 2j + 1][j]来覆盖这个区间,得到最小值
•也即answer = min(f[l][j], f[r – (1 << j) + 1][j])
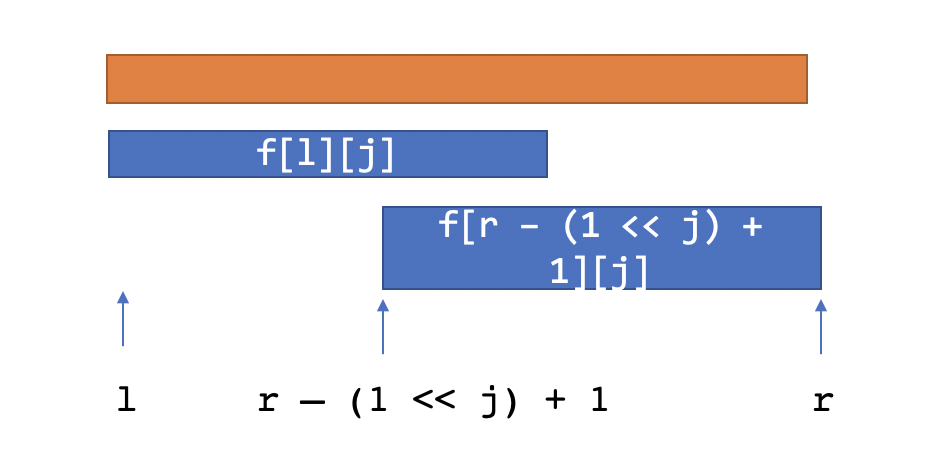
树状数组
描述
•与线段树类似,树状数组也是用于动态查询区间信息、支持修改的数据结构。
•与线段树相比,它更简洁,实现起来也更方便,但是它能维护的信息比较有限。也送一扩展到高维度
•树状数组是在 1994 年由 Peter M. Fenwick 在他的论文《A New Data Structure for Cumulative Frequency Tables》中率先提出的,所以又称 Fenwick Tree。
先看看二位前缀和
首先有
则递推公式为
直角坐标系中\((x_1+1,y_1+ 1 )\)和\((x_2,y_2)\)的矩阵和
树状数组的思想
每个正整数都可以表示为若干个 2 的幂次之和。
类似的,每次求前缀和,我们也希望将区间 [1,i] 分解成 log2 i 个子集的和。
也就是如果 i 的二进制表示中如果有 k 个 1,我们就希望将其分解为 k 个子集之和。
代码
get_index(v):
i = 0
len = n
while len != 0:
test_id = i + len
if (v >= sum[test_id]):
i = test_id
v -= sum[test_id]
len /= 2
return i
例题3(POJ2352)
•二维平面上有 n 个点 (x[i], y[i])。
•现在请你求出每个点左下角的点的个数。
•n <= 15000, 0 <= x, y <= 32000//扫描线
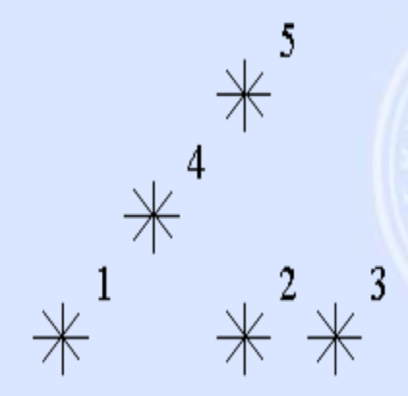
•具体来说,我们从小到大枚举 y 坐标。
•每次把 y 坐标小于等于当前枚举值的点的横坐标 x 插入 S 集合。
•对于一个点 (x[i], y[i]) (y[i]等于当前枚举的y坐标),它左下角的点的个数等于 S 中小于等于 x[i] 的个数。
•只需要用树状数组来维护 S 集合中的数。
•插入一个 x,就把 add(x, 1)
•查询的时候,把 query(x[i]) 加入答案即可。
•时间复杂度是 O(n log n)。


