#QBXT2020寒假 Day 3
STL
VECTOR动态数组
语句
定义方式:vector
在末尾压入容器:a.push_back(x);
在末尾弹出容器:a.pop_back();
清空容器:a.clear();
查询元素个数:a.size();
首指针:a.begin();
插入元素在sit位置:a.insert(sit,x);其中sit是vector的迭代器。
其它像数组一样调用就可以了。
看做是一个动态数组
复杂度
访问,添加啥的都是\(o(1)\),但是常数比较大
栈和队列
语句
定义:stack
查询栈顶:a.top();
压入栈顶:a.push(x);
将元素从栈顶弹出:a.pop();
查询a中的元素个数:a.size();
清空只能慢慢pop。
队列
定义:queue
插入队尾:a.push(x);
删除队首:a.pop();
查询队尾:a.back();
查询队首:a.front();
查询长度:a.size();
清空只能慢慢pop。
用栈写队列WTF
因为进栈出栈的时间复杂度都是O(1)的
加入的时候先进A再进B
时间复杂度为O(n)
MAP
•映射,把它看做一个无限大的数组。
•定义方式:map<int ,int> a;
•使用方式:a[x]++,cout<<a[y]等。
•利用迭代器查询map里的所有二元组:
•for (map<int,int>::iterator sit=a.begin(); sit!=a.end(); sit++) cout<
•清空:a.clear();
SET平衡树(二叉搜索树)
•定义:set
•插入元素:a.insert(100);
•清空set:a.clear();
•查询set中有多少元素:a.size();
•查询首元素:a.begin(),返回iterator。
•查询最后一个元素+1:a.end(),返回iterator。
•删除:a.erase(sit); sit是一个iterator类型的指针或者是元素值。
•判断是否有数字100:a.count(100)。
退化是什么操作
哈希???
上面的是平衡树实现的MAP,还有用哈希实现的MAP
老师讲了,我放弃了,去水群了。
今天的节目到此结束,我们下期再见👋
二叉搜索树
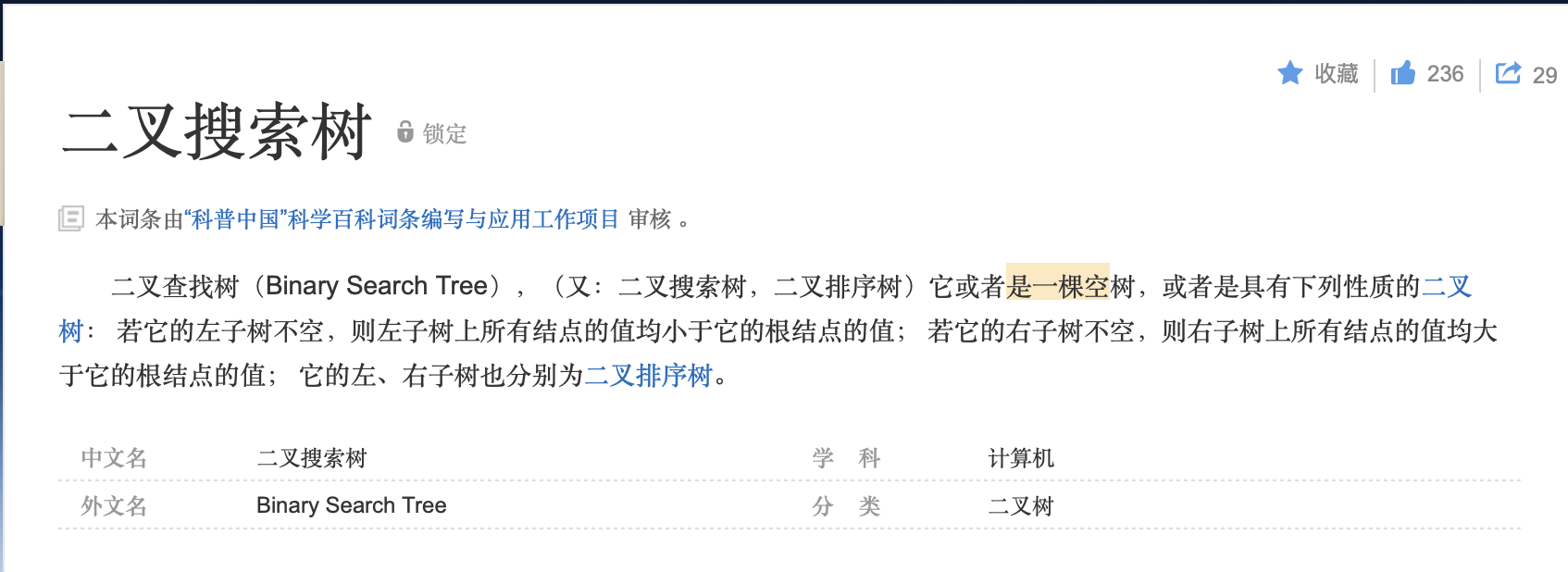
描述
如图所示,一颗二叉查找树是按二叉树结构来组织的。
这样的树可以用链表结构表示,其中每一个节点都是一个对象。
节点中包含 key, left, right 和 parent。
如果某个儿子节点或父节点不存在,则相应域中的值即为 NULL。
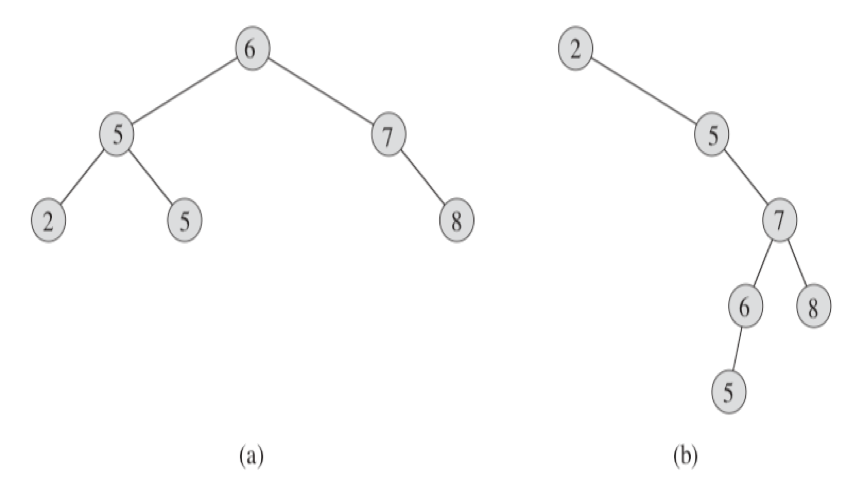
设 x 为二叉查找树中的一个节点。
如果 y 是 x 的左子树的一个节点,则 key[y] <= key[x].
如果 y 是 x 的右子树的一个节点,则 key[x] <= key[y].
中序遍历
根据二叉查找树的性质,可以用一个递归算法按排列顺序输出树中的所有关键字。这种算法称为中序遍历算法。
因为子树根的关键字在输出时介于左子树和右子树的关键值之间。
inorder(x):
if x != NULL:
inorder(left[x]);
print key[x];
inorder(right[x]);
只要调用inorder(root[T]),就可以输出一颗二叉查找树 T 中的全部元素。
查询操作
查询k,如果k的值大于根节点,就右节点,如果k的值小于根节点,就左节点
时间复杂度O(树的高度)
给定指向树根的指针和关键字 k,过程 Tree-Search 返回指向包含关键字 k 的节点(如果存在的话)的指针;否则,返回 NULL
Tree-Search(x, k)
if x == NULL or k == key[x]:
return x
if k < key[x]:
return Tree-Search(left[x], k)
else
return Tree-Search(right[x], k)
试试模拟一下 Tree-Search(root, 13)
查询最小(大)元素
要查询二叉树中具有最小关键字的元素,只要从根节点开始,沿着各节点的 left (right)指针查找下去,直到遇到 NULL 为止。
ree-Minimum(x):
while left[x] != NULL:
x = left[x]
return x
二叉查找树的前驱和后继?
给定一个二叉查找树中的节点,有时候要求找出在中序遍历顺序下它的后继。
如果所有的关键字均不相同,则某一结点 x 的后继即具有大于 key[x] 中的关键字中最小者的那个节点。
根据二叉查找树的结构,不用对关键字做任何比较。
Tree-Successor(x):
if right[x] != NULL:
return Tree-Minimum(right[x])
y = parent[x]
while y != NULL and x = right[y]:
x = y
y = parent[y]
return y//lcez_cyc
插入操作??
•为将一个新值 v 插入到二叉查找树 T 中,可以调用Tree-Insert。
•传给该过程的参数是个节点 z,并且有 key[z] = v, left[z] = NULL, right[z] = NULL,该过程修改 T 和 z 的某些域,并把 z 插入到树中合适的位置上。
Tree-Insert(T, z):
y = NULL, x = root[T]
while x != NULL:
y = x
if (key[z] < key[x]) x = left[x]; else x = right[x]
parent[z] = y
if y == NULL then root[T] = z
else if key[z] < key[y] then left[y] = z
else right[y] = z
删除??算了吧
但是
我们已经知道,二叉查找树上的各基本操作的运行时间都是O(h),h 为树的高度。
但是随着元素的插入或删除,树的高度会发生变化。
例如,如果各元素按严格增长的顺序插入,那么构造出的树就是一个高度为 n - 1 的链。
如果各元素按照随机的顺序插入,则构造出的二叉查找树的期望高度为 O(log n)。
这里省略证明,但这是一个重要的结论。
当看见题目中出现“数据是随机构造的”时,要能够记起这个结论哦!
堆 HOPHEAP
根节点比他的孩子节点都小的是小根堆,都大的是大根堆
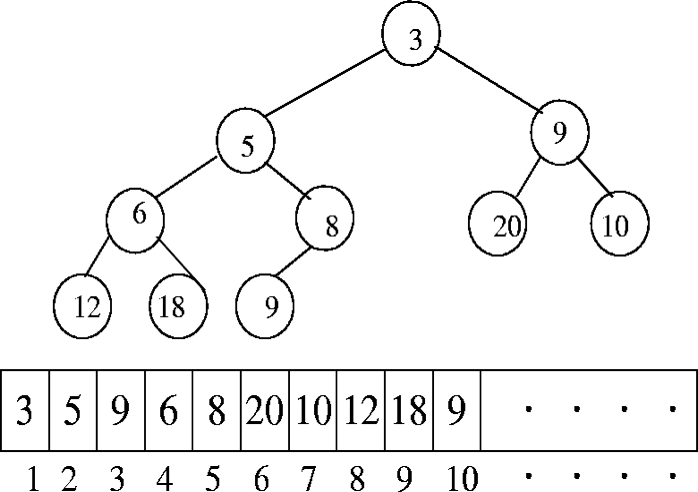
删除堆顶元素
先删除堆顶的位置,再找一个他更小的儿子替代他的位置,如此递归
插入操作
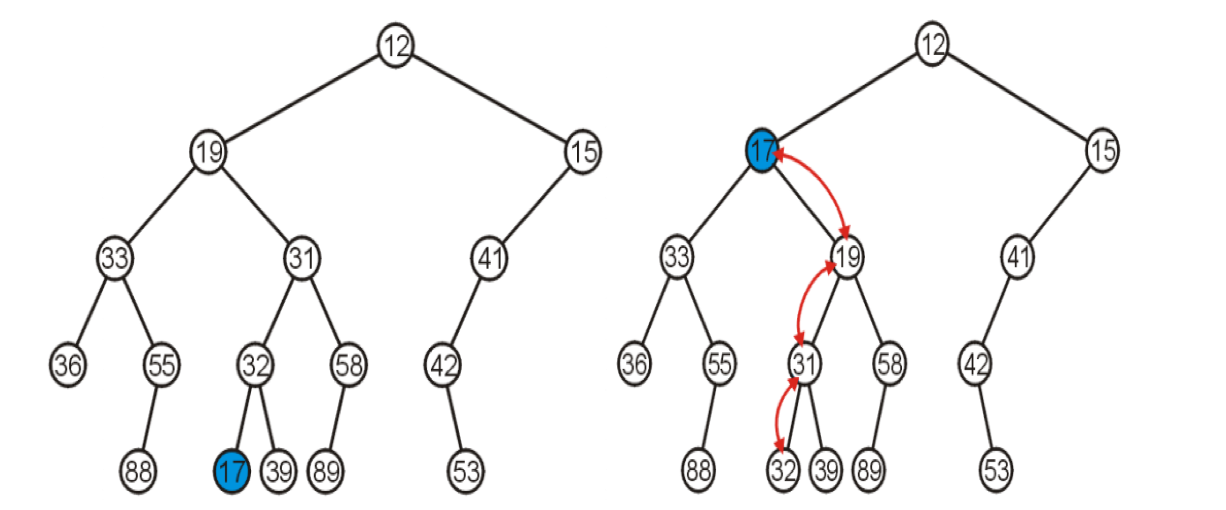
从堆底部插入,不断和比他大的他的父亲节点交换,直到他大于父亲节点
代码实现
定义:priority_queue <int> a;
插入队尾:a.push(x);
删除队首:a.pop();
查询队首:a.top():O(1)
清空只能慢慢pop。
最小堆与二叉搜索树的区别
对于二叉搜索树的任意一个节点:
-
左子树的值都小于这个节点的值
-
右子树的值都大于这个节点的值
-
两个子树都是二叉搜索树
对于最小堆的任意一个节点:
-
所有的子节点值都大于这个节点的值
-
两个子树都是最小堆
例题1 序列合并
给出两个长度为 n 的有序表 A 和 B,在 A 和 B 中各任取一个元素,可以得到 \(n^2\) 个和,求这些和中最小的 n 个。
n <= 400000
固定 A[i], 每 n 个和都是有序的:
A[1] + B[1] <= A[1] + B[2] <= … <= A[1] + B[n]
A[2] + B[1] <= A[2] + B[2] <= … <= A[2] + B[n]
…
A[n] + B[1] <= A[n] + B[2] <= … <= A[n] + B[n]
a[1]b[1]是最小的,第二小的可能是a[1]b[2],a[2]b[1]。就每次把这一个点右边下边的数字压进去,然后依次弹出,直到找全前n小的数字。
或者把这n个队列的第一个元素压入堆,每次弹出一个,并把这个数字所在的队列的后面的数字压进去,直到找到全前n小的数字。
例题二 丑数
丑数是指质因子在集合 {2, 3, 5, 7} 内的整数,第一个丑数是 1.现在输入 n,输出第 n 大的丑数。
n <= 10000.
先将2 3 5 7入堆
先有最小的四元组(a,b,c,d),弹出最小的\(2^a3^b5^c7^d\)然后压入(a + 1, b, c, d) (a, b + 1, c, d) (a, b, c + 1, d) (a, b, c, d + 1) ,堆顶有相同元素就和POP掉就好
POJ3784
•假设当前数组长度为 2k + 1,考虑维护 3 个序列:
当前最小的 k 个数
中位数 mid
当前最大的 k 个数
•接下来会插入一个数 x:
•如果x >= mid,就把 mid 插入第一个序列,把 x 插入第三个序列
•如果x < mid,就把 x 插入第一个序列,把 mid 插入序列。
•现在数组长度为 2k + 2,3 个序列分别为:
当前最小的 k + 1 个数
[空]
当前最大的 k + 1 个数
•接下来会再插入一个数 x:
•如果 x 大于等于 1 号序列的最大值,就把 x 插入 3 号序列,然后把 3 号序列的最小值删除,插入 2 号序列作为中位数。
•如果 x 小于 1 号序列的最大值,就把 x 插入 1 号队列,然后把 1 号队列的最大值删除,插入 2 号序列作为中位数。
•时间复杂度 O(n log n).


