#QBXT2020寒假 Day2下午
Day 2
二分
描述
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
例题:
昨天考试的T2 就是YRQ神仙70分的那个
优越性
二分相对于暴力枚举来讲,判定次数会显著变少
具体来说,如果暴力枚举期望是O(N)次
那么二分只需要O(logN)次就可以得出答案
一般来说我们会在以下情况用到二分:
求单调函数的零点
求一堆东西的最小值最大是多少
很难直接算出答案,但是很好判定答案合不合法
实现代码
while(r-l>eps)
{
mid=(l+r)/2;
if(f(mid)>0) r=mid;
else l=mid;
}
while(l<r)
{
mid=(l+r)/2;
if(f(mid)>0) r=mid;
else l=mid+1;
}//lcez_cyc
派
我的生日要到了!根据习俗,我需要将一些派分给大家。我有N个不同口味、不同大小的派。有F个朋友会来参加我的派对,每个人会拿到一块派(必须一个派的一块,不能由几个派的小块拼成;可以是一整个派)。
我的朋友们都特别小气,如果有人拿到更大的一块,就会开始抱怨。因此所有人拿到的派是同样大小的(但不需要是同样形状的),虽然这样有些派会被浪费,但总比搞砸整个派对好。当然,我也要给自己留一块,而这一块也要和其他人的同样大小。
请问我们每个人拿到的派最大是多少?每个派都是一个高为1,半径不等的圆柱体。
二分一下每个人拿到的派的大小
然后整体扫一遍N个派,由于每个人派的大小已知,那么每个初始的派能切成的块数就也能知道了
检验一下这些派够不够分
如果不够,说明每个人拿的派太大了,往小了二分
如果够,说明每个人可能还可以拿更多的派,往大了二分
最大值最小化
把一个包含n个正整数的序列划分为m个连续的子序列(每个正整数恰好属于一个序列)。设第i个序列的各数之和为S(i),你的任务是让所有S(i)的最大值尽量小。
例如序列1 2 3 2 5 4划分成3个序列的最优方案为1 2 3|2 5 |4,其中S(1)、S(2)、S(3)分别为6、7、4,最大值为7;如果划分成1 2|3 2|5 4,则最大值为9,不如刚才的好。
n<=10^6,所有数之和不超过10^9。
先二分一下最大值是多少
这个值是每一段总和的上限
然后贪心,只要总和在这个限度内就不断地往里添加后面的数,直到不能添加为止,那么这些数就组成了一段
扫完所有的数之后,看一看划分出了几段
如果段数>m,说明这个最大值设得太小了,应该变大,l=mid+1
否则说明最大值还有可能变小,r=mid
排干水塘
公园里有n个水塘,需要把这n个水塘中的水排干,水塘中的水在自然条件下1个单位的时间可以蒸发A升水。现在买了1台抽水机,使用抽水机可以让你用1个单位的时间使每个水塘除开自然蒸发的A升水外,还可抽B升水,但在1个单位的时间内只能对1个水塘使用。
要你求出排干所有水塘的最少时间(水塘中的水为0时为排干)。
公园里有n个水塘,需要把这n个水塘中的水排干,水塘中的水在自然条件下1个单位的时间可以蒸发A升水。现在买了1台抽水机,使用抽水机可以让你用1个单位的时间使每个水塘除开自然蒸发的A升水外,还可抽B升水,但在1个单位的时间内只能对1个水塘使用。
要你求出排干所有水塘的最少时间(水塘中的水为0时为排干)。
二分时间T,把每一个水塘减去已经蒸发的,再把剩下的水除以b,最后看看这个时间是否大于T。大于,说明T小了,反之,T大了。
序列积第 n 小元素
给出两个长度为n的数组A和B, 在A和B中各任取一个, 可以得到n×n个积. 求第m小的元素。
n<=100000
自己写的
确定一个ai,看看有没有bi = x/ai
所有小于bi的数的个数都加起来
找下一个ai
再加
直到x/ai < b1
啊差不多就这样。
复杂度\(O(n^2\log n)\)
还有优化
从小到大排序:
有:随着i变大,\(\frac{x}{a_i}\)变小,即符合要求的\(b_i\)便小。设每次b的下标为\(y_j\),则\(y_j\)递减
则找一个指针记录y,从1到n,每更新一次i,y就减小到满足\(a_i \times b_y <= x\)的最大值,这样的复杂度为\(O(n\log n)\).
代码
bool check(int x){
int ans = 0;
int cnt = n;
for(int i = 1;i <= n; i++){
while(x/b[cnt] > a[i]) cnt--;
ans += cnt;
}
return ans == mid;
}//lcez_cyc
跳石子!!!
二分答案。回头写了再说吧
01分数规划!!!!
Poj2728
大意是:给你一个价值a[i]和代价b[i],然后我们选举n-k个物品,使得总价值/总代价最大。
二分答案x,寻找符合条件的情况,使得
那么可以有c[i]数组,使得
最终检查是否合法的时候即需要
bool check(int x)
{
for(int i=1;i<=n;++i)
c[i]=a[i]-b[i]*x;
sort(c+1,c+1+n);
int sum=0;
for(int i=1;i<=k;++i)
sum+=c[i];
return sum<=0;
}
int main()
{
int l,r;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid))ans=mid,r=mid+1;
else l=mid+1;
}//可以开一个ans不用后续找答案
return 0;
}
Desert King

设权值设为\(a_i= cost_i - len_i\),则求其最小生成树。
分治算法
描述
分治就是“分而治之”
他可以把一个复杂的问题简单化,从全局变成局部,逐渐缩小问题的规模,更加高效的解决问题
高效
快速排序(分治+冒泡排序)
归并排序(标准分治)
都是用了分治的思想把时间从\(O(N^2)\)变成了\(O(N \log N)\)
复杂度计算
主定理

其实和线段树一样吧。应该是线段树的两倍。
逆序对
爽啊上链接
先再看看想想这个思路:
直接暴力求的话,显然时间复杂度是不可接受的
我们不妨转换一下,分而治之
把整个数列劈成两半
则总的逆序对数量=左半部分逆序对数量+右半部分逆序对数量+左边的数比右边大的对数
前两项我们可以递归求解,最后一项我们可以在归并排序的同时稍加处理,O(N)计算出来
这样时间复杂度与归并排序一样,都是O(NlogN)的
//手糊一下
void msort(int l,int r){
if(l == r) return;
int mid = (l + r) >> 1;
msort(l,mid);
msort(mid+1,r);
int x = l,y = mid+1;
int cnt = l;
while(x <= mid && y <= r){
while(a[x] < a[y] && x <= mid) d[cnt++] = a[x++];
while(a[x] > a[y] && y <= r) d[cnt++] = a[y++];
ans += y-l;
}
for(int i = l;i <= r; i++)
a[i] = d[i];
}
快速幂 (这个要回头看!!)
棋盘覆盖(去洛谷看!!)
直接做好像并不可行,我们考虑逐渐把问题简化
先假设迷宫是一个2*2的方格,那么方案就很简单了:把公主没站的三个格子铺上地毯就OK了
现在想44的方格,我们把它划分成4个22的方格,公主必然站在其中之一,所以那个22的方格的铺地毯方式就可以递归求出了。对于其他三个22的格子,我们先铺一个跨过他们三个的地毯,然后把这块地毯想象成三个公主,我们就可以递归求解了
接着再想88的方格,我们把它划分成4个44的方格,公主必然站在其中之一,所以那个44的方格的铺地毯方式就可以递归求出了。对于其他三个44的格子,我们先铺一个跨过他们三个的地毯,然后把这块地毯想象成三个公主,我们就可以递归求解了
第k小元素!!
给你一个长度为N的序列,要求你求出其中的第k小元素
1<=K<=N<=2000000
不可以直接排序再找第k小,这道题只允许O(N)算法
类似快速排序,我们先随机找到一个值,然后扫一遍整个序列,这样可以统计出比他大的数的个数X和比他小的数的个数Y,以及跟他相等的个数Z
如果K<=Y,那我们不用管后半部分,第K小元素一定在这些数当中,递归即可
如果Y<k<=Y+Z,那这个元素就是第K小
如果Y+Z<k,那我们不用管前半部分,第K小元素一定在后面的那些数中,我们要找那X个数中的第K-(Y+Z)个元素
由于值是随机选取的,我们可以认为他把原数列分成差不多相等的两部分
所以T(N)=O(N)+T(N/2),算法是O(N)的
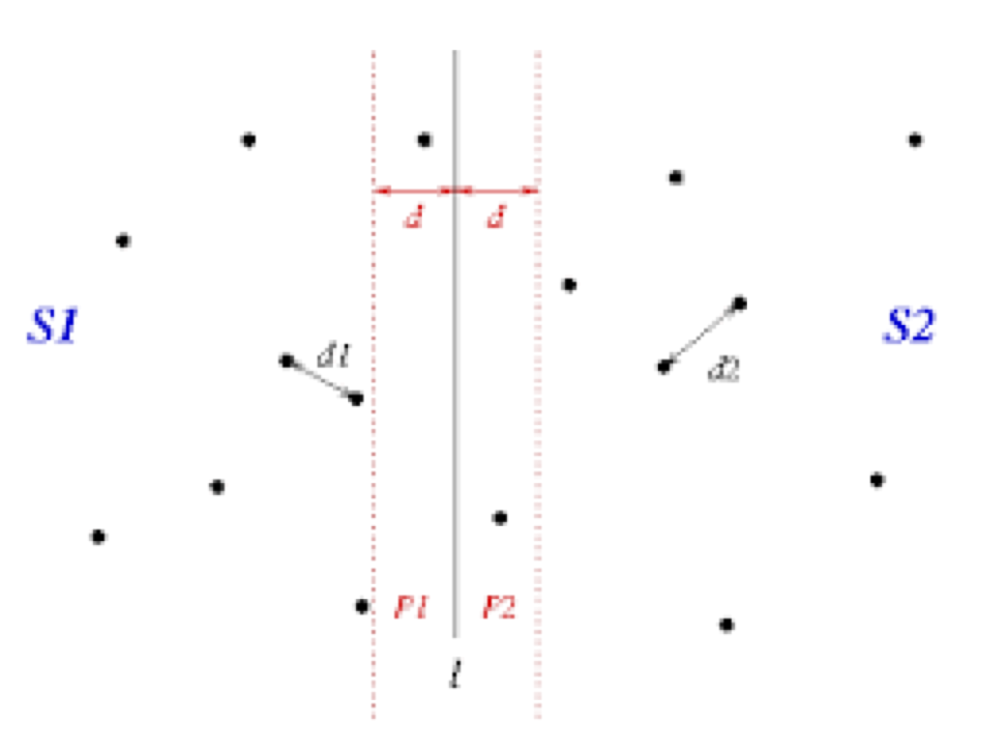
平面最近点对
平面上有n个点,求出所有点对的欧几里得距离最小的点对
分治。每次的d = min(左边的最小值,右边的最小值,左右区间最近的值)
左右区间最近的值怎么搞?
首先得到x = min(左边最小值,右边最小值)
对所有的点按照x坐标(或者y)从小到大排序 😦 。
根据下标进行分割,使得点集分为两个集合。
递归的寻找两个集合中的最近点对。
取两个集合最近点对中的最小值
最近距离不一定存在于两个集合中,可能一个点在集合A,一个点在集合B,而这两点间距离小于dis。
牛跳房子
USACO 15 FEB 回头自己看老师没讲


