结对项目作业——求交点
| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里 | 结对项目作业 |
| 我在这个课程的目标是 | 学习软工的思想方法,写出好的软件并维护 |
| 这个作业在哪个具体方面帮助我实现目标 | 学习了如何封装core,如何编写动态库并在另一个项目中引用,同时初步接触结对编程,认识到了这种开发方式的优缺点。 |
| 班级 | 006 |
| 项目地址(可以看到提交记录以及tag的地址) | githubProcess |
| 项目地址(最终的可运行版本,方便助教clone) | githubFinal |
一、PSP时间记录
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 1420 | 1700 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 600 | 600 |
| · Design Spec | · 生成设计文档 | 90 | 120 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 10 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 40 | 60 |
| · Design | · 具体设计 | 40 | 80 |
| · Coding | · 具体编码 | 400 | 520 |
| · Code Review | · 代码复审 | 20 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 240 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 30 | 15 |
| · Size Measurement | · 计算工作量 | 30 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 5 |
| 合计 | 1420 | 1700 |
二、看 Design by Contract,Code Contract 的内容,描述这些做法的优缺点,说明你是如何把它们融入结对作业中的。
首先我先说一下我对契约式设计的一点理解(代码协定)。
契约式设计的主要目的是希望程序员能够在设计程序时明确地规定一个模块单元(具体到面向对象,就是一个类的实例)在调用某个操作前后应当属于何种状态。说白了我的理解是这是一种语法的规范。
契约式设计强调三个概念:前置条件,后置条件和不变式。前置条件发生在每个操作(方法,或者函数)的最开始,后置条件发生在每个操作的最后,不变式实际上是前置条件和后置条件的交集。违反这些操作会导致程序抛出异常。
其优点主要是提高了程序的可靠性;让你的设计更系统,更清楚,更简单;方便调试。
缺点有要完成契约式设计需要学习其思想和技术,需要花不少时间;撰写成本变高,可能以前的一句话现在要写好几句;只有大量的实践才能写出好的契约式代码,那么很可能前面写的代码是四不像的,还浪费了时间。
我在写核心部分的时候,只在每一个函数的开始除,会对输入的数据进行一些合法性的判断,后置条件和不变式并没有理解出应该怎么使用,也不知道这样算不算应用了这种思想。
由于没有系统的学习过这种编程的思想方法,所以在这次的作业上并没有体现出多少。
三、计算模块接口的设计与实现过程
1.新增功能介绍
本次新增的功能为支持线段和射线这种几何体加入到交点的计算中,下面来分析加入这两个新的几何体后,程序需要做的改变。
首先,在读入一个几何体的数据后,先判断是什么,如果是射线,它的方程和直线是一样的,记做$ Ax+By+c=0 $
除此以外,记录其发射点为(x1, y1),同时记录射线的射出方向dirct,这里有四个方向:向左,向右,垂直向上,垂直向下;如果是线段,方程也记为:$ Ax+By+c=0 $,同时记录其两个顶点分别为(x1, y1) , (x2, y2);其他的直线和圆处理同上一次,不再赘述。
之后就是计算的过程了,大体的思路还是一样的,几何体间两两求交点,首先是线与线之间,先联立两条线的方程,如果是平行的直接返回,如果有交点,则要判断这个交点是否在两条线上。如果是两条直线,那么一定在,将其加入set中,如果是一条直线和一条射线,只需判断求出的点是否在射线上即可,这里用到函数is_on_ray(Line l, crosspoint point),如下:
bool is_on_ray(Line l, crosspoint point)
{//射线的交点问题
if (l.dirct == 0) {
if (point.x >= l.x1) {
return true;
}
else {
return false;
}
}
else if (l.dirct == 1) {
if (point.x <= l.x1) {
return true;
}
else {
return false;
}
}
else if (l.dirct == 2) {
if (point.y >= l.y1) {
return true;
}
else {
return false;
}
}
else {
if (point.y <= l.y1) {
return true;
}
else {
return false;
}
}
}
思路大体如下,如果射线的方向向右,那么这个求出的交点的横坐标只要大于等于射线的顶点的横坐标即可,同理射线向右时交点横坐标要小于等于顶点的横坐标,向下时交点的纵坐标要小于等于顶点的纵坐标,向上时交点的纵坐标要大于等于顶点的纵坐标。
通过这个函数我们可以判断交点是否在射线上。
继续上文,若是两条线是一条直线和一条线段,那么只需要判断交点是否在线段上即可,这里用到另一个函数is_on_segment(Line l, crosspoint point),代码如下:
bool is_on_segment(Line l, crosspoint point)
{//直线和线段的交点问题
if (l.x1 == l.x2) {
if (point.y >= l.y1 && point.y <= l.y2) {
return true;
}
else {
return false;
}
}
else {
if (point.x >= l.x1 && point.x <= l.x2) {
return true;
}
else {
return false;
}
}
}
这里的思想是,如果这条线段不是垂直于x轴的,那么交点的横坐标必须大于等于左顶点的横坐标且小于等于右顶点的横坐标,如果是垂直的,那么交点的纵坐标必须大于等于下顶点的纵坐标且小于等于上顶点的纵坐标。
通过这个函数我们可以判断交点是否在线段上。
继续上文,除了之前说的三种情况,还有射线与射线的交点不仅要在第一条射线上,还得在第二条射线上,射线与线段,线段与线段同理,不再赘述。
可以看到新的calculate_line_line如下:
int Intersect::calculate_line_line(Line l1, Line l2)
{//caculate the crosspoint of the two lines
//int is eazy to test
crosspoint point;
if ((l1.A * l2.B == l1.B * l2.A) && (l1.A * l2.C != l2.A * l1.C) && l1.A != 0 && l2.A != 0) {//平行但不重合
return 0;
}
else if ((l1.A * l2.B == l1.B * l2.A) && (l1.B * l2.C != l2.B * l1.C) && l1.B != 0 && l2.B != 0) {
return 0;
}
else if ((l1.A * l2.B == l1.B * l2.A) && (l1.A * l2.C == l2.A * l1.C) && l1.A != 0 && l2.A != 0) {
if (l1.type == 1) {
if (l2.type == 1) {
if (l1.x1 == l2.x1 && l1.y1 == l2.y1) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else {
if (l1.x1 == l2.x1 && l1.y1 == l2.y1) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else if (l1.x1 == l2.x2 && l1.y1 == l2.y2) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
}
else {
if (l2.type == 1) {
if (l1.x1 == l2.x1 && l1.y1 == l2.y1) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else if (l1.x2 == l2.x1 && l1.y2 == l2.y1) {
point.x = l1.x2;
point.y = l1.y2;
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else {
if (l1.x1 == l2.x2 && l1.y1 == l2.y2) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else if (l1.x2 == l2.x1 && l1.y2 == l2.y1) {
point.x = l1.x2;
point.y = l1.y2;
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
}
}
else if ((l1.A * l2.B == l1.B * l2.A) && (l1.B * l2.C != l2.B * l1.C) && l1.B != 0 && l2.B != 0) {
if (l1.type == 1) {
if (l2.type == 1) {
if (l1.x1 == l2.x1 && l1.y1 == l2.y1) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else {
if (l1.x1 == l2.x1 && l1.y1 == l2.y1) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else if (l1.x1 == l2.x2 && l1.y1 == l2.y2) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
}
else {
if (l2.type == 1) {
if (l1.x1 == l2.x1 && l1.y1 == l2.y1) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else if (l1.x2 == l2.x1 && l1.y2 == l2.y1) {
point.x = l1.x2;
point.y = l1.y2;
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else {
if (l1.x1 == l2.x2 && l1.y1 == l2.y2) {
point.x = l1.x1;
point.y = l1.y1;
Setpoint.insert(point);
return 1;
}
else if (l1.x2 == l2.x1 && l1.y2 == l2.y1) {
point.x = l1.x2;
point.y = l1.y2;
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
}
}
else {
point.y = (l1.A * l2.C - l1.C * l2.A) / (l1.B * l2.A - l1.A * l2.B);
if (l1.A == 0) {
point.x = (-l2.C - point.y * l2.B) / l2.A;
}
else {
point.x = (-l1.C - point.y * l1.B) / l1.A;
}
//线段,射线特判
if (l1.type == 0 && l2.type == 0) {
Setpoint.insert(point);
return 1;
}
else if (l1.type == 0 && l2.type == 1) {
if (is_on_ray(l2, point)) {
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else if (l1.type == 0 && l2.type == 2) {
if (is_on_segment(l2, point)) {
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else if (l1.type == 1 && l2.type == 0) {
if (is_on_ray(l1, point)) {
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else if (l1.type == 1 && l2.type == 1) {
if (is_on_ray(l1, point) && is_on_ray(l2, point)) {
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else if (l1.type == 1 && l2.type == 2) {
if (is_on_ray(l1, point) && is_on_segment(l2, point)) {
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else if (l1.type == 2 && l2.type == 0) {
if (is_on_segment(l1, point)) {
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else if (l1.type == 2 && l2.type == 1) {
if (is_on_segment(l1, point) && is_on_ray(l2, point)) {
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
else {
if (is_on_segment(l1, point) && is_on_segment(l2, point)) {
Setpoint.insert(point);
return 1;
}
else {
return 0;
}
}
}
}
接下来是线与圆,其他的逻辑是一样的,区别在于求出了交点后要判断是否在射线或者线段上,如果在才将这个点加入set。
下面是新的calculate_line_circle:
int Intersect::calculate_line_circle(Line l, Circle c)
{
crosspoint point1;
crosspoint point2;
if (l.aNotExist) {
point1.x = l.t;
point2.x = l.t;
double k = ((double)l.t - c.m) * ((double)l.t - c.m);
double r2 = (double)c.r * c.r;
double left = r2 - k;
if (left < 0) {//no result
return 0;
}
else if (left == 0) {//one result
point1.y = c.n;
if (l.type == 0) {
Setpoint.insert(point1);
return 1;
}
else if (l.type == 1) {
if (is_on_ray(l, point1)) {
Setpoint.insert(point1);
return 1;
}
else {
return 0;
}
}
else {
if (is_on_segment(l, point1)) {
Setpoint.insert(point1);
return 1;
}
else {
return 0;
}
}
}
else {//two result
point1.y = sqrt(left) + c.n;
point2.y = c.n - sqrt(left);
if (l.type == 0) {
Setpoint.insert(point1);
Setpoint.insert(point2);
return 2;
}
else if (l.type == 1) {
int num = 0;
if (is_on_ray(l, point1)) {
Setpoint.insert(point1);
num++;
}
if (is_on_ray(l, point2)) {
Setpoint.insert(point2);
num++;
}
return num;
}
else {
int num = 0;
if (is_on_segment(l, point1)) {
Setpoint.insert(point1);
num++;
}
if (is_on_segment(l, point2)) {
Setpoint.insert(point2);
num++;
}
return num;
}
}
}
else {//ax^2+bx+t=0
double a = l.a * l.a + 1;
double b = 2 * ((l.b - c.n) * l.a - c.m);
double t = (double)c.m * c.m + (l.b - c.n) * (l.b - c.n) - (double)c.r * c.r;
double deta = b * b - 4 * a * t;
if (deta > 0) {
point1.x = (sqrt(deta) - b) / (2 * a);
point2.x = (-1 * sqrt(deta) - b) / (2 * a);
point1.y = l.a * point1.x + l.b;
point2.y = l.a * point2.x + l.b;
if (l.type == 0) {
Setpoint.insert(point1);
Setpoint.insert(point2);
return 2;
}
else if (l.type == 1) {
int num = 0;
if (is_on_ray(l, point1)) {
Setpoint.insert(point1);
num++;
}
if (is_on_ray(l, point2)) {
Setpoint.insert(point2);
num++;
}
return num;
}
else {
int num = 0;
if (is_on_segment(l, point1)) {
Setpoint.insert(point1);
num++;
}
if (is_on_segment(l, point2)) {
Setpoint.insert(point2);
num++;
}
return num;
}
}
else if (deta == 0) {
point1.x = (b == 0) ? 0 : -1 * b / (2 * a);
point1.y = l.a * point1.x + l.b;
if (l.type == 0) {
Setpoint.insert(point1);
return 1;
}
else if (l.type == 1) {
if (is_on_ray(l, point1)) {
Setpoint.insert(point1);
return 1;
}
else {
return 0;
}
}
else {
if (is_on_segment(l, point1)) {
Setpoint.insert(point1);
return 1;
}
else {
return 0;
}
}
}
else {
return 0;
}
}
}
圆和圆的交点逻辑没有任何变化,不再赘述。
2.设计的接口概述
public:
void clear();
void readdata();
void readdata_File(const char* name);
int result();
void calculate();
int insertLine(int x1, int y1, int x2, int y2, char type);//0插入,非0出错
int deleteLine(int x1, int y1, int x2, int y2, char type);//0删除 1出错
int insertCircle(int x, int y, int r);
int deleteCircle(int x, int y, int r);
vector<pair<double, double>> pullIntersect();
vector<vector<int>> pullgraph();
提供了以上接口,下面一个个说明。
1. clear()接口
其目的在于清空所有数据,当用户想重新计算交点时,使用此函数清空之前存入的几何体数据。
2. readdata()接口
用于从控制台读取数据,每次可以读n个数据。
3. calculate()接口
当用户输入完成后,使用此函数对数据进行计算,并将算出的交点保存。
4. result()接口
返回计算出的交点数目
5. insertLine()接口
这个接口用于满足需求中的“支持插入,删除”。调用此函数会向数据中插入一条直线(会检查是否合法),若返回0表示插入成功,非0表示数据不合法。
6. deleteLine()接口
这个接口为了满足需求中的"支持插入,删除",调用此函数时,若找到用户想要删除的直线,就删除它并且返回0,否则返回1表示未找到。
7. insertCircle()接口
这个接口用于满足需求中的“支持插入,删除”。调用此函数会向数据中插入一个圆(会检查是否合法),返回0表示插入成功,非0表示数据不合法。
8. deleteCircle()接口
这个接口是为了满足需求中的"支持插入,删除",调用此函数时,若找到用户想要删除的圆,就删除它并且返回0,否则返回1表示未找到。
9. pullIntersect()接口
此函数用于提供给前端的UI所有交点数据,使得UI可以根据这些坐标来绘制交点。设计此函数的目的是为了满足需求“支持求解现有几何对象交点并绘制”。
10. pullgraph()接口
此函数用于提供给前端的UI所有几何图形数据,使得UI可以根据这些数据来绘制图像。设计此函数的目的是为了满足需求“支持绘制现有几何对象。”。
11. readdata_File(const char* name)接口
用于从文件中读取数据。
3.模块接口的设计与实现过程(包括算法核心)
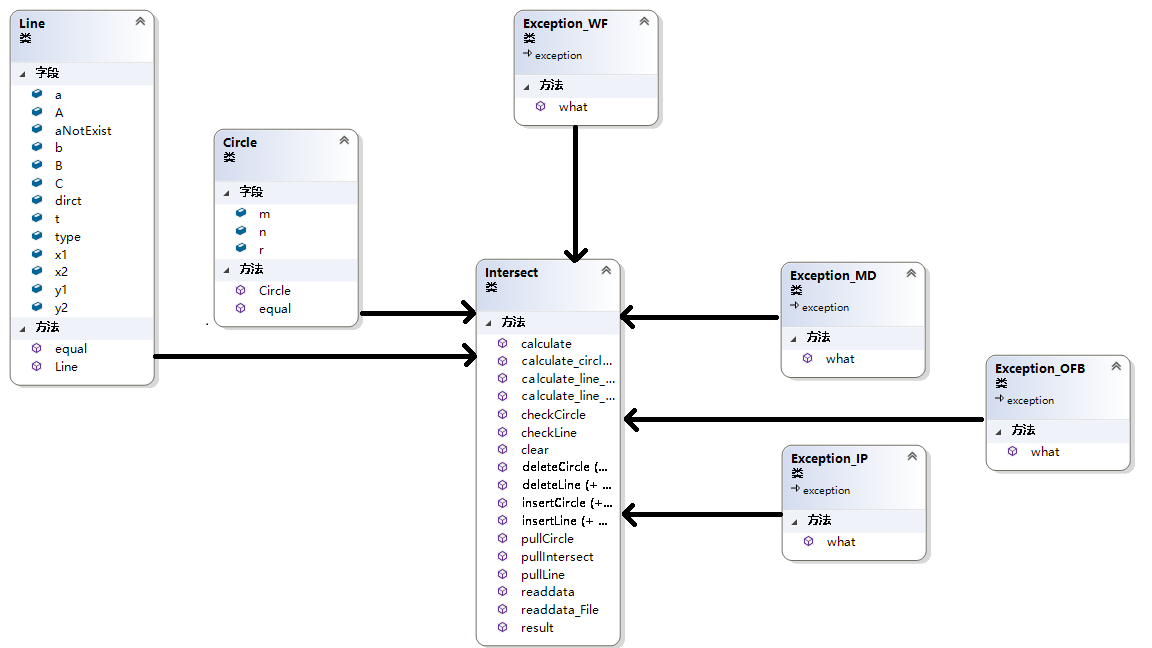
为了实现这些接口,我一共定义了三个类,Line类,circle类和Intersect类,Intersect负责最后的计算等等工作,而Line类和Circle类则是分别对线型和圆形的几何体进行处理,他们之间应该是一种关联的关系。
整个程序的设计大概有3个关键点,第一个是新加入的射线和线段的处理问题,这部分已在本文开头详细介绍;第二个关键是用户可能会有一些错误的数据插入,如何识别出这些问题并且报错,这里我的思路是错误有这么几种,第一种是在输入时的格式有问题,比如我应该输入L 0 0 1 1这样的格式表示一根直线,我少输入了一个数或者开头的L是别的符号等等,这种错误很好处理,在scanf_s时就可判断输入是否合法,第二种是虽然输入格式正确,但是这个参数的范围有问题,超过了极限值或者r小于0,这些错误可以在每次输入后通过if判断是否有问题,第三种则是最麻烦的,就是插入这个几何形后会出现无限多的交点,首先我们考虑圆和圆之间产生无限多交点,那么只有一种可能就是这两个圆是重合的,换句话说必须两个圆的圆心坐标一样且圆半径长一样,那么我们只需要在读入一个圆时与已经存入的所有圆比较,若是有一样的则报错,否则将这个圆加入set,其次是圆和线,必然不会有无限多交点,就不用考虑了,最后是线之间的无限多交点,首先任何线型要出现无限多交点他们必然是重合的,也就是说对于一个方程为\(Ax+By+C=0\)的线l1,和一个方程为\(ax+by+c=0\)的线l2,重合的必要条件是\(A*b=B*a\),且若是A!=0,那么\(A*c=C*a\);若是A==0,那么\(B*c=C*b\),其次我们还需要判断这两个线是否真的重合,如果其中一条是直线,那么一定重合,会有无限多个交点,如果没有一条是直线,那么如果两条都是射线,如果两条射线的方向一致,一定重合,如果方向相反,那么一条射线的顶点必须在另一条射线上才会重合,否则不会(这里注意如果只是顶点重合也不会造成无限交点的问题),如果是一条射线一条线段,那么线段的某一端点必须在射线上才会有无限交点问题,如果是两条线段,那么只要l1线段的左端点大于等于另l2线段的右端点,或者l1线段的右端点小于等于l2线段的左端点,就不会有问题,否则会出现无限交点的问题;最后一个关键是精度问题,这里没想出太好的解决方案,只是尽可能的减少了除法,开根号等运算的次数(比如求两直线交点用一般式而不是点斜式),这里也希望大佬提供好的思路。
四、UML类图
五、计算模块接口部分的性能改进
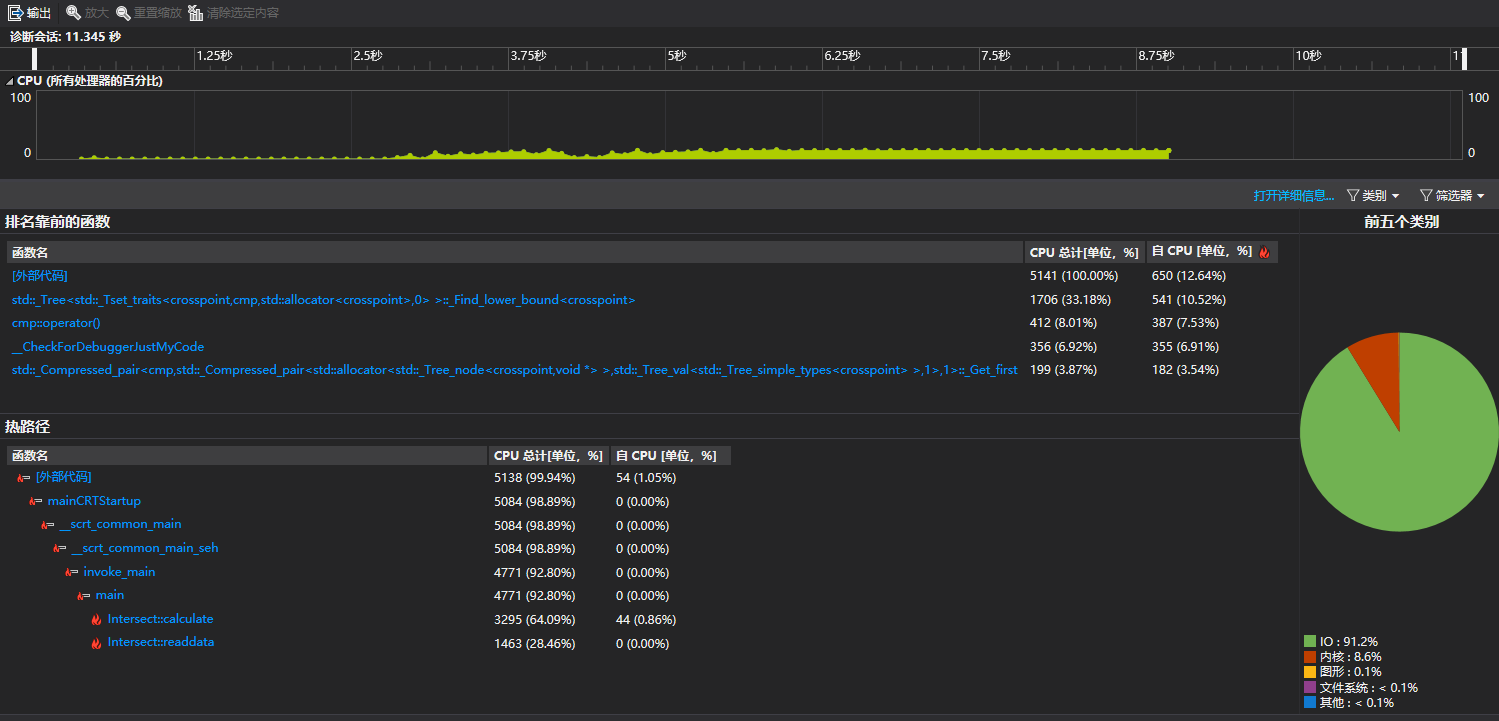
这是运行2000组数据的性能分析图,可以看到calculate()占用了64.09%的CPU时间,这是由于我们的算法采用暴力的做法,时间复杂度是O(n2),其次是readdata(),这是因为在读入数据时要检查数据的合法性,每读一个检查一次,每次检查是O(n)的时间复杂度,所以总共是O(n2)的时间复杂度。
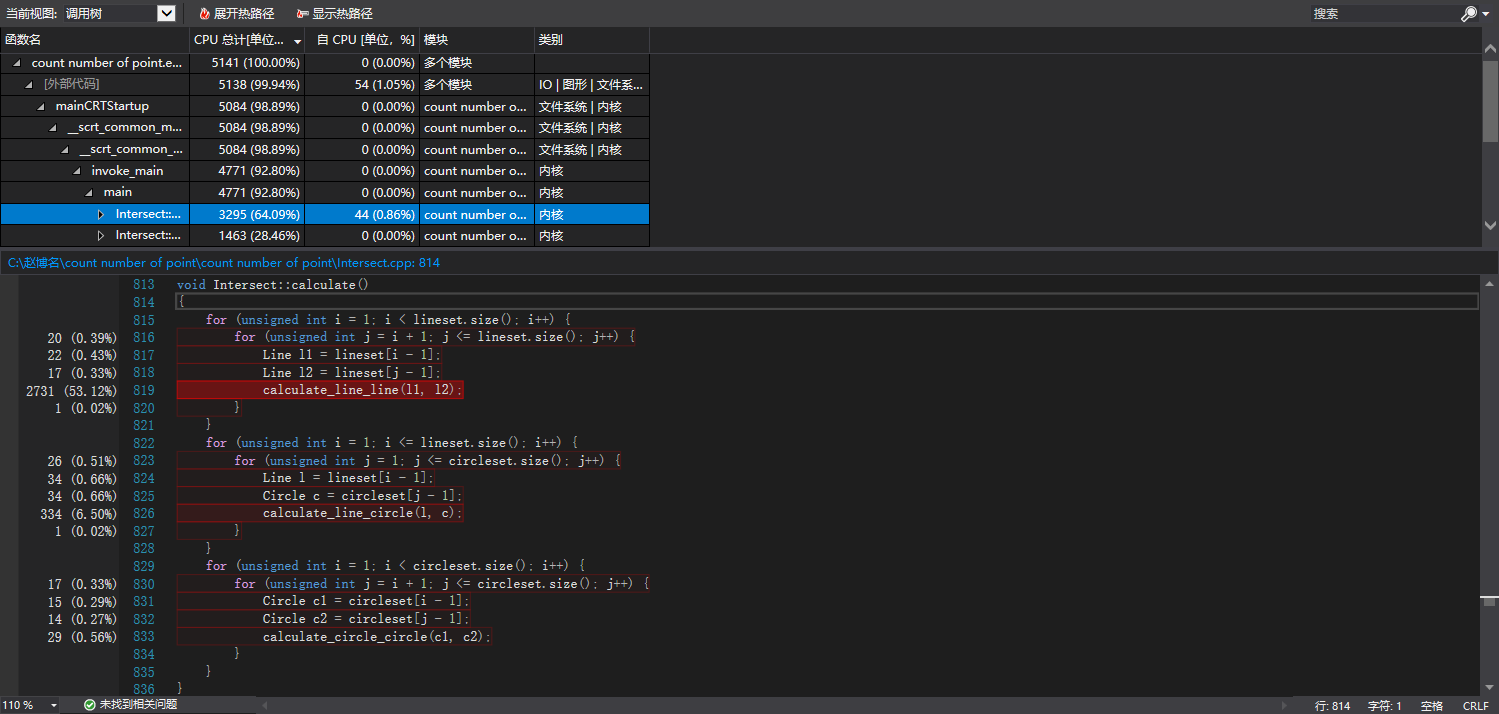
在这组数据中运行次数最多的是calculate_line_line(),这也符合我们之前的推测,由于第一次作业我们发现用set会比map稍微快一点,所以这次也是采用set存点的方法,因此想要改善这里的速度只能更换算法,所以并没有对程序进行太多性能上的优化。
六、看教科书和其它资料中关于 Information Hiding,Interface Design,Loose Coupling 的章节,说明你们在结对编程中是如何利用这些方法对接口进行设计的。
首先是Information Hiding,信息隐藏的意思是让模块仅仅公开必须要让外界知道的东西,而隐藏其他一切内容。在模块设计的接口设计中,就充分体现了信息隐藏这一原则——接口是模块的外部特征,应当公开;而数据结构、算法、实现体等则是模块的内部特征,应当隐藏。一个模块仅提供有限的接口,接口是模块与外界交互的惟一途径。这也是我设计的思路,封装成dll后public的只有接口,内部的具体实现,数据存在哪里都是隐藏的。
其次是接口设计。我认为一个好的接口设计应该有一下几个方面。一.接口的可读性,体现在给接口起名时能否让使用者大致明白这个接口是干什么的,在我的设计中,我全部采用英文全拼的方式,比如calculate,insertLine等等。二.接口的安全性,这一点我认为我基本上没有做到,唯一做的是消除了visual studio的警告信息(也算是一种安全?)。三.接口是否满足需求,这一点我在设计时,先把整个作业要求读了一遍,把core部分需要做的事一条条列下来,这样在写代码的时候会更有条理,提供的接口有逻辑,最关键的是在写完后和同伴交流,找到我们认为需要加入的接口以及没用的接口,再做调整。
最后是Loose Coupling,这一点体现在抛出异常时,若是我想修改异常的提示信息,我只需修改相应的异常类即可,而不用关心我的抛出异常的代码长什么样。但是这里我也有一些做的不好的地方,比如设计Line类和Circle类的时候,在其中对数据进行了特殊的处理,若是想要修改某一些参数,那么可能会导致整个代码重来。
七、计算模块部分单元测试展示
1.单元测试之新增功能
TEST_METHOD(calculate_line_line)
{
Intersect p;
Line l1(0, 0, 1, 1, 0);
Line l2(0, 0, 0, 1, 0);
int ret = p.calculate_line_line(l1, l2);
Assert::AreEqual(ret,(int)1);
Line l3(0, 0, 1, 1, 0);
Line l4(1, 0, 2, 1, 0);
ret = p.calculate_line_line(l3, l4);
Assert::AreEqual(ret, (int)0);
Line l5(0, 0, 1, 0, 2);
Line l6(1, 0, 2, 0, 2);
ret = p.calculate_line_line(l5, l6);
Assert::AreEqual(ret, (int)1);
Line l7(0, 0, 1, 0, 2);
Line l8(1, 1, 2, 0, 2);
ret = p.calculate_line_line(l7, l8);
Assert::AreEqual(ret, (int)0);
Line l9(0, 0, 1, 1, 1);
Line l10(0, 0, -1, -1, 1);
ret = p.calculate_line_line(l9, l10);
Assert::AreEqual(ret, (int)1);
Line l11(0, 0, 1, 0, 1);
Line l12(0, 1, 0, 2, 1);
ret = p.calculate_line_line(l11, l12);
Assert::AreEqual(ret, (int)0);
}
这是测试calculate_line_line函数的单元测试,考虑了直线,射线,线段的组合情况,考虑两线平行的情况,特殊的是比如两射线不平行,但求出的交点不在射线上,也无交点的情况。
TEST_METHOD(calculate_line_circle)
{
Intersect p;
Line l1(0, 0, 1, 1, 0);
Circle c1(0, 1, 1);
int ret = p.calculate_line_circle(l1, c1);
Assert::AreEqual(ret, (int)2);
Line l2(0, 0, 0, 1, 0);
Circle c2(1, 0, 1);
ret = p.calculate_line_circle(l2, c2);
Assert::AreEqual(ret, (int)1);
Line l3(0, 0, 1, 0, 0);
Circle c3(0, 2, 1);
ret = p.calculate_line_circle(l3, c3);
Assert::AreEqual(ret, (int)0);
Line l4(0, 1, 1, 1, 1);
ret = p.calculate_line_circle(l4, c1);
Assert::AreEqual(ret, (int)1);
Line l5(0, 0, 0, 1, 2);
Circle c4(0, 0, 3);
ret = p.calculate_line_circle(l5, c4);
Assert::AreEqual(ret, (int)0);
Line l6(2, 1, 0, 1, 2);
ret = p.calculate_line_circle(l4, c1);
Assert::AreEqual(ret, (int)1);
}
这是测试calculate_line_circle函数的单元测试,考虑了直线,射线,线段和圆交点的可能,其中直线考虑了和圆有一个,两个,无交点的三种情况,而射线和线段其实和直线的区别只是求出的交点可能不在线上,因此又单独测试了虽然可以通过方程求出交点,但不在线上的情况。
TEST_METHOD(calculate_circle_circle)
{
Intersect cal;
Circle c1(0, 0, 1);
Circle c2(1, 1, 1);
int ret = cal.calculate_circle_circle(c1, c2);
Assert::AreEqual(ret, (int)2);
Circle c3(0, 0, 2);
Circle c4(3, 0, 1);
ret = cal.calculate_circle_circle(c3, c4);
Assert::AreEqual(ret, (int)1);
Circle c5(0, 0, 3);
Circle c6(0, 0, 1);
ret = cal.calculate_circle_circle(c5, c6);
Assert::AreEqual(ret, (int)0);
Circle c7(0, 0, 1);
Circle c8(0, 9, 1);
ret = cal.calculate_circle_circle(c7, c8);
Assert::AreEqual(ret, (int)0);
}
这是测试calculate_circle_circle函数的单元测试,考虑了两个圆有2个,1个,0个交点的情况,同时还考虑了一个圆在另一个圆内部的情况

可以看到测试通过。
2.单元测试之接口部分
从难度上看,clear()接口,pullgraph()接口,result()接口,pullintersect()接口都是不需要测试的,因为他们单纯的返回一个数据结构或者是一个简单的初始化过程,而calculate(),readdata()等接口均是从上一次的个人作业中沿用下来的,已进行过测试,因此我们在这里主要测试新增的4个接口
TEST_METHOD(deleteline)
{
Intersect p;
int ret;
p.insertLine(0, 0, 1, 1, 'L');
p.insertLine(0, 0, 0, 1, 'R');
p.insertLine(0, 0, 1, 0, 'S');
ret = p.deleteLine(1, 1, 2, 2, 'R');
Assert::AreEqual(ret, (int)1);
ret = p.deleteLine(1, 1, 2, 2, 'L');
Assert::AreEqual(ret, (int)0);
ret = p.deleteLine(0, 0, 1, 1, 'L');
Assert::AreEqual(ret, (int)1);
ret = p.deleteLine(0, 0, 0, -1, 'R');
Assert::AreEqual(ret, (int)1);
ret = p.deleteLine(0, 0, 1, 2, 'S');
Assert::AreEqual(ret, (int)1);
}
这是测试deleteline()接口的单元测试,在这里我设计数据时考虑的主要是即使两线重合了,他们也不是同一条线,不能删除的情况,例如第一个点,两线重合,但一个是直线,一个是射线,故不能删除,返回1表示出错;第二个点是两直线重合的情况,需要删除,返回0;第三个点是一个测试删除成功的点,因为第二个点已经删除了这条直线,第三个点再次请求删除这条直线时应该找不到这条直线了,故返回1;第四个点是测试两射线重合时的情况,两射线重合并且端点相同,但是射线的方向不相同,应当返回1;最后一个测试点时测试两线段的情况,如果两线段一个端点相同另一个不相同,肯定不是同一条线段,应当返回1。
TEST_METHOD(deletecircle)
{
Intersect p;
p.insertCircle(0, 0, 1);
p.insertCircle(1, 1, 1);
p.insertCircle(0, 0, 2);
int ret = p.deleteCircle(1, 1, 1);
Assert::AreEqual(ret, (int)0);
ret = p.deleteCircle(1, 1, 1);
Assert::AreEqual(ret, (int)1);
ret = p.deleteCircle(0, 0, 1);
Assert::AreEqual(ret, (int)0);
ret = p.deleteCircle(0, 2, 1);
Assert::AreEqual(ret, (int)1);
}
这是测试deletecircle()接口的单元测试,在这里我主要考虑的特殊点是删除了一个圆后,再次删除这个圆,应当报错,以及两个圆相同的判定必须是圆心相等且半径相同。测试比较简单,不赘述。
TEST_METHOD(insertLine)
{
Intersect p;
int ret = p.insertLine(1, 2, 1, 2, 'L');
Assert::AreEqual(ret, (int)1);
ret = p.insertLine(100001, 0, 2, 1, 'L');
Assert::AreEqual(ret, (int)2);
ret = p.insertLine(0, -100006, 2, 1, 'L');
Assert::AreEqual(ret, (int)3);
p.insertLine(0, 0, 1, 2, 'L');
ret = p.insertLine(0, 0, -1, -2, 'R');
Assert::AreEqual(ret, (int)4);
ret = p.insertLine(0, 0, 1, 5, 'C');
Assert::AreEqual(ret, (int)5);
ret = p.insertLine(0, 0, 1, 1, 'L');
Assert::AreEqual(ret, (int)0);
}
这是测试insertLine()接口的单元测试。在这里我主要考虑的是插入一个坐标值超过限定的线,插入一个type不符合线标准的值,插入一个两顶点重复的线,插入一个会产生无数交点的线,以及一个可以正常插入的线,这样就考虑到了所有可能异常的情况。
TEST_METHOD(insertCircle)
{
Intersect p;
int ret = p.insertCircle(0, 0, 100005);
Assert::AreEqual(ret, (int)1);
ret = p.insertCircle(-100008, 2, 4);
Assert::AreEqual(ret, (int)2);
ret = p.insertCircle(0, 2, -2);
Assert::AreEqual(ret, (int)3);
p.insertCircle(0, 0, 1);
ret = p.insertCircle(0, 1, 1);
Assert::AreEqual(ret, (int)0);
ret = p.insertCircle(0, 0, 1);
Assert::AreEqual(ret, (int)4);
}
这是测试insertcircle()接口的单元测试。在这里我主要考虑的是是插入一个坐标值超过限定的圆,插入一个半径是负数的圆,插入一个会产生无数交点的圆,以及一个可以正常插入的线,这样就考虑到了所有可能异常的情况。
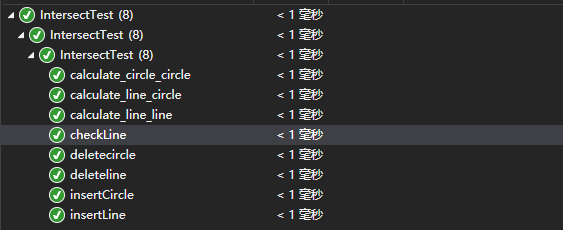
3.所有单元测试覆盖率
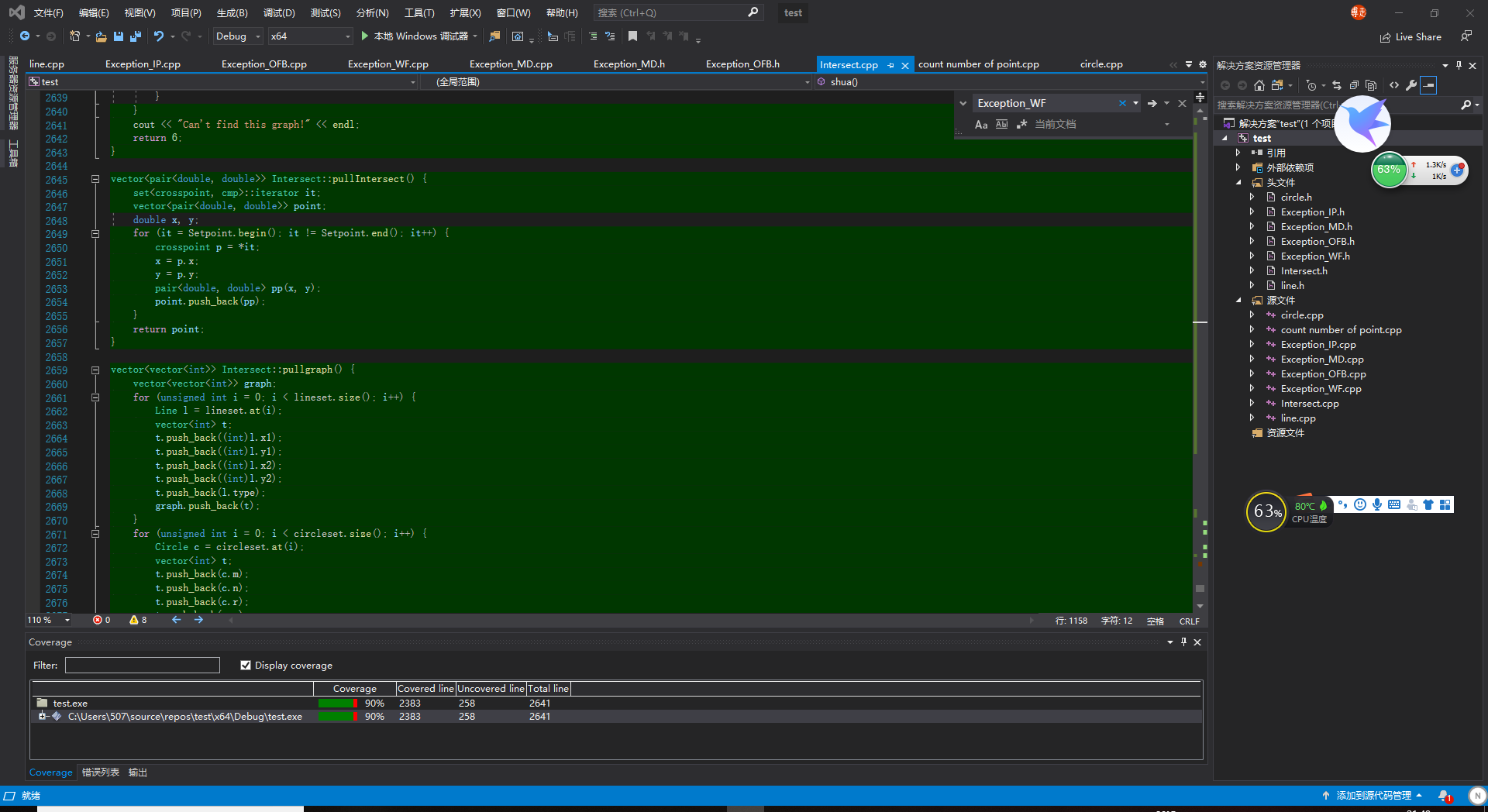
这是使用OpenCppCoverage测试的覆盖率结果。
八、计算模块部分异常处理说明
1.支持的异常
| 异常 | 描述 |
|---|---|
| Exception_OFB | 越界异常,在输入几何体的参数时,如果超出了设定的范围(-100000,100000),或者圆的半径小于0,就会抛出这个异常。 |
| Exception_IP | 无限交点异常,当新增一个几何体后,所求交点数目变成无限多个,则会抛出这个异常 |
| Exception_WF | 错误格式异常,当输入几何体数据的格式不符合预定格式时,则抛出这个异常 |
| Exception_MD | 无效定义异常,当输入的线型几何体的两点坐标相同时,认为这条线是无效的,抛出此异常 |
| 异常 | 目标 |
|---|---|
| Exception_OFB | 提醒用户输入的参数范围应该在什么区间内,并且返回到输入处继续输入 |
| Exception_IP | 提醒用户加入的这个几何体是禁止的,并返回到输入界面重新输入 |
| Exception_WF | 提示用户标准的输入格式,并返回到输入界面继续输入 |
| Exception_MD | 提示用户两个点的坐标必须不同,并返回到输入界面继续输入 |
2.单元测试之异常
我们通过insertLine()函数的测试来测试我们是否正确的抛出异常,因为在每一种异常被抛出后,我们的代码会catch到这个异常,并且return不同的数值,因此利用这一点可以很好地进行单元测试。
TEST_METHOD(insertLine)
{
Intersect p;
int ret = p.insertLine(1, 2, 1, 2, 'L');
Assert::AreEqual(ret, (int)1);
ret = p.insertLine(100001, 0, 2, 1, 'L');
Assert::AreEqual(ret, (int)2);
ret = p.insertLine(0, -100006, 2, 1, 'L');
Assert::AreEqual(ret, (int)3);
p.insertLine(0, 0, 1, 2, 'L');
ret = p.insertLine(0, 0, -1, -2, 'R');
Assert::AreEqual(ret, (int)4);
ret = p.insertLine(0, 0, 1, 5, 'C');
Assert::AreEqual(ret, (int)5);
ret = p.insertLine(0, 0, 1, 1, 'L');
Assert::AreEqual(ret, (int)0);
}
返回5说明抛出了Exception_WF,返回1说明抛出了Exception_MD,返回2和3说明抛出了Exception_OFB的两种不同格式的异常,返回4说明抛出了Exception_IP,返回0说明这条线是合法的。
通过这个测试,可以发现异常能被正确的抛出且捕获。
九、界面模块的详细设计过程
本着简介明了的设计思路,我设计了两个窗口,一个是图形操作界面,一个是作图界面。
图形操作界面
图形操作界面使用网格布局(gridlayout),界面中有两个列表,两个文本框,五个按钮。左边的列表是存储已有的几何对象,右边的列表是记录当前几何对象的交点。左边的文本框用来输入标准形式的几何图形,add graph按钮将输入的图形加入列表,delete graph按钮将选中的几何图形删除。右边的文本框用来输入需要导入几何对象的txt文件名(全名 xxx.txt),input text按钮确认导入的文件名,draw graph按钮绘制当前列表中的几何图形,draw intersect按钮绘制当前列表中的几何图形并求解交点。
ListWindow::ListWindow(QWidget* parent) :
QDialog(parent) {
QGridLayout* gridLayout = new QGridLayout();
gridLayout->addWidget(textlable1 = new QLabel("Graphs:"), 0, 0, 1, 1);
gridLayout->addWidget(textlable2 = new QLabel("Input Graph here:"), 0, 1, 1, 1);
gridLayout->addWidget(textlable3 = new QLabel("Input text name here:"), 0, 2, 1, 1);
gridLayout->addWidget(textlable4 = new QLabel("Intersects:"), 0, 3, 1, 1);
gridLayout->addWidget(leftList = new QListWidget(), 1, 0, 6, 1);
gridLayout->addWidget(rightList = new QListWidget(), 1, 3, 6, 1);
gridLayout->addWidget(textInput = new QLineEdit(), 1, 1, 1, 1);
gridLayout->addWidget(add = new QPushButton("add graph"), 2, 1, 1, 1);
gridLayout->addWidget(deleteButton = new QPushButton("delete graph"), 3, 1, 1, 1);
gridLayout->addWidget(inputText = new QLineEdit(), 1, 2, 1, 1);
gridLayout->addWidget(inputButton = new QPushButton("input text"), 2, 2, 1, 1);
gridLayout->addWidget(drawgraph = new QPushButton("draw graph"), 3, 2, 1, 1);
gridLayout->addWidget(getIntesect = new QPushButton("draw intersect"), 4, 2, 1, 1);
QObject::connect(add, SIGNAL(clicked()), this, SLOT(addGraph()));
QObject::connect(deleteButton, SIGNAL(clicked()), this, SLOT(deleteGraph()));
QObject::connect(inputButton, SIGNAL(clicked()), this, SLOT(getText()));
QObject::connect(getIntesect, SIGNAL(clicked()), this, SLOT(calculate()));
QObject::connect(drawgraph, SIGNAL(clicked()), this, SLOT(drawGraph()));
QStringList items;
leftList->addItems(items);
this->setLayout(gridLayout);
}
作图界面

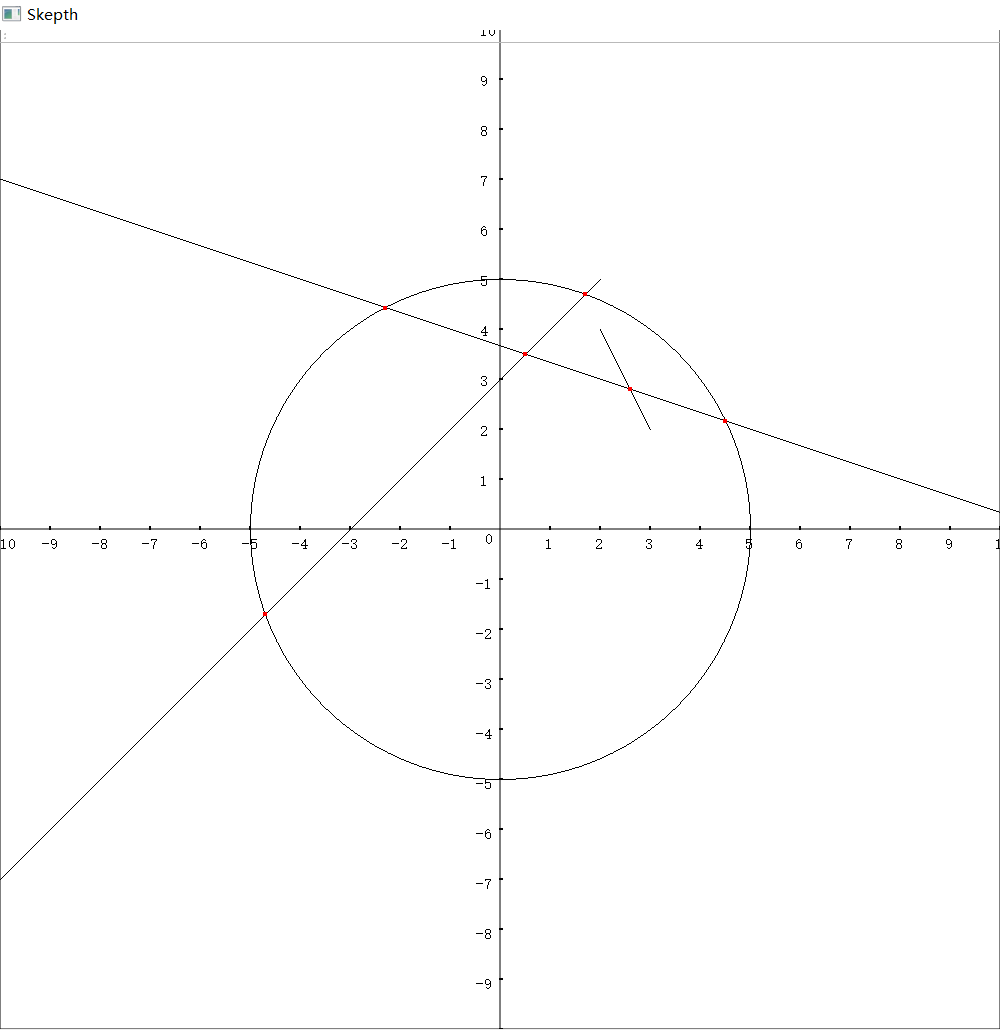
构建一个直角坐标系,图形用黑色细线画出,交点用红点标出。
Skepth::Skepth(QWidget *parent)
: QMainWindow(parent)
{
ui.setupUi(this);
image = QImage(1000, 1000, QImage::Format_RGB32);
QColor backColor = qRgb(255, 255, 255);
image.fill(backColor);
Paint();
}
void Skepth::Paint() {
QPainter painter(&image);
painter.setRenderHint(QPainter::Antialiasing, true);//设置反锯齿模式,好看一点
pointx = 500;
pointy = 500;//确定坐标轴起点坐标,这里定义(500,500)
width = 1000 - pointx;
height = 1000 - pointy;//确定坐标轴宽度跟高度 上文定义画布为1000X1000,宽高依此而定。
//绘制坐标轴 坐标轴原点(500,500)
painter.drawRect(0, 0, 1000, 1000);//外围的矩形,从(0,0)起,到(1000,1000)结束,周围留了5的间隙。
painter.drawLine(-5, pointy, 1005, pointy);//坐标轴x宽度为width
painter.drawLine(pointx, -5, pointx, 1005);//坐标轴y高度为height
}
十、界面模块与计算模块的对接
要求的UI模块需要有4个基础功能
- 支持从文件导入几何对象的描述。
- 支持几何对象的添加、删除。
- 支持绘制现有几何对象。
- 支持求解现有几何对象交点并绘制。
支持从文件中导入集合对象的描述
由于在core中已经有了从文件中读取数据的接口
void readdata_File(const char* name);
UI只需要获取待读入文件的文件名,再使用接口即可。同时需要在core读取几何图形时更新GraphList。
void ListWindow::getText() {
QString text = inputText->text();
p.readdata_File(text.toStdString().c_str());
leftList->clear();
vector<vector<int>> temp = p.pullgraph();
int i, x1, x2, y1, y2, type;
for (i = 0; i < temp.size(); i++) {
x1 = temp[i][0];
y1 = temp[i][1];
x2 = temp[i][2];
y2 = temp[i][3];
type = temp[i][4];
string graphType, str;
if (type == 0) {
graphType = "L ";
}
else if (type == 1) {
graphType = "R ";
}
else if (type == 2) {
graphType = "S ";
}
else if (type == 3) {
graphType = "C ";
}
if (type == 0 || type == 1 || type == 2) {
str = graphType + to_string(x1) + " " + to_string(y1) + " " + to_string(x2) + " " + to_string(y2);
}
else if (type == 3) {
str = graphType + to_string(x1) + " " + to_string(y1) + " " + to_string(x2);
}
text = QString::fromStdString(str);
leftList->addItem(text);
}
}
支持对集合对象的添加、删除
在core中有相应的添加删除操作
int insertgraph(string s);
int deletegraph(string s);
UI只需要将需要添加或删除的对象通过接口传递给core,同时在core增删集合图形时更改Graph List。
void ListWindow::addGraph() {
QString text = textInput->text();
int sigh = p.insertgraph(text.toStdString().c_str());
if (sigh == 0) {
leftList->addItem(text);
textInput->clear();
}
}
void ListWindow::deleteGraph() {
QList<QListWidgetItem*> list = leftList->selectedItems();
if (list.size() == 0) {
return;
}
QListWidgetItem* sel = list[0];
string item = sel->text().toStdString().c_str();
int sigh = p.deletegraph(item);
if (sigh == 0)
{
int r = leftList->row(sel);
leftList->takeItem(r);
}
}
支持绘制现有几何图像
现有的几何图像存储在core之中,需要通过
vector<vector<int>> pullgraph();
接口来获得一个graph Set。每个graph包含5个参数,type,< x1, y1>, <x2, y2>,type是图形种类的标号直线,射线,线段,圆分别用0,1,2,3来表示,如果图形是圆时,<x2,y2>所表示的是<r,r>。由于图形的比例跨度过大,我们需要先确定能够绘制最大的图形,所以要先遍历所有图形,确定下直角坐标系的比例尺,接下来只需要在直角坐标系中逐一画出图形,最后再标识刻度尺。
void Skepth::getGraph(vector<vector<int>> temp) {
int i, j;
int x1, y1, x2, y2, type;
max = getMax(temp);
double cap = 500.0 / max;
for (i = 0; i < temp.size(); i++) {
x1 = temp[i][0];
y1 = temp[i][1];
x2 = temp[i][2];
y2 = temp[i][3];
type = temp[i][4];
if (type == 0 || type == 1 || type == 2) {
drawAline(x1, y1, x2, y2, type, cap);
}
else if (type == 3) {
drawCylcle(x1, y1, x2, cap);
}
}
}
void Skepth::scalePaint() {
//int max = 10;
QPainter painter(&image);
QPen penDegree;
penDegree.setColor(Qt::black);
penDegree.setWidth(2);
painter.setPen(penDegree);
//画上x轴刻度线
painter.drawText(pointx - 15, pointy + 15, QString::number(int(0)));
for (int i = 0; i < 10; i++)//分成10份
{
//选取合适的坐标,绘制一段长度为4的直线,用于表示刻度
painter.drawLine(pointx + (i + 1) * width / 10, pointy, pointx + (i + 1) * width / 10, pointy - 2);
painter.drawText(pointx + (i + 1) * width / 10 - 5, pointy + 20, QString::number((int)((i + 1) * ((double)max / 10))));
painter.drawLine(pointx - (i + 1) * width / 10, pointy, pointx - (i + 1) * width / 10, pointy - 2);
painter.drawText(pointx - (i + 1) * width / 10 - 8, pointy + 20, QString::number((int)(-(i + 1) * ((double)max / 10))));
}
//y轴刻度线
double _maStep = (double)max / 10;//y轴刻度间隔需根据最大值来表示
for (int i = 0; i < 10; i++)
{
//主要就是确定一个位置,然后画一条短短的直线表示刻度。
painter.drawLine(pointx, pointy - (i + 1) * height / 10, pointx + 2, pointy - (i + 1) * height / 10);
painter.drawText(pointx - 20, pointy - (i + 0.85) * height / 10, QString::number((int)(_maStep * (i + 1))));
painter.drawLine(pointx, pointy + (i + 1) * height / 10, pointx + 2, pointy + (i + 1) * height / 10);
painter.drawText(pointx - 24, pointy + (i + 1.2) * height / 10, QString::number((int)(-_maStep * (i + 1))));
}
}
支持求解现有几何对象的交点并绘制
现有几何对象的交点存储在core中,需要通过
vector<pair<double, double>> pullIntersect();
接口来获得一个Point Set。每个Point有两个参数<x1,y1>,只需要遍历Point set并逐一将其画出并添加到右端的Intersect Set。
void ListWindow::calculate() {
p.calculate();
Skepth *w = new Skepth;
w->show();
w->getGraph(p.pullgraph());
w->getIntersect(p.pullIntersect());
rightList->clear();
vector<pair<double, double>> intersectList = p.pullIntersect();
for (int i = 0; i < intersectList.size(); i++) {
string point = "<" + to_string(intersectList[i].first) + "," + to_string(intersectList[i].second) + ">";
rightList->addItem(QString::fromStdString(point));
}
w->scalePaint();
}
功能演示
添加几何图形
从文件导入图形
删除图形

绘制几何图形
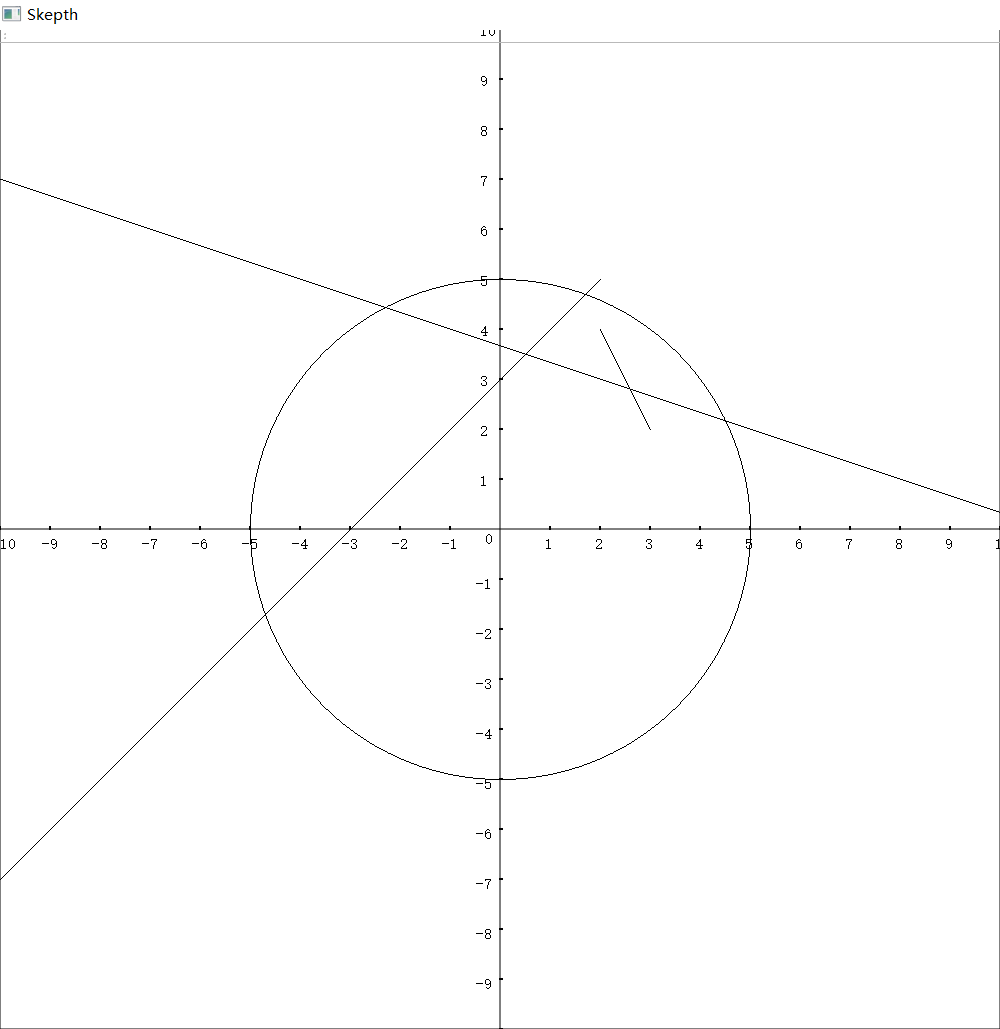
绘制交点
十一、描述结对的过程
我们采用腾讯会议作为交流的平台,一个人在写的时候另一个人可以通过屏幕共享看到并时刻交流
十二、结对编程的优缺点
| 优点 | 描述 |
|---|---|
| 互相监督,无法偷懒摸鱼 | 两个人互相监督互相配合,如果一个人偷懒那么另一个人会发现并去提醒他,可以保证工作的进度。 |
| 互相学习 | 两个人各有擅长所在,有的人可能擅长算法,有的人擅长UI的设计与编写,这样在结对编程时可以互相学习一些技巧。 |
| 互相帮助,渡过难关 | 当在处理某个问题时卡住了,两个人可以讨论,一起上网找资料,互相鼓励,更快的渡过难关。 |
| 一人写一人看减少bug | 一人在写一人看,可以降低出错的概率,减少bug。 |
| 缺点 | 描述 |
|---|---|
| 容易内耗 | 两人就一个问题产生了意见的分歧,都想说服对方用自己的方法,无谓的降低效率。 |
| 降低了开发的速度 | 如果两人不是一人写一人看的模式,每天会多出一倍的工作时间,比如讲任务分为前端和后端,一人负责一部分,会比结对更快的完成任务。 |
| 容易在工作时聊天 | 两个人连着麦写代码,写了一会儿突然发起一个话题,无休止的聊了下去,降低工作效率。 |
| 对于性格不和的人会产生争执 | 一个人喜欢敏锐开发,每天工作8小时,另一个人喜欢多干几天,每天工作3小时,这两个人结对会造成就工作时长的争执,团队不和无法继续工作。 |
我的优点是:认真负责,对自己的工作要做到位;效率较高;善于从网上学习资料 缺点是:不能做到精益求精,感觉满足需求了,到位了,就不想优化了。
同伴的优点是:分工能力强;同样的认真负责,效率高;能很好地提供思路,指出问题所在;乐于助人;编程能力强,能攻克一些难关 缺点是:不能一次指出所有问题(hhh这样改起代码有时需回退版本)。



