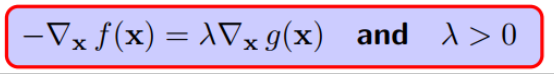广义拉格朗日与对偶问题

广义拉格朗日函数

给定不等式约束问题

\[\min_{z \in \mathbb{R}^{n}} f(x) \]

\[\begin{array}{l} {\text { s.t. } \ c_{i}(x) \le 0, \quad i=1,2, \cdots, k} \\ {\quad \ \ \ \ h_{j}(x)=0, \quad j=1,2, \cdots, l}\end{array} \]

定义广义拉格朗日函数(generalized Lagrange function)

\[L(x, \alpha, \beta)=f(x)+\sum_{i=1}^{k} \alpha_{i} c_{i}(x)+\sum_{j=1}^{l} \beta_{j} h_{j}(x) \]

这里\(x=\left(x^{(1)}, x^{(2)}, \cdots, x^{(n)}\right)^{\mathrm{T}} \in \mathbb{R}^{n}, \ \alpha_{i}, {\beta}_{j}\)是拉格朗日乘子，\(\alpha_i\ge 0\), 考虑\(x\)的函数

\[\theta_{P}(x)=\max _{\alpha, \beta; \alpha_{i} \ge 0} L(x, \alpha, \beta) \]

则

\[\theta_{p}(x)=\left\{\begin{array}{l}{f(x)}, \ x\mbox{满足原始问题约束} \\ {+\infty}, \ \mbox{其他}\end{array}\right. \]

（有严格证明，这里略过）

极小化问题\(\min _{x} \theta_{P}(x)=\min _{x} \max _{\alpha, \beta ; \alpha_{i} \ge0} L(x, \alpha, \beta)\)原问题有相同的解

拉格朗日函数相当于构造了一个含参函数，在满足约束条件的情况下，这个函数的值总是小于等于目标函数\(f(x)\)。而我们此时选取合适的参数\(α\)、\(β\)令该函数最大可使等号成立，即令\(L(x,α,β)=f(x)\)；若不满足约束条件，则总存在\(α、β\)使得该函数趋向于+∞。

定义原始问题的最优值为\(p^{*}=\min _{x} \theta_{p}(x)\)

对偶问题

定义\(\theta_{D}(\alpha, \beta)=\min _{x} L(x, \alpha, \beta)\)

我们得到极大极小问题

\[{\max _{\alpha, \beta} \theta_{D}(\alpha, \beta)=\max _{\alpha, \beta} \min _{x} L(x, \alpha, \beta)} \\ {\text { s.t. } \quad \alpha_{i} \geq 0, \quad i=1,2, \cdots, k} \]

称为原问题（极小极大问题）的对偶问题

定义对偶问题的最优值为\(d^{*}=\max _{\alpha, \beta ; \alpha_{i} \geq 0} \theta_{D}(\alpha, \beta)\)

原始问题与对偶问题的关系

性质1 （弱对偶性）\(d^* \le p^*\)。p是先求最大的一块区域然后在这块区域求最小，d是先求最小的一块区域然后在这块区域求最大，最大里面的最小，总会比最小里面的最大要大。

性质2 （强对偶充分条件）若\(f(x)\)和\(c_i(x)\)是凸函数，\(h_j(x)\)是仿射函数，并且不等式约束是严格可行的（即\(\exists x,\forall i,\text{有}c_i(x)<0\)）则存在\(x^*\),\(\alpha^*\) ,\(\beta^*\) 使\(x^*\)是原始问题的解，\(\alpha^*,\beta^*\)是对偶问题的解， 并且

\[p^{*}=d^{*}=L\left(x^{*}, \alpha^{*}, \beta^{*}\right) \]

性质3 （强对偶充要条件）若\(f(x)\)和\(c_i(x)\)是凸函数，\(h_j(x)\)是仿射函数，并且不等式约束是严格可行的，则\(x^*\)是原始问题的解，\(\alpha^*,\beta^*\)是对偶问题的解的充要条件就是它们满足KKT（ Karush-Kuhn-Tucker）条件

\[\begin{array}{l}{\nabla_{x} L\left(x^{*}, \alpha^{*}, \beta^{*}\right)=0} \\ {\nabla_{\alpha} L\left(x^{*}, \alpha^{*}, \beta^{*}\right)=0} \\ {\nabla_{\beta} L\left(x^{*}, \alpha^{*}, \beta^{*}\right)=0}\end{array}\\ \begin{array}{rl}{\alpha_{i}^{*} c_{i}\left(x^{*}\right)=0,} & {i=1,2, \cdots, k} \\ {c_{i}\left(x^{*}\right) \le0,} & {i=1,2, \cdots, k} \\ {\alpha_{i}^{*} \ge 0,} & {i=1,2, \cdots, k} \\ {h_{j}\left(x^{*}\right)=0,} & {j=1,2, \cdots, l}\end{array} \]

KKT条件的直观理解(两个例子)

等式约束

目标函数\(f(x) = x_1 + x_2\)，等式约束\(h(x) = x_1^2 + x_2^2 - 2\) ，求解极小值点。

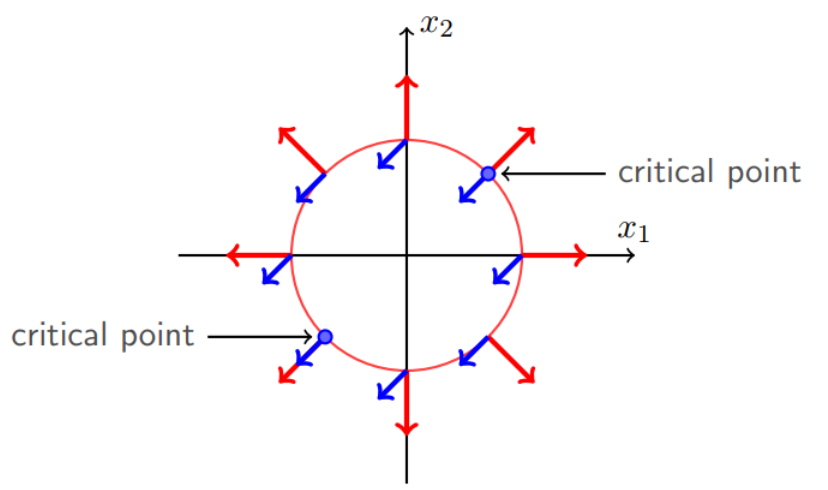
不等式约束

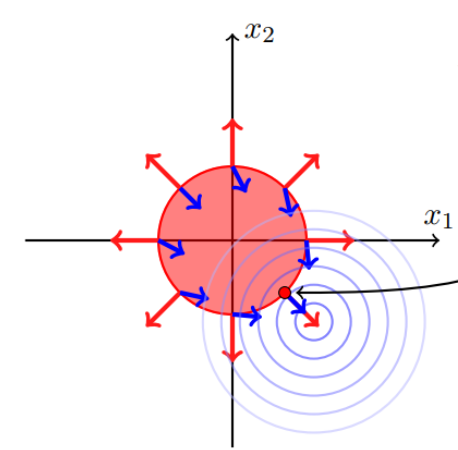
考虑目标函数\(f(x) = x_1^2 + x_2^2\) ，不等式约束\(g(x) = x_1^2 + x_2^2 - 1\le0\)，显然\(f(x)\)的极小值为原点(0,0)，落在可行域内。可行域以原点为圆心，半径为1。

这种情况约束不起作用，考虑极小值点\(x^*\)，这个时候，\(g(x^*) < 0\)，\(f(x^*)\)的梯度等于0。

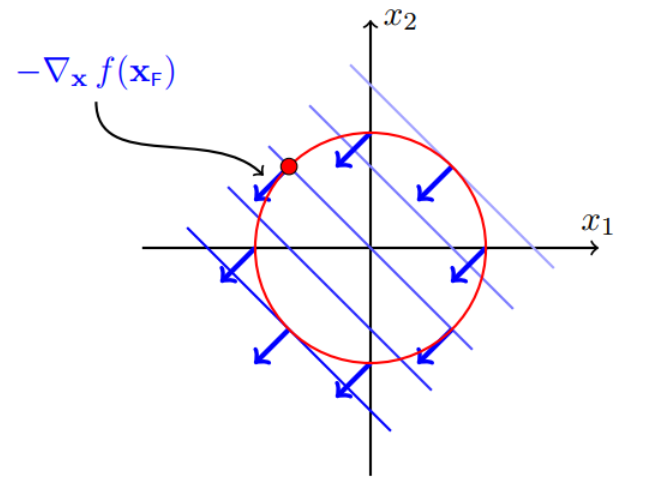
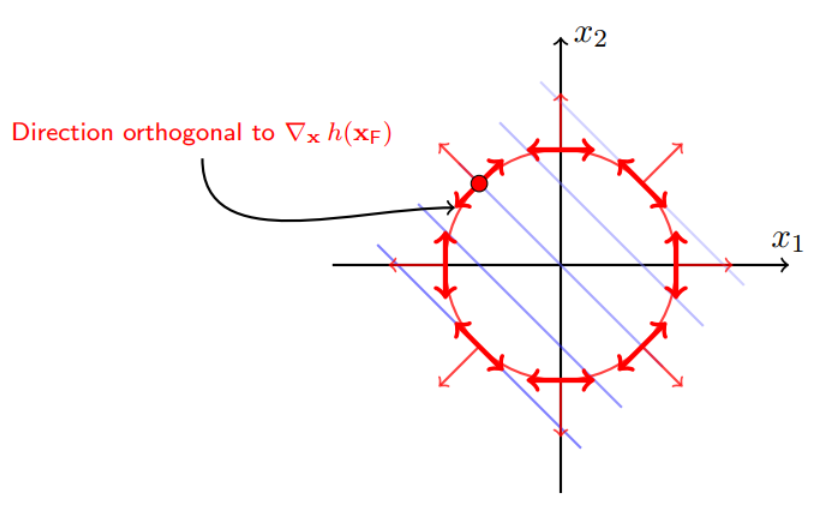
考虑目标函数\(f(x) = (x_1 - 1.1)^2 + (x_2 + 1.1)^2\) ，不等式约束\(g(x) = x_1^2 + x_2^2 - 1 \le0\)，显然f(x)的极小值为原点(1.1, -1.1)，落在可行域外。可行域以原点为圆心，半径为1。这种情况约束起作用，要考虑求解\(f(x)\)在可行域内的极小值点