0.PTA得分截图

1.本周学习总结
1.1 总结查找内容
顺序查找
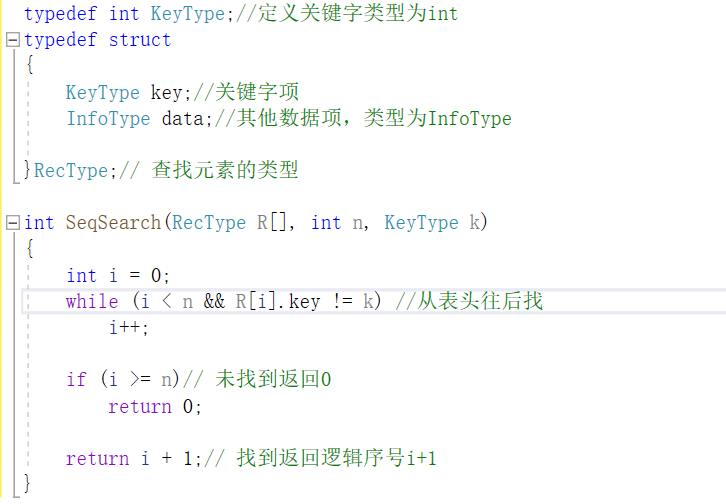
- 顺序查找是从表的一端到另一端逐个将元素关键字和定值k比较是否相等的算法。对无序线性表进行顺序查找,查找失败时要遍历整个线性表。
- 代码实现:
![]()
二分查找
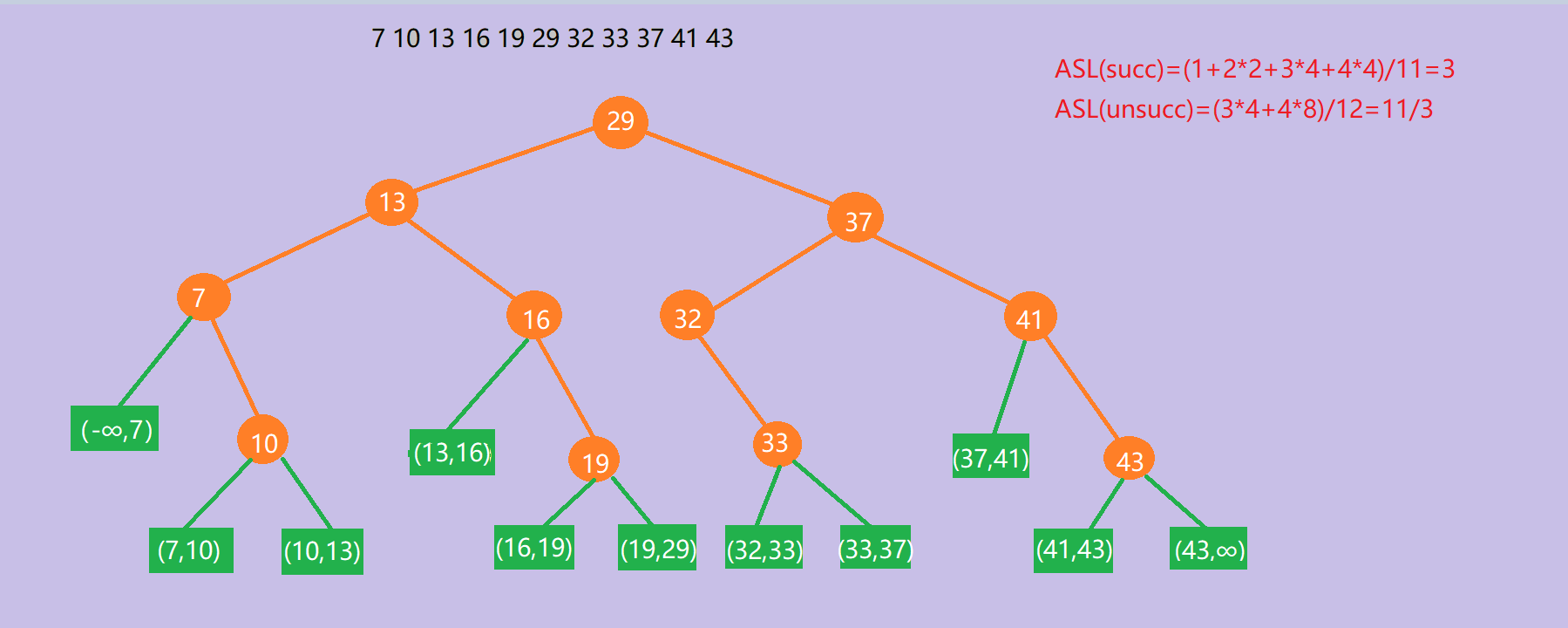
- 二分查找思路主要是将给定值key与表中中间位置元素的关键字比较,若相等,则返回该元素的位置;若不等,则在前半部分或者是后半部分进行查找。它仅适用于有序的顺序表
![]()
二叉搜索树
二叉搜索树创建

二叉搜索树的插入
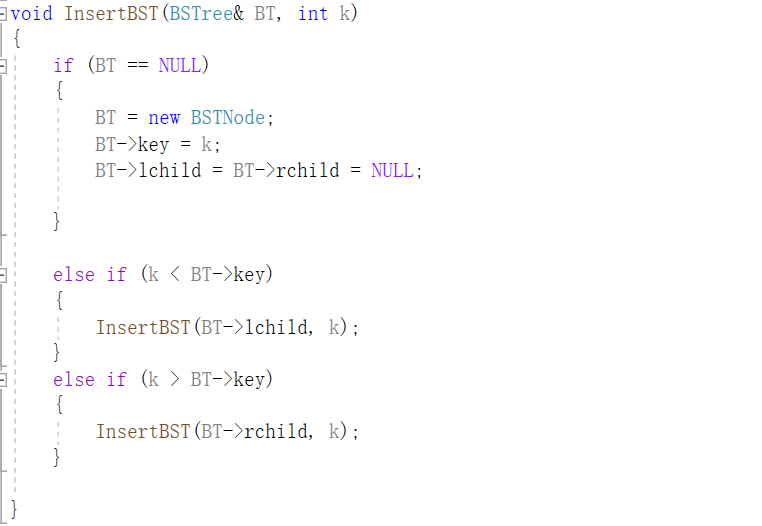
二叉搜索树的删除

AVL树
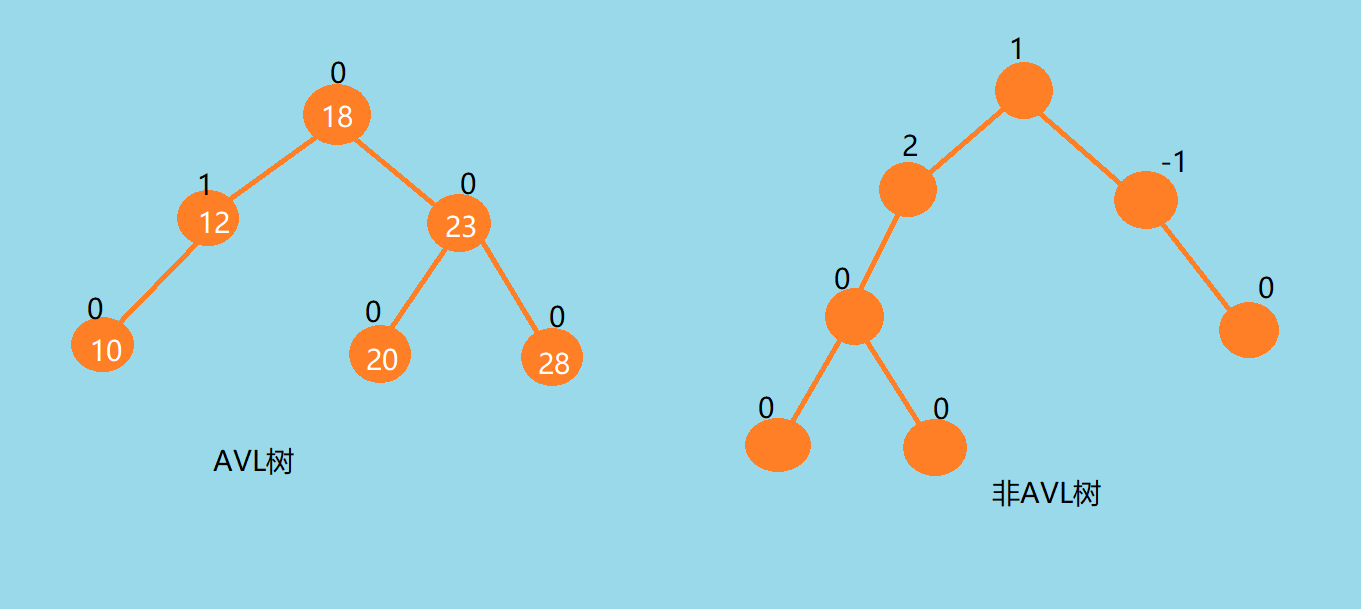
- 平衡二叉树(AVL树)是左右子树的高度之差绝对值不超过1的二叉搜索树,且其左右子树又是一棵平衡二叉树,即左右子树的高度差只能为-1,0,1。
![]()
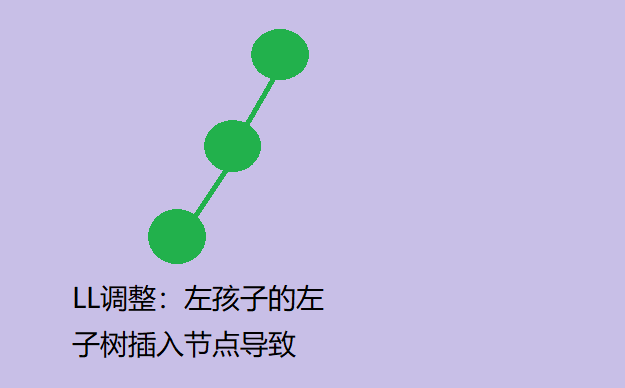
LL调整
-
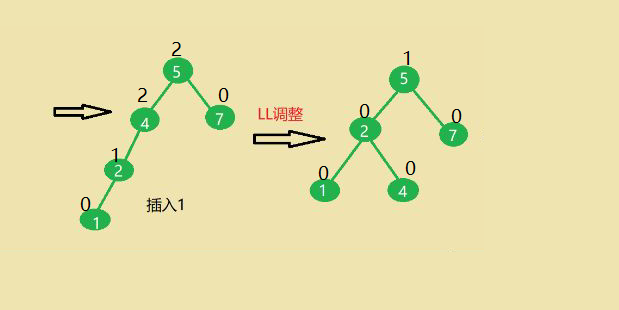
LL:某分支节点的左孩子的左子树插入节点引起失衡
![]()
-
插入1导致节点4失衡,进行LL调整,右旋使之平衡。
(1)4的左孩子2右上旋转作为4的根节点
(2)4节点右下旋转称为2的右孩子
(3)2的原右子树称为4的左子树
![]()
RR调整
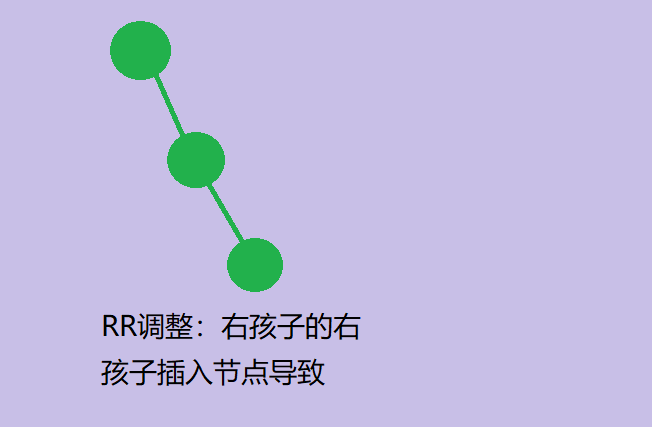
- RR:某分支节点的右孩子的右子树插入节点引起失衡
![]()
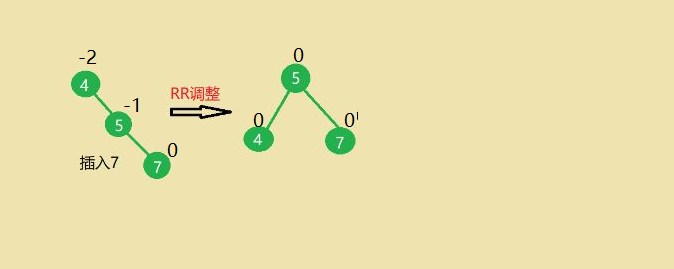
- 插入7导致节点4失衡,进行RR调整,左旋使之平衡。
(1)4的右孩子5左上旋转作为4的根节点
(2)4节点左下旋转称为5的左孩子
(3)5的原左子树称为4的右子树
![]()
LR调整
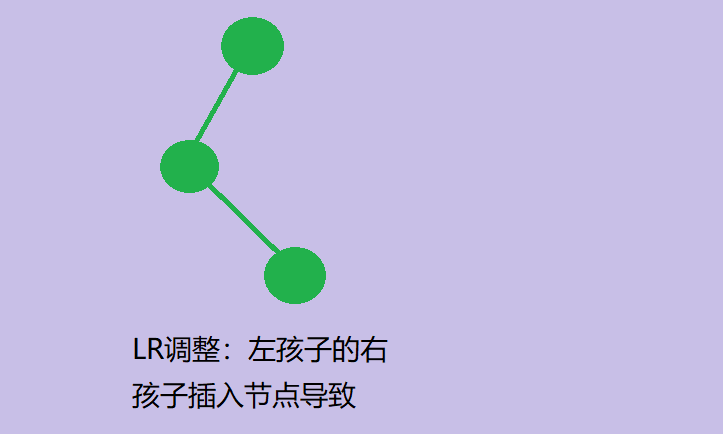
- LR:某分支节点的左孩子的右子树插入节点引起失衡
![]()
- 在15的左子树的右子树上插入结点,以插入的结点7为旋转轴, 先7进行左旋转,15再向右旋转。
(1)7向上旋转到15的位置,15作为7右孩子
(2)7原左孩子作为4的右孩子
(3)7原右孩子作为15的左孩子
![]()
RL调整
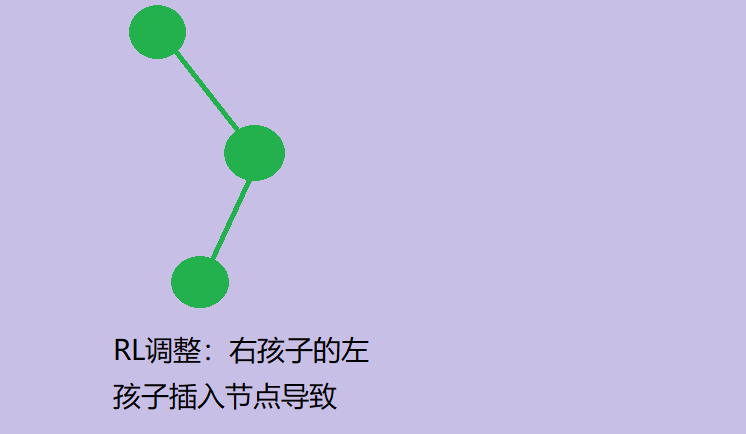
- RL:某分支节点的右孩子的左子树插入节点引起失衡
![]()
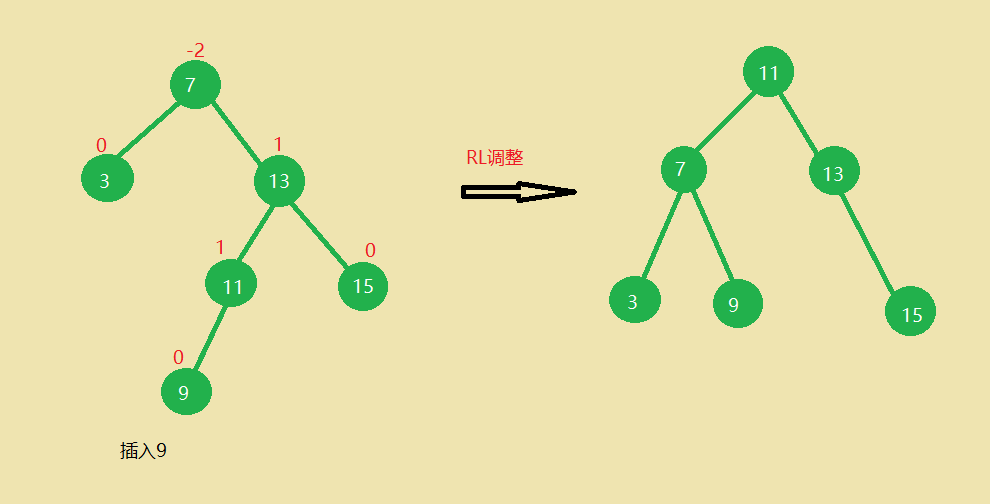
- 在7的右子树的左子树上插入结点,导致节点7失衡,进行RL调整,先进行右旋转,再左旋转。
(1)11向上旋转到7的位置,7作为11左孩子
(2)11原左孩子作为7的右孩子
(3)11原右孩子作为13的左孩子
B-树和B+树定义
B-树
- B树又称多路平衡查找树,B树中所有结点的孩子结点数的最大值称为B树的阶。
- 一棵m阶B树或空树,满足如下特性:
(1)树中每个结点至多有m棵子树,至多含有m-1个关键字
(2)若根结点不是终端结点,则至少有两棵子树
(3)除根结点外的所有非叶结点至少有m/2(取上界)棵子树
(4)所有叶子结点都在同一层次上
B-树的插入
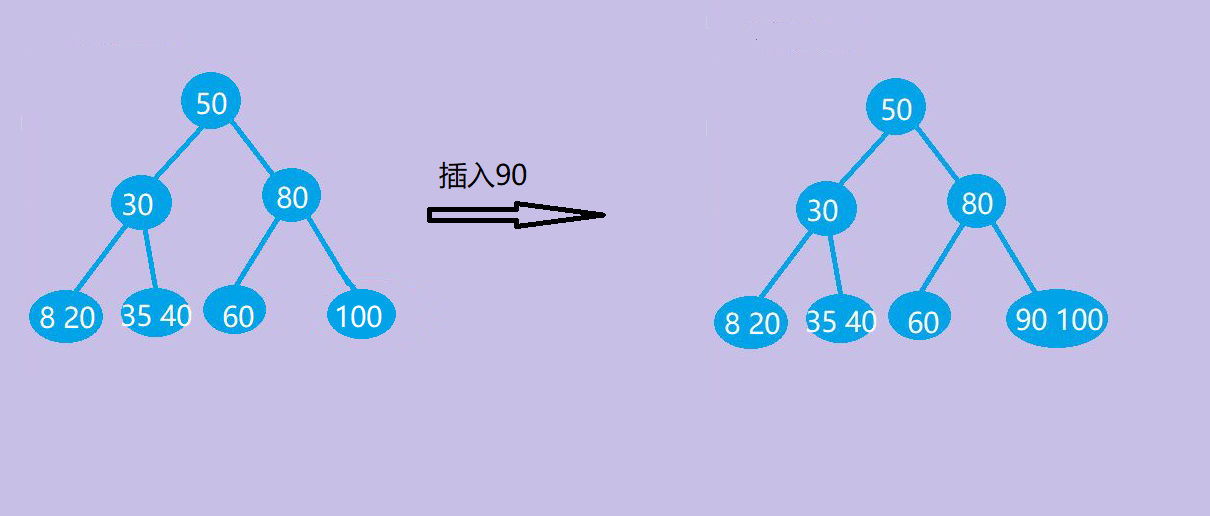
-
若插入后,不破会m阶B树的定义,即插入后结点关键字个数在属于区间[m/2(取上界)-1, m-1],则直接插入;
![]()
-
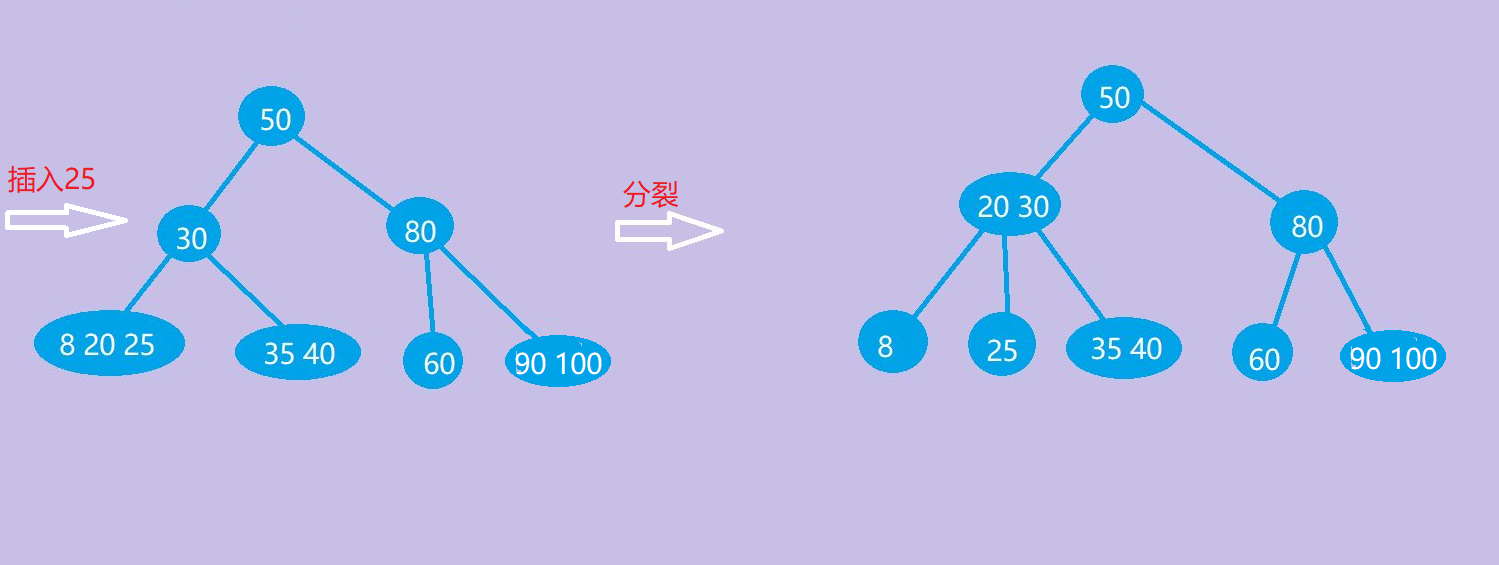
若插入后,关键字数量大于m-1,则对插入后的结点进行分裂:
插入后的结点中间位置m/2(取上界)关键字并入父结点中,中间结点左侧结点留在原先的结点中,右侧结点放入新的节点中,若并入父节点后,父结点关键字数量超出范围,继续想上分裂,直到符合要求为止。 -
插入25后,关键字数量大于2,则进行分裂:将节点20并入父结点30中,中间结点左侧结点8留在原先的结点中,右侧结点放入25,分裂完成。
![]()
B-树的删除
-
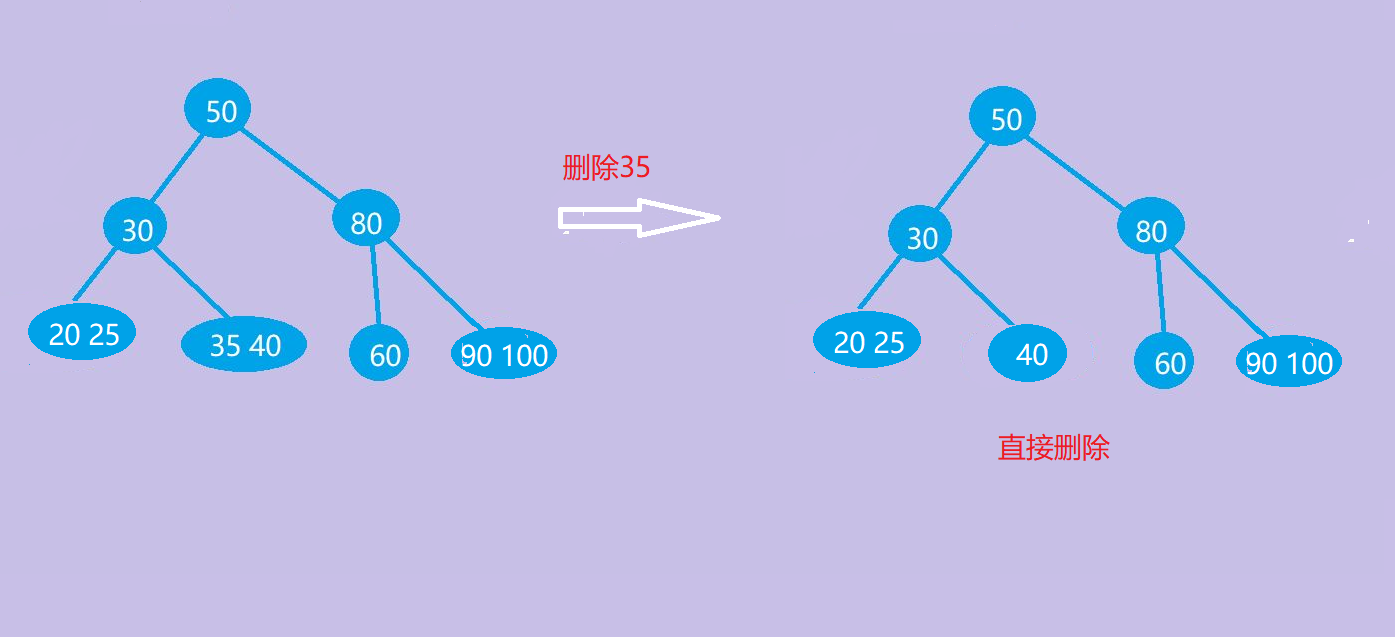
(1)直接删除
若被删除关键字所在结点关键字总数大于m/2(取上界)-1,则直接删除。
![]()
-
(2)兄弟够借
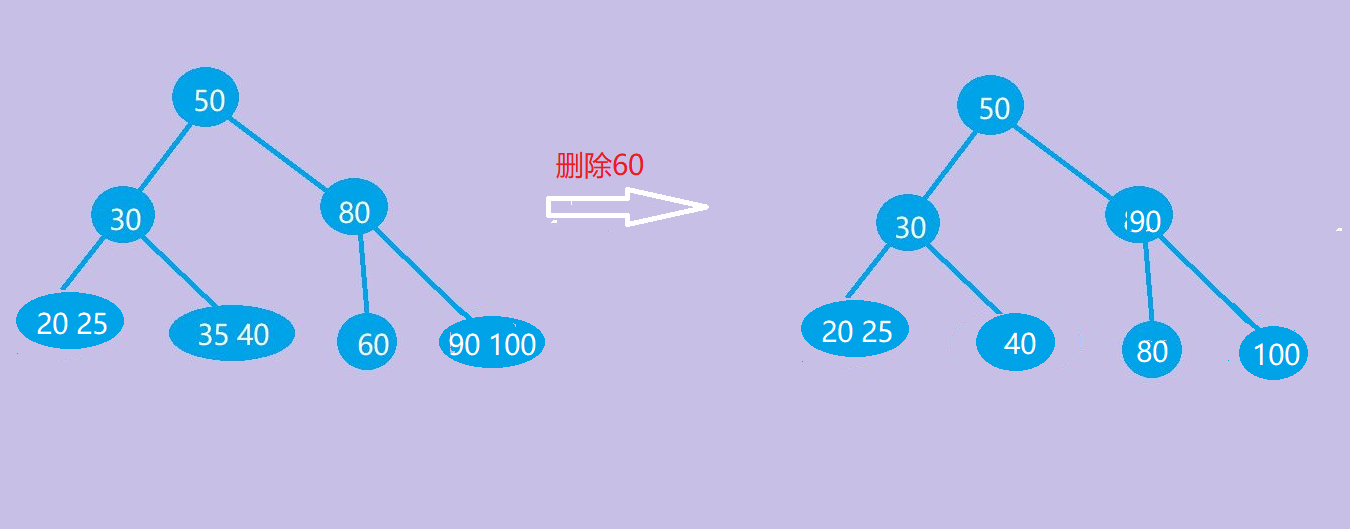
若被删除关键字所在结点关键字总数等于m/2(取上界)-1,且与此结点邻近的兄弟结点的关键字个数大于或等于m/2(取上界) ,则需要从兄弟结点借一个关键字,调整该结点、双亲结点和兄弟结点的关键字,使之满足B-树的定义 -
删除节点60,向右边兄弟节点借一个节点90,将90作为父亲节点,且原父亲节点80则作为其左孩子节点
![]()
-
(3)兄弟不够借
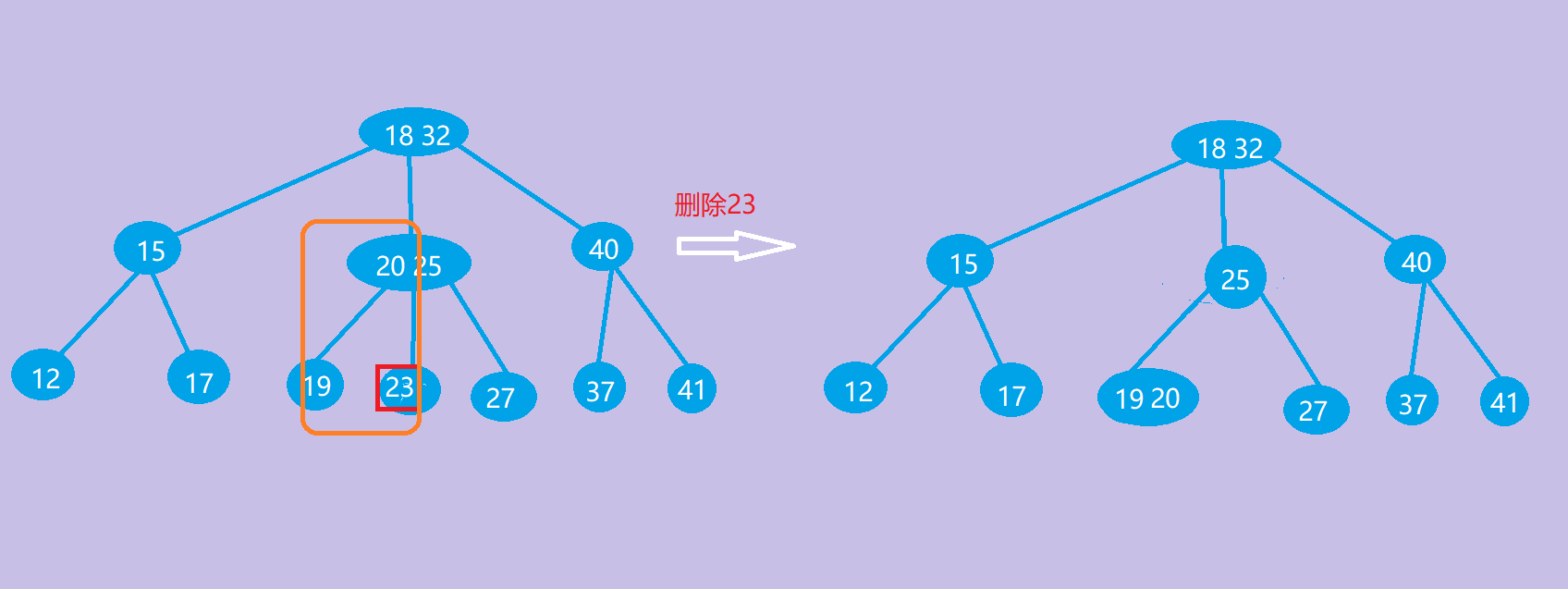
若被删除关键字所在结点关键字总数等于m/2(取上界)-1,且与此结点邻近的兄弟结点的关键字个数等于m/2(取上界)-1,则删除关键字,并与一个不够借的兄弟结点和双亲结点中两兄弟子树中间的关键字合并。合并后若双亲结点因减少一个结点导致不符合定义, 则继续执行以上步骤。
![]()
B+树
- 一棵m阶B+树满足如下特性:
(1)每个分支结点最多有m棵子树
(2)若根结点不是终端结点,则至少有两棵子树
(3)除根结点外的所有非叶结点至少有m/2(取上界)棵子树,子树和关键字个数相等
(4)所有分支结点中仅包含他的各个子结点中关键字的最大值及指向其子结点的指针
(5)所有叶结点包含全部关键字及指向相应记录的指针,叶结点中将关键字按大小顺序排列,并且相邻结点按大小顺序连接起来
散列查找
哈希冲突解决办法
线性探测法
- 线性探测法是从发生冲突的地址(设为do)开始,依次探测do的下一个地址(当到达下标为m-1的哈希表表尾时,下一个探测地址是表首地址0),直到找到一个空闲单元为止(当m≥n时一定能够找到一个空闲单元)
- 线性探测法的优点是解决冲突简单,一个重大的缺点是容易产生堆积问题。
- 例:将关键字序列{7,8,30,11,18,9,14}散列存储到散列表中,散列表的存储空间是一个下标从0开始的一维数组,散列函数为:H(key)=(key×3) mod 7,处理冲突采用线性探测再散列法,要求装填(载)因子为0.7。(2010全国考研题)
所构造出的散列表为:
![]()
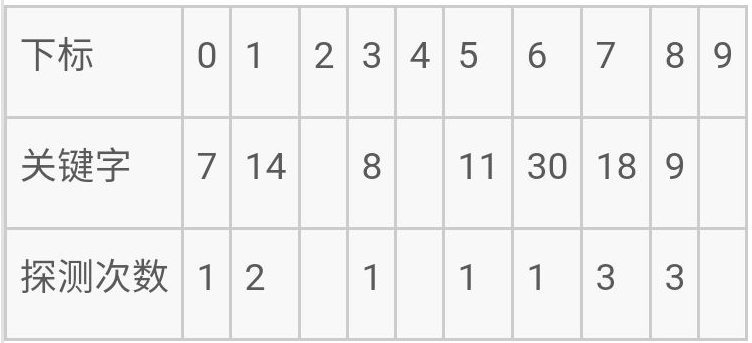
采用线性探测构造出的散列表为:
![]()
![]()
拉链法
- 拉链法是把所有的同义词用单链表链接起来的方法。它有以下优点:
(1)拉链法处理冲突简单,且无堆积现象,非同义词绝不会发生冲突,所以平均查找长度较短
(2)拉链法中各单链表上的结点空间是动态申请的,所以它更适合于造表前无法确定表长的情况
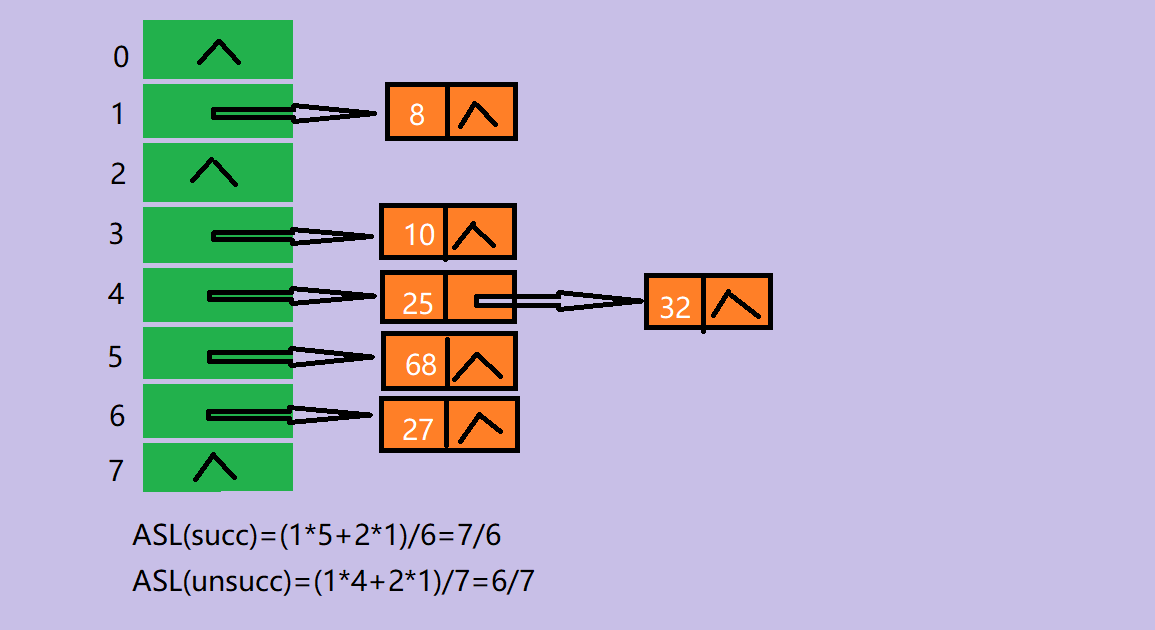
(4)在用拉链法构造的哈希表中,删除结点的操作更加易于实现 - 设一组初始记录关键字集合为(25,10,8,27,32,68),散列表的长度为8,散列函数H(k)=k mod 7,则用链地址法作为解决冲突的方法设计哈希表为:
![]()
哈希表结构体定义

哈希表插入及建表
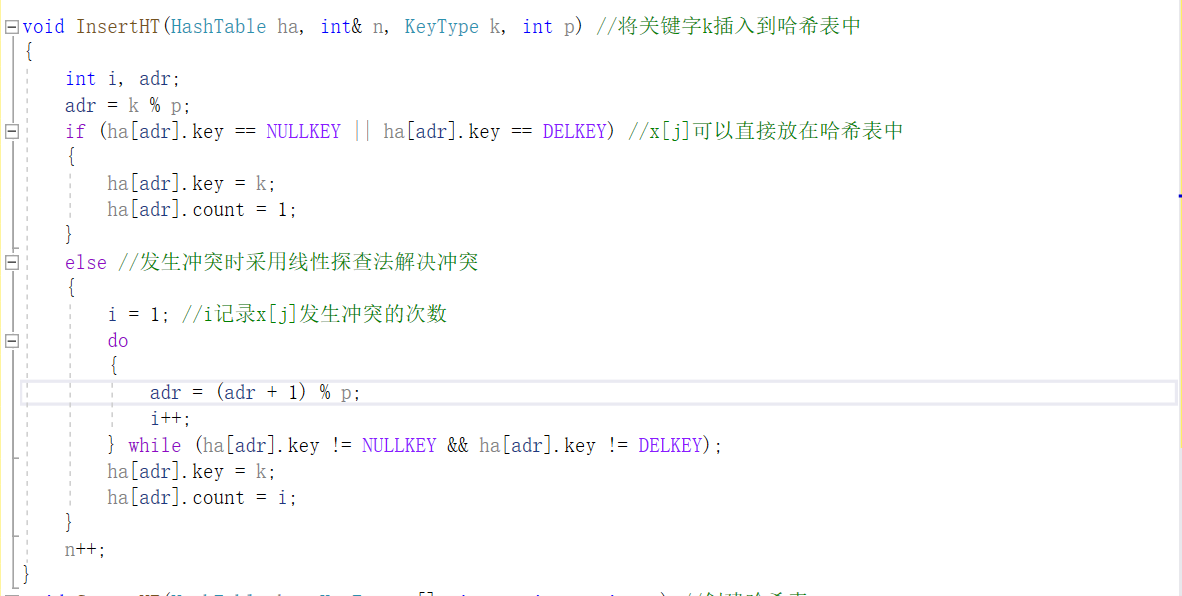

哈希表查找算法

哈希表删除算法

哈希链结构体定义
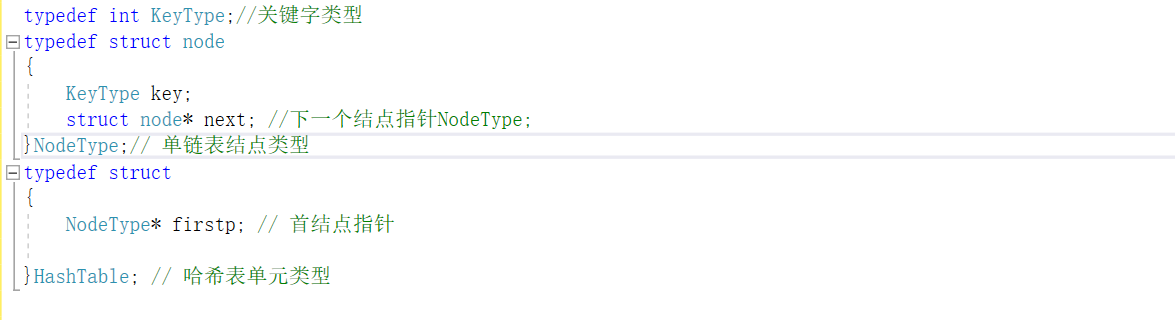
哈希链插入及创建


哈希链查找算法
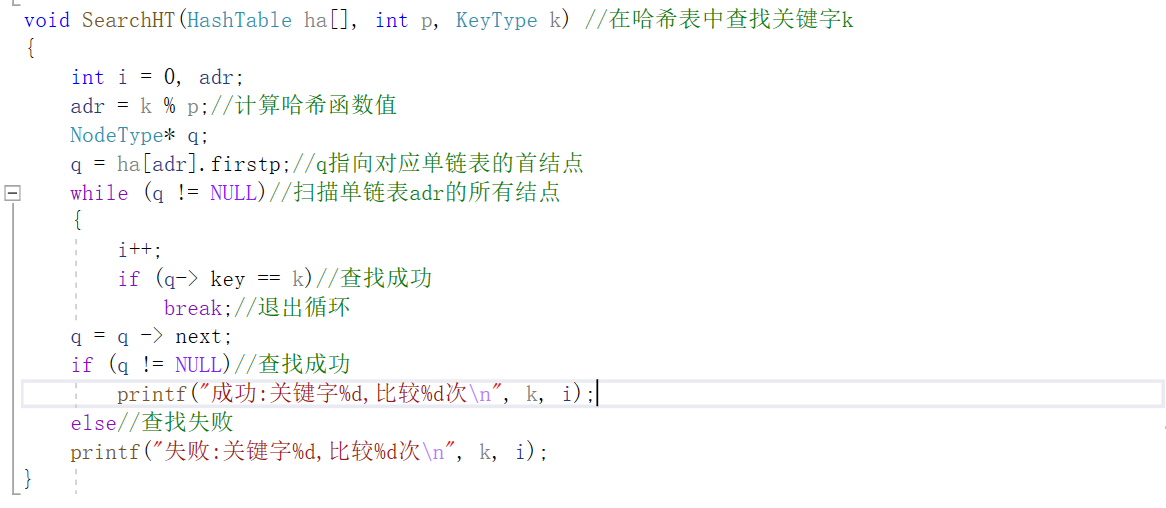
哈希链删除算法

1.2.谈谈你对查找的认识及学习体会。
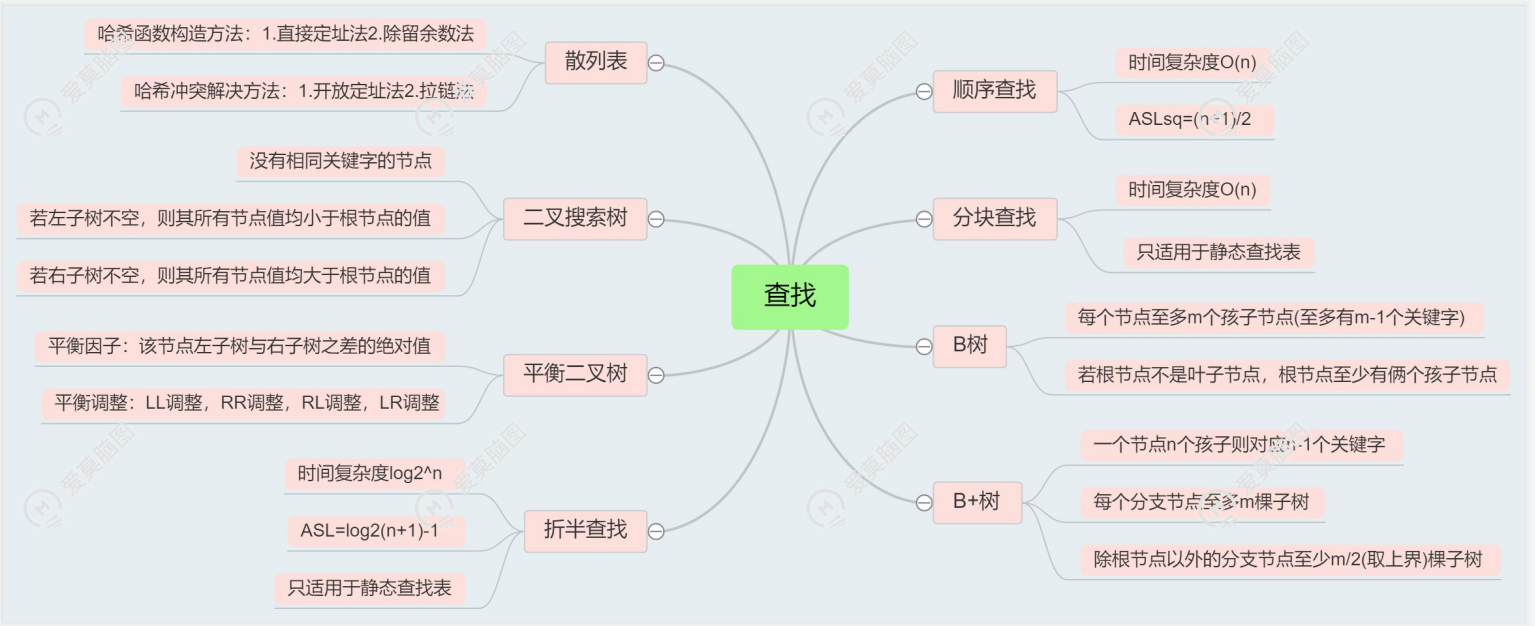
- 查找内容知识点比较多,线性表查找方法有顺序查找,折半查找,分块查找等,树表查找有B-树,平衡二叉树,哈希表,哈希链等,它们都各有优缺点,但是都能应用到相应问题中,使查找效率更高,存储空间更节约。在实际运用中,使用STL容器查找更为简便,代码更为精简。
2.PTA题目介绍
2.1 题目1:是否完全二叉搜索树
2.1.1 该题的设计思路
- 首先要建立二叉搜索树,再利用完全二叉树的性质判断其是否为完全二叉树,并层次遍历所有节点再输出其结果。
- 判断完全二叉树
![]()
![]()
- 若程序执行完所有节点都被访问过,则说明是完全二叉树,反之则不是完全二叉树。
2.1.2 该题的伪代码
bool IsCompleteTree(BSTree& T, int n)//判断是否为完全二叉树
{
初始化一个队列Q
if(根节点为空)
返回true
else
{
定义一个变量count计算访问了几个节点
将根节点入队
BSTree t;//初值为队首元素
while(t不为空)
{
将t的左孩子和右孩子入队
累计访问的节点
}
end while
}
if(所有节点都被访问过)
返回true
else
返回false
}
void LevelOrder(BSTree& T, int n)//层序遍历输出结点
{
初始化一个队列Q
定义一个数组data存储层序遍历的结果
将根节点入队
while(队列不为空)
{
取队首元素
给数组data赋值
if(左子树不空)
将左子树入队
if(右子树不空)
将右子树入队
}
输出层次遍历结果
}
void InsertBST(BSTree& T, int e)//向树中插入元素
{
if(初始树为空时)
给树中节点赋初值
else if(插入的数值比当前节点的值小)
{
将要插入的数值插入左子树
}
else if(插入的数值比当前节点的值大)
{
将要插入的数值插入右子树
}
}
void CreateBST(BSTree& T, int a[], int n)//创建二叉搜索树
{
树初始化为空
将输入的数值依次向树中插入
}
2.1.3 PTA提交列表
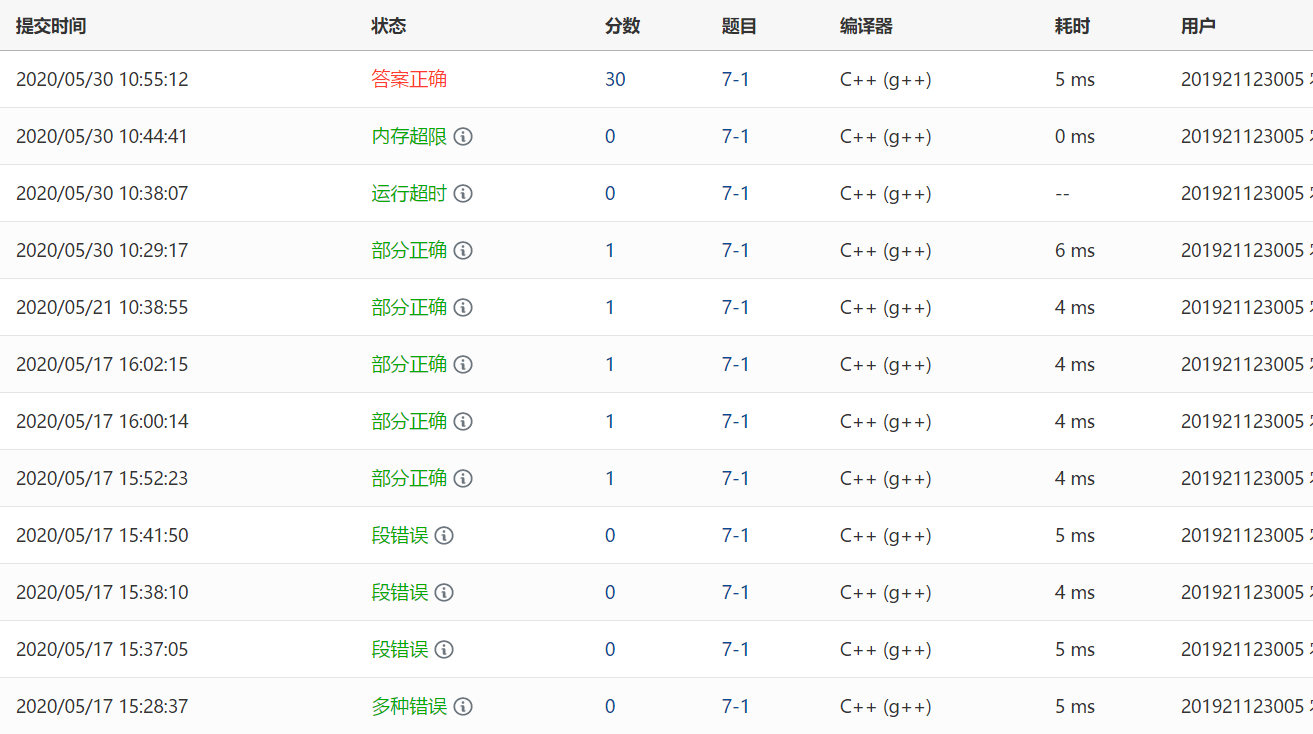
段错误:一开始写的时候创建二叉搜索树的函数有返回其根节点,但是在主函数里根节点是空的,后面函数调用就出错了。
部分正确:刚开始不清楚要满足什么条件才能判定是完全二叉树,怎么改都是答案错误,后来又换另一种方法,用一个变量记录访问过的节点,当程序执行完后,若所有节点都被访问过则说明是完全二叉树
2.1.4 本题设计的知识点
- (1)使用队列实现树的层次遍历
1.首先将根节点入队
2.遍历当前层所有节点,并用数组保存访问过的节点,然后将下一层的节点入队
3.最后得到的每一层节点的值依次输出 - (2)判断一棵树是否为完全二叉树
1.若当前访问节点左孩子为空,右孩子不为空,则该树不是完全二叉树
2.若当前访问节点左孩子不为空,右孩子为空;或者其左右孩子都为空,且该节点之后的队列中的节点都是叶子节点,则该树为完全二叉树
2.2 题目2:QQ帐户的申请与登陆
2.2.1 该题的设计思路
- 使用map容器存储账号与密码,可以处理QQ账号与密码一对一的数据处理,其账号与密码用数组方式插入。
2.2.2 该题的伪代码
void Check(int n, string str1, string str2)
{
数组str1存储账号,str2存储密码
for i=0 to n
{
输入一个字符ch
if(ch为N)
{
输入账号和密码
if(此账号已经注册过)
输出ERROR: Exist
else
将此账户密码保存入Q,输出New: OK
}
else if(ch为L)
{
输入账号和密码
if(此账号不存在)
输出ERROR: Not Exist
else
{
if(账号密码都匹配,登录成功)
输出Login: OK
else //帐户密码错误
输出ERROR: Wrong PW
}
}
}
end for
}
2.2.3 PTA提交列表

答案错误:map容器的使用搞不太清楚,账号是否注册过的条件Q.find(str1) == Q.end()不清楚。
2.2.4 本题设计的知识点
- 使用map得包含map类所在头文件#include"map"
- 所用到的map基本操作函数:find()--查找一个元素;end()--返回指向map末端的迭代器
- find()用于定位数据出现位置,当数据出现时返回数据所在位置的迭代器,若map中没有要查找的数据,则它返回的迭代器等于end()返回的迭代器。如本题中Q.find(str1) == Q.end()表示查找的账号不存在
2.3 题目3:航空公司VIP客户查询
2.3.1 该题的设计思路
- 创建一条哈希链存储顾客ID和飞行里程,用除留取余法查找地址,查找到相应ID时累计飞行路程。
2.3.2 该题的伪代码
HashTable* CreateHashTable(int n)//建哈希链
{
HashTable* p;
为p动态申请内存
确定哈希表最大长度
for(i=0 to p->Tablesize)
初始化哈希表
}
int Hash(HashTable* p, char key[])
{
for i=13 to 18
{
if(校验码为x)
index = index * 10 + 10;
else
index = index * 10 + key[i] - '0';
}
}
Node* Find(HashTable* p, char key[])
{
Node* q;
将下标index调整为合法位置
while(q不空)
继续往下查找会员信息
}
void Insert(HashTable* p, char key[], int L)
{
先检查key是否存在
if(key找不到)
{
头插法插入数据
复制下ID信息
记录路程长度
}
else
累计飞行路程
}
2.3.3 PTA提交列表
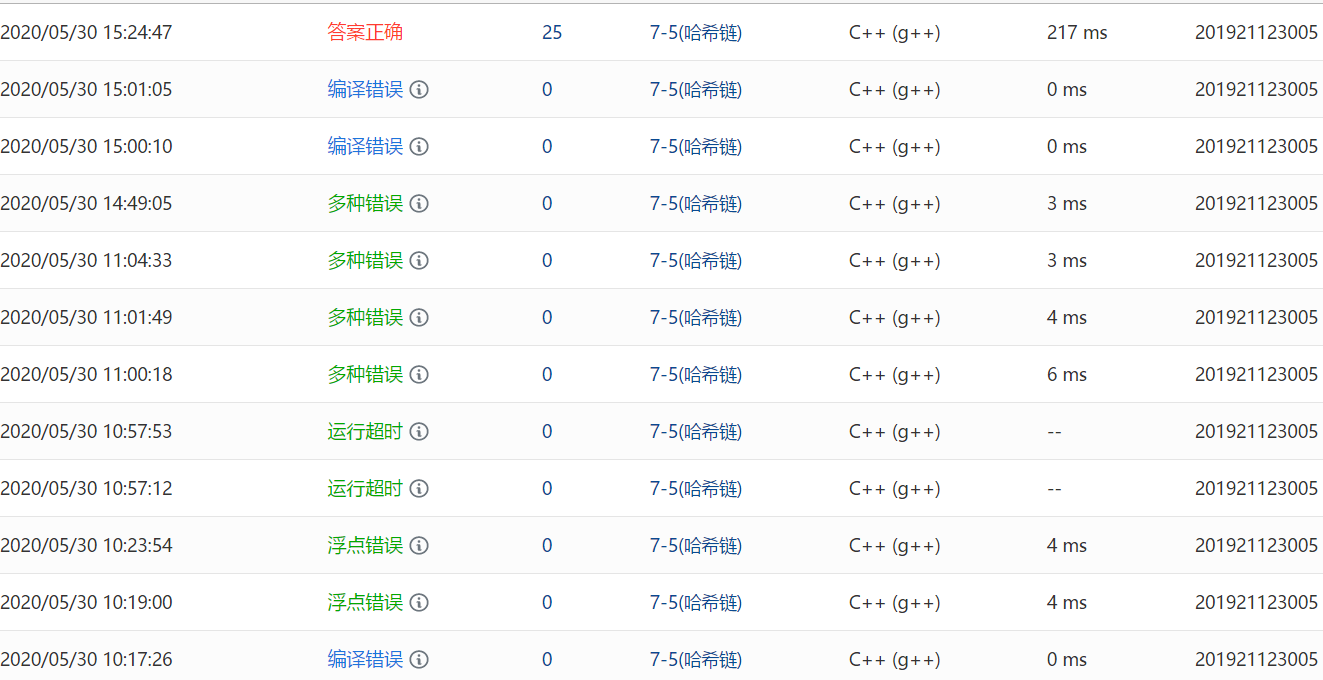
-
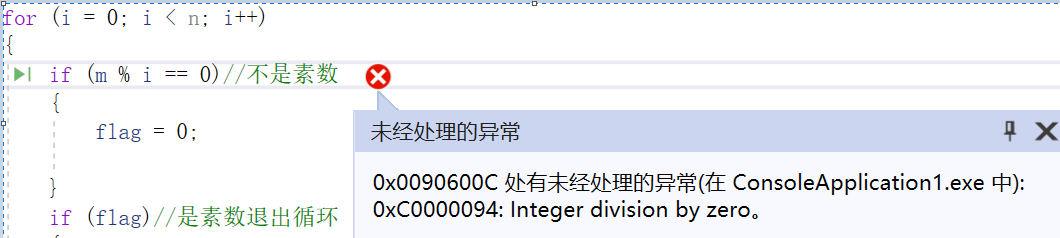
浮点错误:以前从未碰到这种错误,不懂是什么意思,在vs运行时提示:
![]()
-
浮点错误:然后我百度了一下浮点错误,才发现上面for循环中i从0开始,导致后面出现了一个数除以0的情况,所以i应该从2开始。
-
运行超时:可能是MAX的值取得太大了,本来是10000000,然后改成100000;然后就是把cout,cin换成scanf,printf,因为scanf,printf运行效率比cout,cin低。
2.3.4 本题设计的知识点
- 哈希链的创建,采用头插法。
- scanf,printf运行效率比cout,cin低。




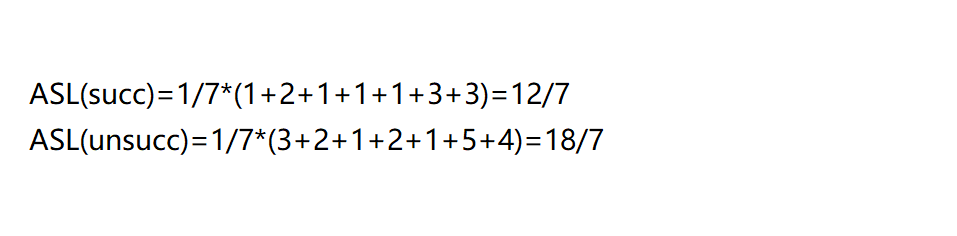



 浙公网安备 33010602011771号
浙公网安备 33010602011771号