GDUFE ACM-1059最大连续子序列(DP)

最大连续子序列

Time Limit: 1000ms

Problem Description:

   给定K个整数的序列{ N1, N2, ..., NK }，其任意连续子序列可表示为{ Ni, Ni+1, ..., 
Nj }，其中 1 <= i <= j <= K。最大连续子序列是所有连续子序列中元素和最大的一个， 
例如给定序列{ -2, 11, -4, 13, -5, -2 }，其最大连续子序列为{ 11, -4, 13 }，最大和 
为20。 
在今年的数据结构考卷中，要求编写程序得到最大和，现在增加一个要求，即还需要输出该 
子序列的第一个和最后一个元素。

Input:

测试输入包含若干测试用例，每个测试用例占2行，第1行给出正整数K( <= 1000000 )，第2行给出K个不超过100的整数，中间用空格分隔。当K为0时，输入结束，该用例不被处理。

Output:

对每个测试用例，在1行里输出最大和、最大连续子序列的第一个和最后一个元 
素，中间用空格分隔。如果最大连续子序列不唯一，则输出序号i和j最小的那个（如输入样例的第2、3组）。若所有K个元素都是负数，则定义其最大和为0，输出整个序列的首尾元素。 

Sample Input:

6
-2 11 -4 13 -5 -2
10
-10 1 2 3 4 -5 -23 3 7 -21
6
5 -8 3 2 5 0
1
10
3
-1 -5 -2
3
-1 0 -2
0

Sample Output:

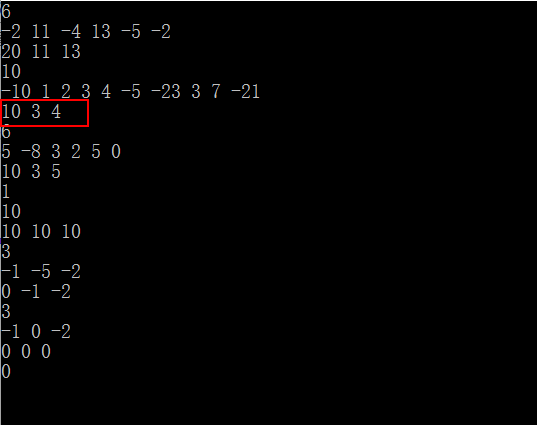
20 11 13
10 1 4
10 3 5
10 10 10
0 -1 -2
0 0 0

思路：if(f[i-1]>0)  f[i]=f[i-1]+a[i];
　　　　else f[i]=a[i];
如输入6
　　　-5 6 -1 5 4 -7

a[i]	-5	6	-1	5	4	-7
f[i]	-5	6	5	10	14	7

最后再对结果扫描一遍。
 
但题目加了”输出该子序列的第一个和最后一个元素。“，我被自己弄乱了，
WA的代码：

#include<bits/stdc++.h>
using namespace std;

int a[1000005],f[1000005];
int main()
{
    int k,max,num,first,last,b;
    while(~scanf("%d",&k),k!=0)
    {
        first=last=b=num=0;
        for(int i=0;i<k;i++)
        {
            scanf("%d",&a[i]);
            if(a[i]<0)
                num++;
        }
        max=f[0]=a[0];
        for(int i=1;i<k;i++)
        {
            if(f[i-1]+a[i]>=a[i])
                f[i]=f[i-1]+a[i];
            else{
                f[i]=a[i];
                b=i;
                }
        }
        for(int i=0;i<k;i++)
        {
            if(f[i]>max)
            {
                max=f[i];
                first=b;
                last=i;
            }
        }
        if(num==k)
            printf("0 %d %d\n",a[0],a[k-1]);
        else
            printf("%d %d %d\n",max,a[first],a[last]);
    }
    return 0;
}

经过修改之后才知道：

最后AC代码：

#include<bits/stdc++.h>
using namespace std;

int a[1000005],f[1000005];
int main()
{
    int k,max,num,first,last,b;
    while(~scanf("%d",&k),k!=0)
    {
        first=last=b=num=0;
        for(int i=0;i<k;i++)
        {
            scanf("%d",&a[i]);
            if(a[i]<0)
                num++;
        }
        max=f[0]=a[0];
        for(int i=1;i<k;i++)
        {
            if(f[i-1]+a[i]>=a[i])
                f[i]=f[i-1]+a[i];
            else
            {
                f[i]=a[i];
                b=i;
            }
            if(f[i]>max)
            {
                max=f[i];
                first=b;
                last=i;
            }
        }
        if(num==k)
            printf("0 %d %d\n",a[0],a[k-1]);
        else
            printf("%d %d %d\n",max,a[first],a[last]);
    }
    return 0;
}