1.学习总结(2分)
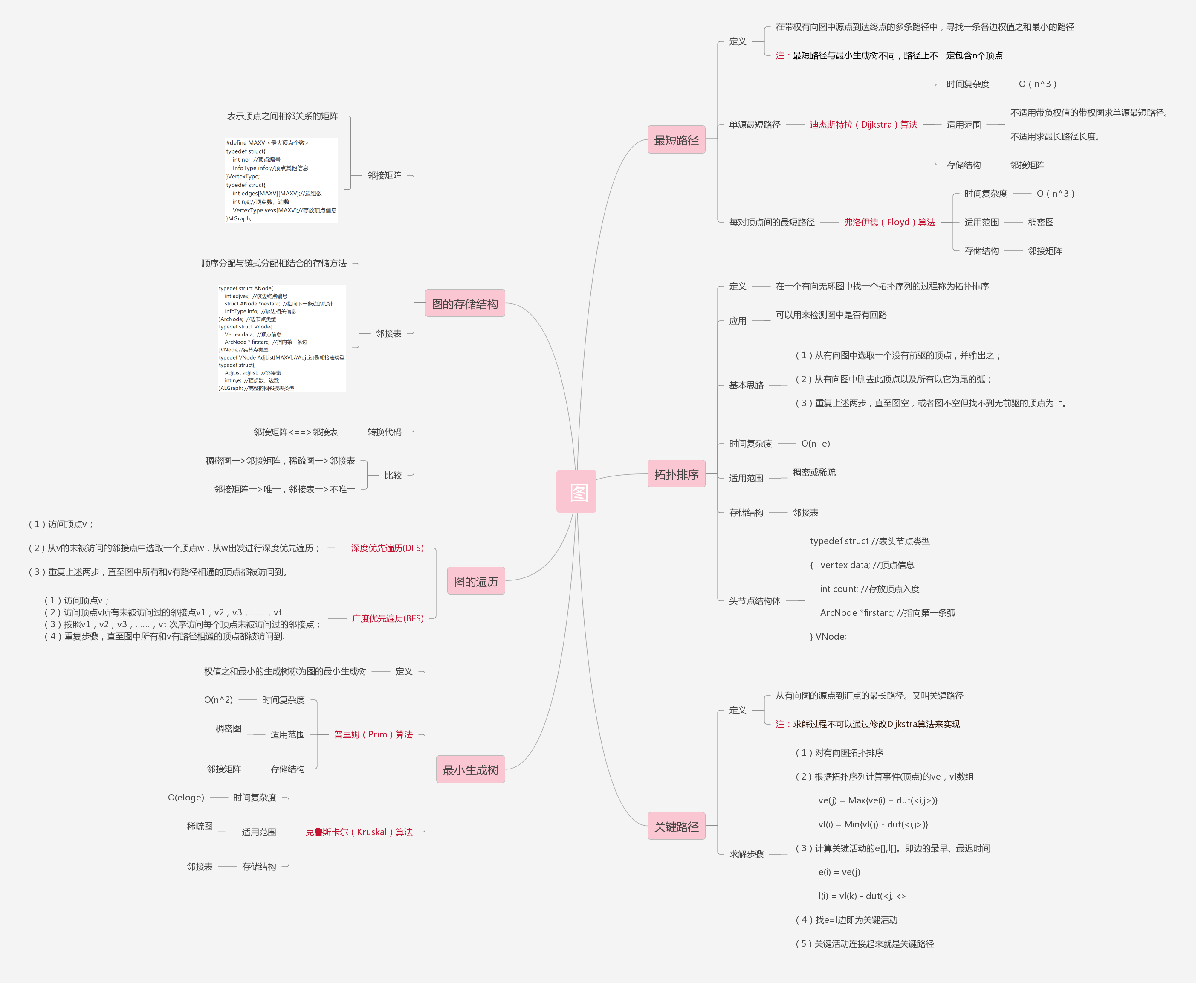
1.1图的思维导图
1.2 图结构学习体会
- 深度遍历算法:
(1)访问顶点v;
(2)从v的未被访问的邻接点中选取一个顶点w,从w出发进行深度优先遍历;
(3)重复上述两步,直至图中所有和v有路径相通的顶点都被访问到。
- 广度遍历算法
(1)访问顶点v;
(2)访问顶点v所有未被访问过的邻接点v1,v2,v3,……,vt
(3)按照v1,v2,v3,……,vt 次序访问每个顶点未被访问过的邻接点;
(4)重复步骤,直至图中所有和v有路径相通的顶点都被访问到.
- Prim算法:
(1)初始化U={v}。v到其他顶点的所有边为候选边;
(2)重复以下步骤n-1次,使得其他(n-1)个顶点被加入到U中:
①从候选边中挑选权值最小的边输出,设该边在V-U中的顶点是k,将k加入U中;
②考察当前V-U中的所有顶点j,修改候选边:若(j,k)的权值小于原来和顶点k关联的候选边,则用(k,j)取代后者作为候选边。
- Kruscal算法:
(1)置U的初值等于V(即包含有G中的全部顶点),TE的初值为空集(即图T中每一个顶点都构成一个连通分量)。
(2)将图G中的边按权值从小到大的顺序依次选取:
①若选取的边未使生成树T形成回路,则加入TE;
②否则舍弃,直到TE中包含(n-1)条边为止。
- Dijkstra算法:
(1)求出最短路径的顶点集合,用S表示
(2)第二组为其余未确定最短路径的顶点集合,用U表示
(3)源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路长度
- 拓扑排序算法:
(1)从有向图中选取一个没有前驱的顶点,并输出之;
(2)从有向图中删去此顶点以及所有以它为尾的弧;
(3)重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止
2.PTA实验作业(4分)
2.1 题目1:7-1 图着色问题
2.2 设计思路(伪代码或流程图)
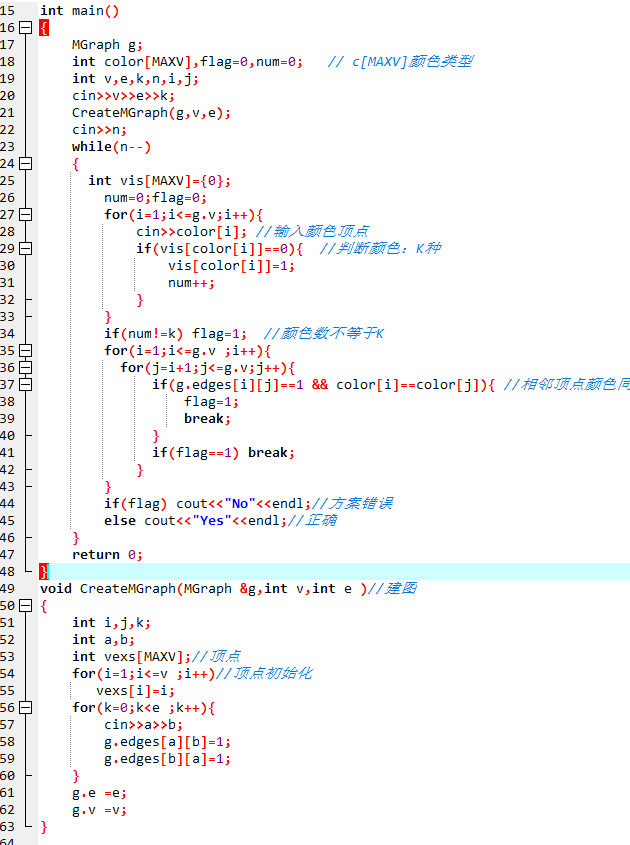
建立邻接矩阵
定义vis[MAXV]={0}标志颜色是否存在,0为不存在,1为存在
定义颜色种类num=0,flag表示方案正误,1为错误,0为正确;
for i=1 to g.v
输入颜色种类;
if 该颜色不存在{
颜色种类num++;
标记该颜色存在
}
end for
if 颜色种类不为k种,flag=1;
遍历每个顶点
if 两个顶点相邻并且颜色相同
flag=1;退出循环
if flag为1 输出NO
else 输出Yes
2.3 代码截图
2.4 PTA提交列表说明。
-
存在问题:

解决方法:在代码中添加颜色数不为k种情况的判断条件

-
答案错误:顶点遍历错误
解决方法:

2.1 题目2:7-2 排座位
2.2 设计思路(伪代码或流程图)
int main
{
初始化并查集f[i]
while(M--){
输入宾客及关系
if(是朋友)
调用find查找朋友
if (两宾客朋友相同)记录朋友关系;
else 记录敌人关系
}
while(K--){
输入两宾客
调用find函数查找其朋友,如果有共同朋友,则返回的值相同;
根据题意判断条件,并输出四种内容;
}
}
2.3 代码截图

2.4 PTA提交列表说明。
-
本题代码参照某度的写法,使用并查集
-
存在问题:

解决方法:

-
答案错误:运行出来的答案是正确的,所以这个错误一直找不出来,最后发现少了括号;

解决方法:

2.1 题目3:7-4 公路村村通
2.2 设计思路(伪代码或流程图)
建立邻接矩阵,将边权值初始化为INF
定义lowCost标记顶点是否被访问,min表示每条道路最低预算,cost表示最低成本
for i=1 to n
给lowcost置初值为map[1][i];
end for
遍历所有顶点
最小预算min置为INF;
if (顶点未被访问且图连通) {
最低预算min置为该边权值;
记录最近顶点的编号k;
}
if(图不连通) return -1;
累加最低成本
k顶点标记已访问
for j=1 to n
修改数组lowcost
end
2.3 代码截图

2.4 PTA提交列表说明。
-
答案错误:

解决方法:在代码中添加m<n-1时的判断条件

-
答案错误:
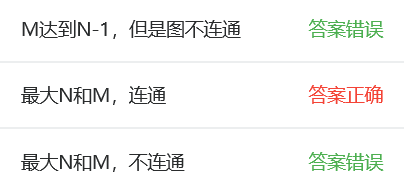
解决方法:不连通的情况没有考虑准确。加一个判断不连通的语句。

3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:1.5
4. 阅读代码(必做,1分)
- 这是黄毓颖同学的排座位的代码,使用的是图的知识,利用广度遍历寻找每个人与其他人的关系并记录。
#include<bits/stdc++.h>
using namespace std;
int pre[105];
int visited[105];
typedef struct
{
int edges[105][105];
int n,e;
}MGraph;
void CreateMGraph(MGraph &g,int n,int e);
void BFS(MGraph g,int v);
int main()
{
MGraph g;
int n,m,k,i,j,a,b,flag;
cin>>n>>m>>k;
for(i=0;i<105;i++)
pre[i]=i;
CreateMGraph(g,n,m);
BFS(g,1);
for(i=1;i<=k;i++)
{
flag=0;
cin>>a>>b;
if(g.edges[a-1][b-1]==1)//直接朋友关系
{
cout<<"No problem"<<endl;
}
else if(g.edges[a-1][b-1]==0)
{
if(pre[a-1]==pre[b-1])//间接朋友关系
cout<<"No problem"<<endl;
else
cout<<"OK"<<endl;//不是朋友 也不是敌人
}
else
{
for(j=0;j<n;j++)
{
if(g.edges[a-1][j]==1&&g.edges[b-1][j]==1)
{
flag=1;
break;
}
}
if(flag==1||pre[a-1]==pre[b-1])//是敌人,但有共同好友
cout<<"OK but..."<<endl;
else
cout<<"No way"<<endl;//单纯的敌对关系
}
}
return 0;
}
void CreateMGraph(MGraph &g,int n,int e){
int i,j,a,b,relation;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
g.edges[i][j]=0;
for(i=0;i<e;i++)
{
cin>>a>>b>>relation;
g.edges[a-1][b-1]=relation;
g.edges[b-1][a-1]=relation;
}
g.n=n;
g.e=e;
}
void BFS(MGraph g,int v) //广度遍历
{
int i;
queue <int> q;
visited[v]=1;
q.push(v);
while(!q.empty())
{
v=q.front();
q.pop();
for(i=0;i<g.n;i++)
{
if(g.edges[v-1][i]==1&&visited[i+1]==0)
{
visited[i+1]=1;
pre[i]=pre[v-1];
q.push(i+1);
}
}
}
}





