|
原题见 莫贝特 的博客,意思是在1-1000的有序数列中,再随机插入一个数,这个数大小还是在1-1000之间,而且插入位置要保证插入后数列仍然有序。 |
在 莫贝特 的博客中,他的算法是将(1001个数字的和)- (1000个数字的和)= 重复数字,这种算法思路简单,但是时间复杂度是最高的,共进行了2000次循环,至于留言中的其他算法也基本上属于线性查找,线性查找的时间复杂度是O(N),对于这道题目,运气最好的时候第一次就能找到,运气最差的时候,要找1000次,平均要找500次。
然而,如果我们考虑到这是一个有序数列,而且只有两个重复数,二分折半查找法就一跃而出了,对数据结构和算法有了解的人都知道,二分查找法是有序数列最好的查找算法。
具体思路是:
1)left=0
2)right=10001
3)如果 left 和 right 中间那个位置 pos 的数值等于位置编号 pos,则:
4)left=pos,否则:
5)right=pos
6)如果(right-left>1),则重复步骤 3)-6),直到 right-left=1, pos 就是要查找的数
这几天正在看 Python ,就用 Python 实现了一个,1000个数只需查找10次,一万个数13次,十万个数17次,一百万个数20次,时间复杂度 O(logN),速度很快。下面上代码:
#!/usr/bin/python
# -*- coding: GBK -*-
import random
# 生成数列,一万个数
arr_length=100001
list=range(1,arr_length)
#插入一个随机数
rnd=random.randrange(1,arr_length)
list.insert(rnd-1,rnd)
print '\n重复数为:'+ str(rnd)
print'\n开始查找'
# 正式开始查找算法
left=0
right=arr_length
count=0
while ((right-left)>1):
pos=(left+right)/2
count=count+1
print '第 %d 次定位:%d' % (count,pos)
if (list[pos]==pos):
right=pos
else:
left=pos
print '\n查找结果:',list[left]
# -*- coding: GBK -*-
import random
# 生成数列,一万个数
arr_length=100001
list=range(1,arr_length)
#插入一个随机数
rnd=random.randrange(1,arr_length)
list.insert(rnd-1,rnd)
print '\n重复数为:'+ str(rnd)
print'\n开始查找'
# 正式开始查找算法
left=0
right=arr_length
count=0
while ((right-left)>1):
pos=(left+right)/2
count=count+1
print '第 %d 次定位:%d' % (count,pos)
if (list[pos]==pos):
right=pos
else:
left=pos
print '\n查找结果:',list[left]
输出结果如下图: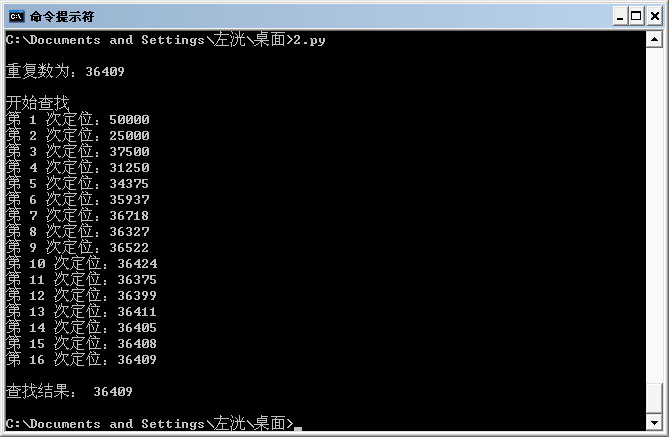 //==========================================
//==========================================



 浙公网安备 33010602011771号
浙公网安备 33010602011771号