一:学习总结
1查找结构思维导图
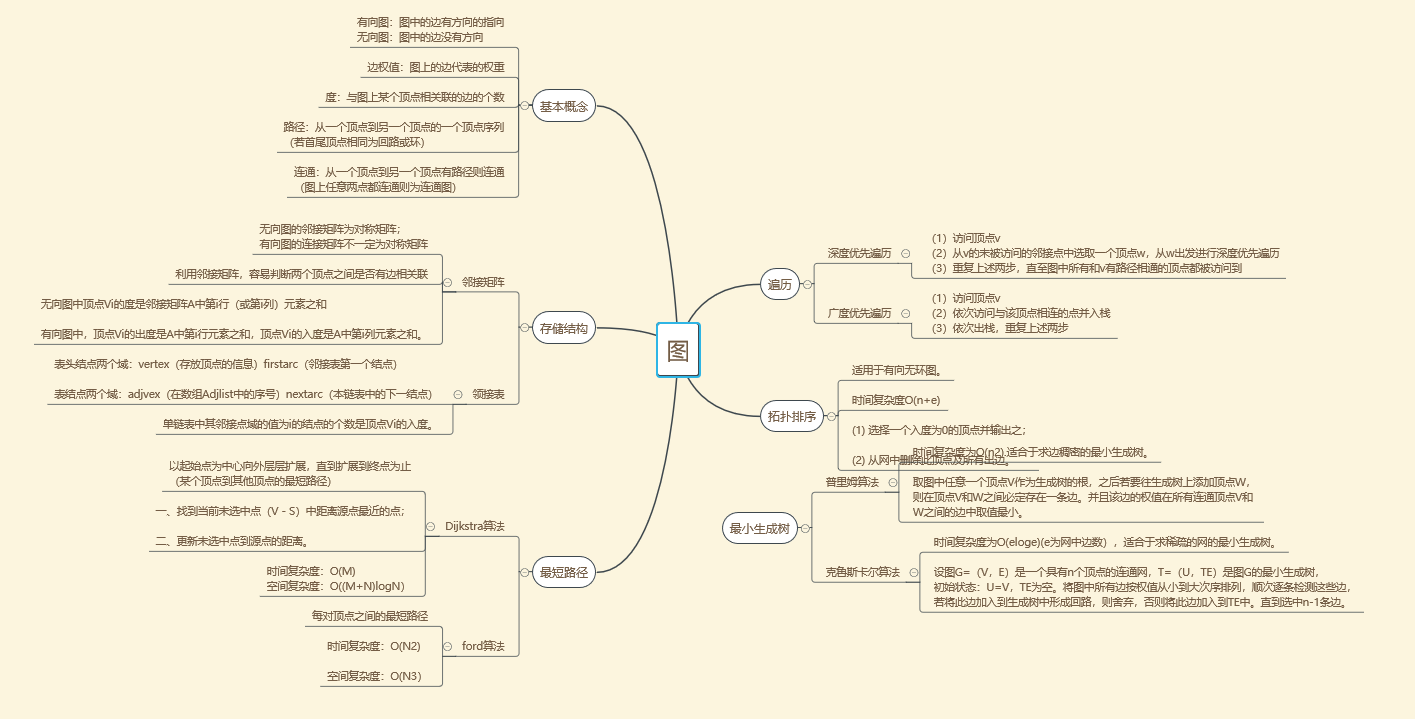
2查找学习体会
遍历:
- 深度遍历算法(DFS):dfs先访问起始点v0,然后以它的领接点为起始点递归访问领接点.每有一条路走到尽头,就回到上一个路口,选择另一条路再走到底,直到所有结点都已访问过.沿途标记结点已被访问。
- 广度遍历算法(BFS): bfs从第一个顶点开始访问其领接点,将这些点入栈(队).然后循环取出栈顶(队首)作上述操作,直到所有点都访问过.访问过程中标记顶点,不重复访问。
最短路径:
- Dijkstra算法:求原点到其他点的距离;这种算法只能解决权值非负的图(可以求出单源点到其他顶点的最短距离,算法的复杂程度比floyd算法稍微低一些)。
- Floyd算法:时间复杂度比较高,不适合计算大量数据;特点:可以求多源最短路,权值同样不能为负。
最小生成树(Prim和Kruscal算法):
- Prim 算法从任意一个顶点开始,每次选择一个与当前顶点集最近的一个顶点,并将两顶点之间的边加入到树中。
- Kruscal 算法先将每个顶点放入其自身的数据集合中。然后,按照权值的升序来选择边。当选择每条边时,判断定义边的顶点是否在不同的数据集中。如果是,将此边插入最小生成树的集合中,同时,将集合中包含每个顶点的联合体取出,如果不是,就移动到下一条边。重复这个过程直到所有的边都探查过。
- 当题中边的数目较为复杂时,选用prim算法;一般选kruscal算法,理解起来比较简单。
拓扑排序:
- 将图按前后顺序组织排列起来,前后顺序是指在排序结果中,前面的顶点可能是有一条简单路径通向后面的顶点的,而后面的顶点是肯定没有一条简单路径通向前面的顶点的。
二:PTA实验作业
题目1:排位置
1设计思路
//这道题建图和主函数没什么特别的,主要就判断关系的函数
void judge()
输入两个宾客的编号
如果两个人是朋友,直接输出"No problem";
如果两个人没有关系,直接输出 "OK";
剩下的就是两个是敌人:
遍历顶点,如果两个人存在公共好友,即输出 "OK but...";
否则就输出"No way";
2代码截图

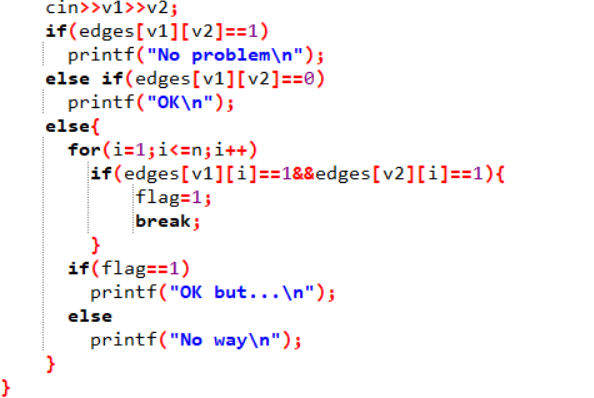
3PTA提交列表说明
答案错误:一开始并不知道要如何快速确定如果是敌人的话,他们是否有有公共好友;

然后想到可以遍历顶点来判断他们是否有公共朋友,所以过了另一个测试点;

但是出现运行超时,但是改小以后又出现了最大答案错误,就改用了全局变量。
题目2: 修建道路
1设计思路
定义整型变量count记录兴建的路的长度,n为村庄的数目,flag表示村庄之间的距离;
Q为兴建完的路数目,v1,v2表示村庄的编号;
for i=1 to i=n
for j=1 to j=n do
输入两个村庄之间的距离,用二维数组构建图;
for i=1 to i=Q do
输入v1,v2;
v1,v2两个村庄之间的距离改为1; //这样用prim算法计算最短路径时,一定会选择该条已建完的路径
count=prim(n)-Q; //Q的值就相当于已经建完的路的长度和,减去后即可得到新建公路的长度的最小值
2代码截图

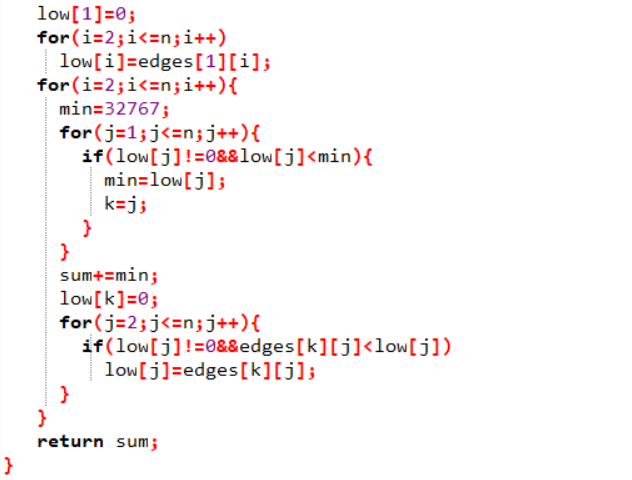
3PTA提交列表说明

部分正确1:一开始的思路是算出最短路径,然后减去已建的即可,但是测试点只有一个正确。
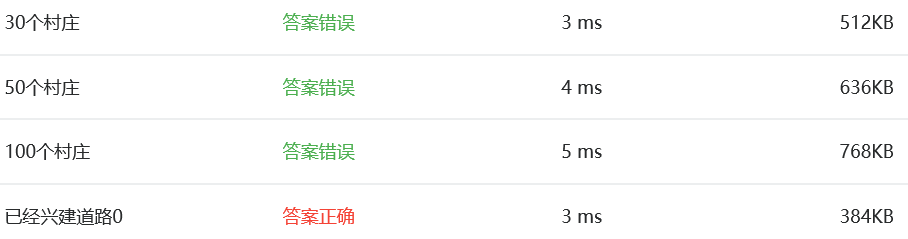
从示例的输出结果来看,由于已建的路不一定是最短的,故这样算出来的答案一定是错的!!!也许已建的路根本不在最短路径之内,所以必须要修改已建的路。我的思路是:怎样修改才能让已建的路被选入最短路径中并知道它的长度,这样既可以算最短路径又囊括了已建的路,最后减去已经建完的路的长度和,即可得到新建公路的长度的最小值。我选择了把已建完的两个村庄之间的距离改为1。
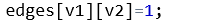
部分正确2:按如上修改后,提交结果中,示例的那个测试点通过了,但其他的测试点仍然不行,我就有点不知所措了,因为照示例来讲确实就是这个思路,没道理过不了。后来想到,在算最短路径时,不一定会算v1到v2的路,也可能算的是v2到v1的路,同一条路为什么我之前没有一起改呢! 抱着尝试的心态试了一下,果然就是这个地方出现了问题。
抱着尝试的心态试了一下,果然就是这个地方出现了问题。
题目3: 旅游规划
1设计思路
定义整型数组dist[]记录出发地的城市到其他城市的最短距离;
path[]记录路径,cost[]记录花费,N[]用来判断已确定路径;
for i=1 to i=n-1 do
for j=0 to j<n do
找到离图最近的顶点 v;
将 v 加入图中;
for j=0 to j<n do
若与v1连接且还没加入图的点
若 新的路线比原路线短 || 新路线和原路线等长但新路线比较便宜
更新数据
2代码截图


3PTA提交列表说明


部分正确:一开始只通过了最小的情况,从提示中可知还存在距离相同但更便宜的路径,所以加了一个判断;后面还是有一个测试点无法通过,重新再对照题目,看到城市编号从0~N-1,发现我在初始化的时候,从1开始,改了以后正确了。
三:截图本周题目集的PTA最后排名
1 PTA排名:

2 我的得分:231
四:阅读代码
有个城市叫做H市。其中有很多个村庄,村庄之间通信基本靠吼,交通基本靠走,很不方便。这个市长知道了这个情况,为了替市民着想,决定修建高铁。每修建一米花费1美元。现在市长请了最著名的工程师来修建高铁,自然这个工程师会让修建高铁的费用最少。不幸的是,在修建了高铁之后就病逝了。现在市长希望知道在修建完成的这些高铁路中最长的一段高铁路花费了多少美元,
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX_V = 510;
const int INF = 0x3f3f3f3f;
int cost[MAX_V][MAX_V]; //cost[u][v]表示边e=(u,v)的权值(不存在的情况下设为INF)
int mincost[MAX_V]; //从集合X出发的每个变得最小权值
bool used[MAX_V]; //顶点i是包含在集合X中
int V; //顶点数
int prim(){
for(int i = 0;i < V;i ++){ //初始化
mincost[i] = INF;
used[i] = false;
}
mincost[0] = 0;
int res = 0;
while(true){
int v = -1;
for(int u = 0;u < V;u ++){ //从不属于X的顶点中选取从X到其权值最小的顶点
if(!used[u] && (v == -1 || mincost[u] < mincost[v]))
v = u;
}
if(v == -1) break;
used[v] = true; //把顶点v加入到X
res = max(res, mincost[v]);//取已经生成最小生成树中最大的
for(int u = 0;u < V;u ++){
mincost[u] = min(mincost[u], cost[v][u]);
}
}
return res;
}
int main(){
int T,i,j;
scanf("%d",&T);
while(T --){
scanf("%d", &V);
for(i = 0;i < V;i ++){
for(j = 0;j < V;j ++){
scanf("%d",&cost[i][j]);
}
}
printf("%d\n", prim());
}
return 0;
}





