一:学习总结
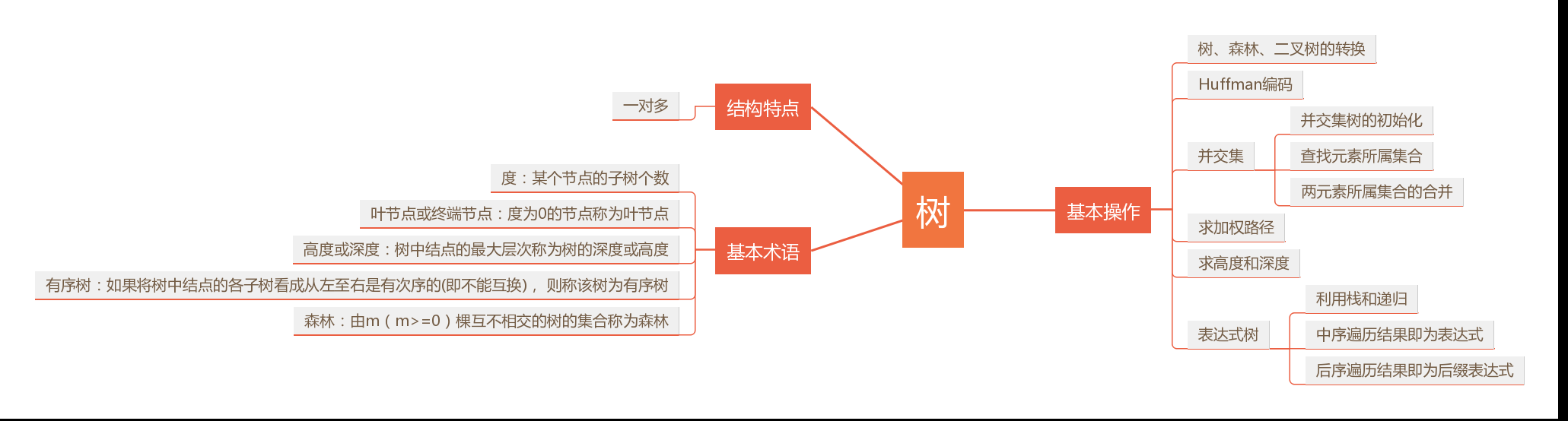
1树结构思维导图

补充:
2 树结构学习体会
很多细节的知识点要弄懂并记住真的挺困难的,像层次遍历建树的代码,先中后序遍历的代码,已知先序和中序求后序,已知中序和后序求先序的代码,还有线索化,哈夫曼树编码等等;从一对一的关系到一对多的关系,数与数之间的关系变得复杂,而且树的操作与应用很广泛,同时比较难掌握,所以需要花更多的时间来学习。
二:PTA实验作业
题目1:表达式树
1设计思路
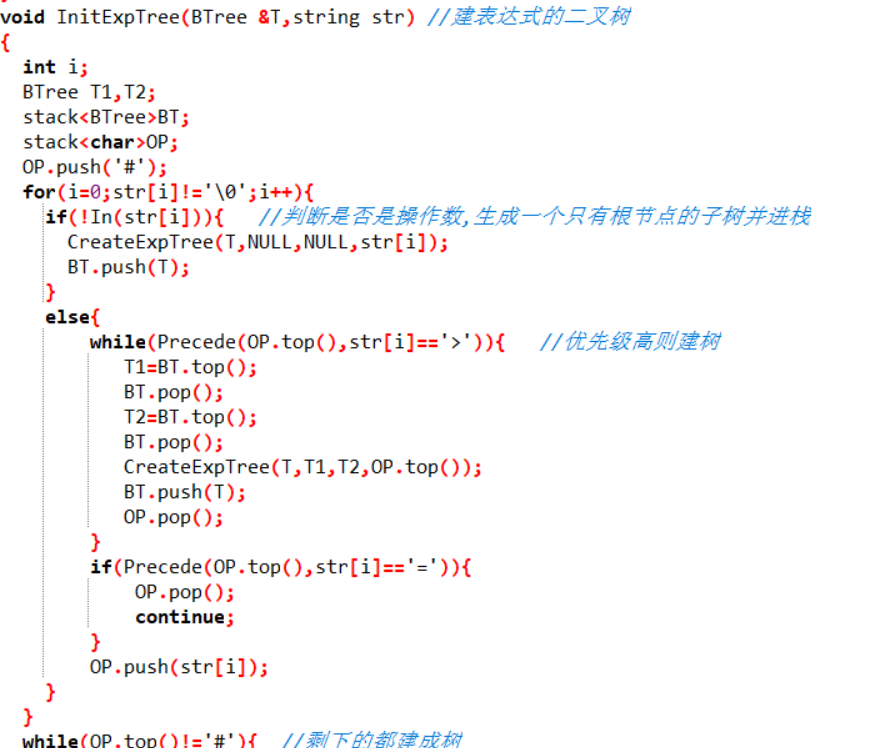
InitExpTree(BTree &T,string str) //建表达式的二叉树
建树栈BT;
建运算符栈OP,栈底为“#”;
for i=0 to str[i]!='\0' do
判断是否是操作数:
若是生成一个只有根节点的子树并进栈;
否则:
while 运算符的优先级高于栈顶 do
树栈中取两个结点作为树T的左右孩子;
T进BT;
if 运算符的优先级等于栈顶 OP栈顶出栈;
if 运算符的优先级低于栈顶 运算符进OP;
while OP.top()不是 '#' do
树栈中取两个结点作为树T的左右孩子;
T进BT;
EvaluateExTree(BTree T)//计算表达式树,利用递归
if In(T->data)为字符 do
字符为'+': 左子树表达式的值 + 右子树表达式的值
字符为 '-': 左子树表达式的值 - 右子树表达式的值
字符为 '*': 左子树表达式的值 * 右子树表达式的值
字符为 '/': 判断除数是否为零:左子树表达式的值 / 右子树表达式的值
else
返回 T->data-'0';
2代码截图

题目2:还原二叉树
1设计思路
输入树中结点总数,再输入先序和中序遍历序列;
根据先序和中序遍历序列建树;
用函数求该树的高度;
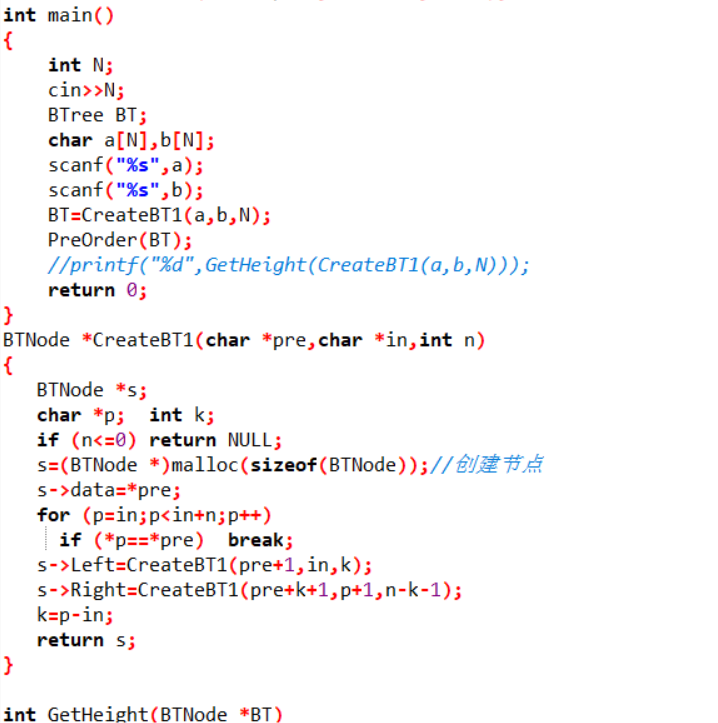
//根据先序和中序遍历序列建树
BTNode *CreateBT1(char *pre,char *in,int n)
{
if 树中结点总数 do
return NULL;
创建节点并指向根节点;
在中序遍历序列中找到根节点位置并记为K;
创建左子树:CreateBT1(pre+1,in,k);
创建左子树:CreateBT1(pre+k+1,in+k+1,n-k-1);
}
//求该树的高度;
int GetHeight(BTNode *BT)
{
if 根节点 do
return 0;
else{
HL=GetHeight(BT->Left);
HR=GetHeight(BT->Right);
返回深度较大的H
}
}
2代码截图

3PTA提交列表说明

没有找好根节点在中序中的位置,然后导致左子树右子树结点个数错误,树构建失败。
题目3:二叉树叶子结点带权路径长度和
1设计思路
定义全局变量count为叶子结点带权路径长度和
输入字符串:
if 空 do
输出零 //树空
else
建树,求叶子结点带权路径长度和
输出count;
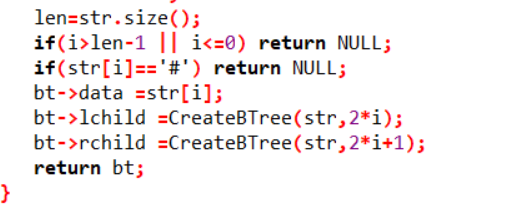
//用层次法建树
//用递归求叶子结点带权路径长度和
void GetHeight(BTree BT,int H)
{
if BT为叶子结点 do
累加结点带权路径长度
else
GetHeight(BT->lchild,H+1);
GetHeight(BT->rchild,H+1);
}
2代码截图

3PTA提交列表说明

部分正确:为零的情况正确,其余错误
示例结果: 
错误点:str为字符串类型,则计算结点带权路径长度时应减去‘0’。
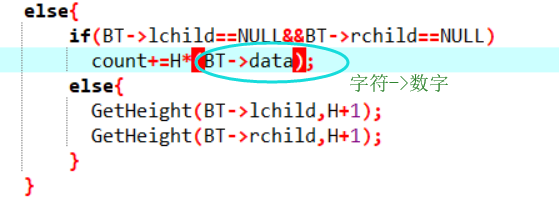
三:截图本周题目集的PTA最后排名
1 PTA排名:

2 我的得分:155
四:阅读代码
有一棵树,输出某一深度的所有节点,有则输出这些节点,无则输出EMPTY。该树是完全二叉树。
输入:
输入有多组数据。
每组输入一个n(1<=n<=1000),然后将树中的这n个节点依次输入,再输入一个d代表深度。
输出:
输出该树中第d层得所有节点,节点间用空格隔开,最后一个节点后没有空格。
#include<stdio.h>
#include<math.h>
int main() {
int n, d;
int tree[1002];
while (scanf("%d", &n) != EOF) {
for (int i = 1; i <= n; i++) {
scanf("%d", &tree[i]);
}
scanf("%d", &d);
int left = (int) pow(2, d - 1);
int right = (int) pow(2, d) - 1;
if (left > tree[n]) {
printf("EMPTY\n");
}
bool isFirst = true;
for (int i = left; i <= n && i <= right; i++) {
if (isFirst) {
printf("%d", tree[i]);
isFirst = false;
} else {
printf(" %d", tree[i]);
}
}
printf("\n");
}
return 0;
}



