一:学习总结
1.知识点关键词
栈:
- 栈是一种特殊的线性表。其特殊性在于限定插入和删除数据元素的操作只能在线性表的一端进行。
- 操作特点:先进后出。
- 由于于栈的插入和删除操作具有它的特殊性,所以用顺序存储结构表示的栈并不存在插入删除数据元素时需要移动的问题,但栈容量难以扩充的弱点仍就没有摆脱。
队列:
- 队列也是一种运算受限的线性表,它的运算限制与栈不同,是两头都有限制,插入只能在表的一端进行(只进不出),而删除只能在表的另一端进行(只出不进),允许删除的一端称为队尾,允许插入的一端称为队头 。
- 操作特点:先进先出。
逻辑结构:
- 简单说,逻辑结构就是数据之间的关系。大致可以分为两种:线性结构和非线性结构(集合、树、网)。
- 线性结构:有且只有一个开始结点和一个终端结点,并且所有结点都最多只有一个直接前驱和一个直接后继。例如:线性表,典型的线性表有:顺序表、链表、栈(顺序栈、链栈)和队列(顺序队列、链队列)。它们共同的特点就是数据之间的线性关系,除了头结点和尾结点之外,每个结点都有唯一的前驱和唯一的后继,也就是所谓的一对一的关系。
- 非线性结构:对应于线性结构,非线性结构也就是每个结点可以有不止一个直接前驱和直接后继。常见的非线性结构包括:树(二叉树)、图(网)等。
存储结构:
- 逻辑结构指的是数据间的关系,而存储结构是逻辑结构的存储映像。常见的存储结构有顺序存储、链式存储。
- 顺序存储:把逻辑上相邻的节点存储在物理位置上相邻的存储单元中,结点之间的逻辑关系由存储单元的邻接关系来体现。由此得到的存储结构为顺序存储结构,通常顺序存储结构是借助于数组来描述的。优点:节省空间,可以实现随机存取;缺点:插入、删除时需要移动元素,效率低。
- 链式存储:在计算机中用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。特点是元素在物理上可以不相邻,所以每个数据元素包括了一个数据域和一个指针域,数据域用来存放数据,而指针域用来指向其后继结点的位置。优点:插入、删除灵活;缺点:不能随机存取,查找速度慢。
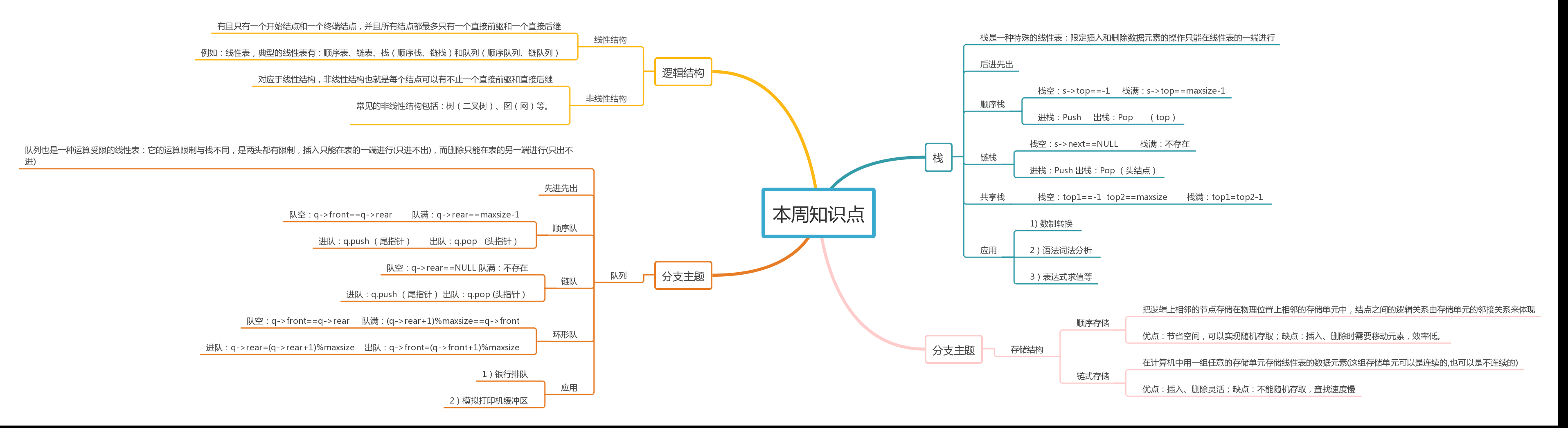
2.思维导图组织关键词。
二:PTA实验作业
题目1:报数游戏
1.设计思路
//主函数
cin>>总人数n>>规定退出的位次m
if n<m
“error”结束;
else
number:输出报到m的退出次序
//number函数
初始化队列q1
while !q1.empty() do
for i=0 to i=m-1 do
出队列,进队尾;
出队,输出;
if q1.size()<m do
依次输出队中所有元素
2.代码截图

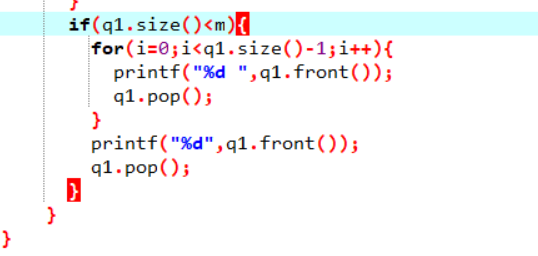
3.PTA提交列表说明

- 编译错误:在PTA中提交时编译器未选择C++
- 部分正确:没有考虑到总人数比较小时的情况,先判断一下总人数是否大于规定的退出位次
题目2:字符串是否对称
设计思路
字符串数组str[MAX]
创建栈S
cin>>str
Push(S,str)
Compare S和str
// Compare
for i=0 to i=S->MaxSize/2 do
if str[i]不等于栈顶元素 do
no,结束循环;
S->Top减一;
if 对称 do
yes
代码截图
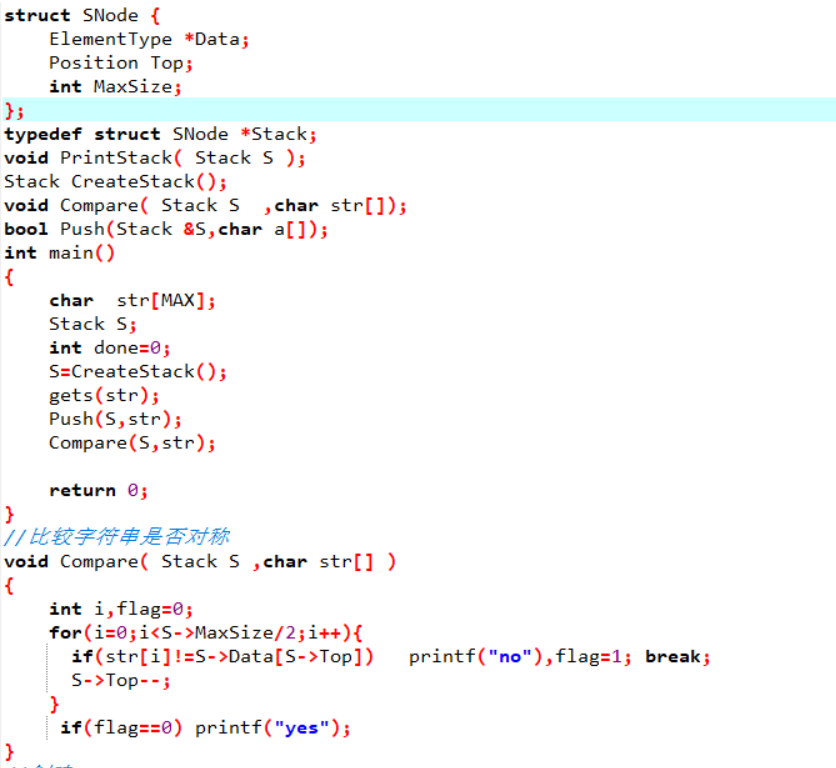
PTA提交列表说明。

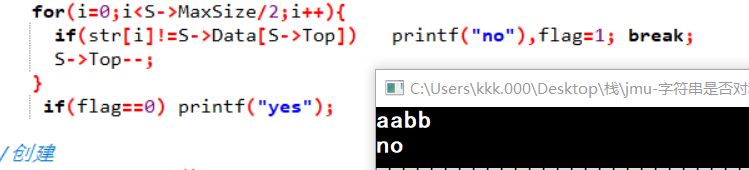
- 部分正确:最后输出时忘记加flag判断,导致不对称时既输出了no又输出yes

修改后:
题目3:银行业务队列简单模拟
1.设计思路
业务处理完成人数count=0;
cin>>顾客总人数n;
初始化队列:奇数进qA,偶数进qB;
L=qA.size();
while count<n do
if qA出队列的个数=L do
for i=0 to i=1 do
qA出队列,进队列;count++;
if !qB.empty()且count<n do
qB出队列,进qA;
输出qA;
//把处理过的顾客按顺序放入qA//
2.代码截图

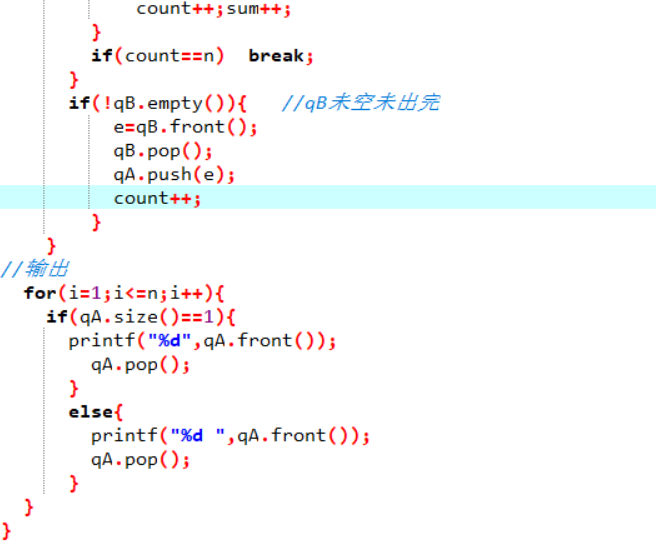
3.PTA提交列表说明。


- 答案错误:没有考虑到奇数比偶数少时,qA已经不需要再出队列进队列了,只要一直处理qB就好了


修改后:

所以这个情况就是在出队列A的地方没有考虑到qB比较多的情况;
- 部分正确:最大值没有取好。
看完其他同学的代码后发现自己把这道题做的有点复杂,应该可以把处理完的顾客直接输出,而不是再弄到队列中,这个样子反而要判断更多情况;只是我刚开始没有办法处理输出的格式,所以为了方便最后的输出才重新放回队列中。
三:截图本周题目集的PTA最后排名
1. 栈PTA排名:

2. 队列PTA排名:
3. 我的总分:200
四:阅读代码
代码:
#include <iostream>
#include <queue>
using namespace std;
void print_Triangle(int n){
queue<int>q;
for(int i=0;i<2*n-1;i++) //控制输出,美观
cout<<" ";
cout<<1<<" "<<endl; //输出第一行的1
q.push(1);
int s1,s2;
for(int i=2;i<=n;i++){
for(int k=0;k<2*n-i;k++) //控制输出,美观
cout<<" ";
s1 = 0;
for(int j=1;j<=i-1;j++){
s2 = q.front();
q.pop(); //出队
cout<<s1+s2<<" ";
q.push(s1+s2);
s1 = s2; //s1保留的是前一个数
}
cout<<1<<endl; //输出每行最后一个1
q.push(1);
}
}
int main(){
int n;
cin>>n; //输入要得到的杨辉三角的行数
print_Triangle(n);
return 0;
}
代码功能:输出打印杨辉三角(队列实现及数组递推实现)
优点:通过队列,将输出的数字保存入队,因为后面的数字需要用到前面的数字和的运算。第一行的1是默认直接入队输出的,每行的最后一个1也是默认输出的,它与前面的数字没有关系。其他的数字可以通过队头元素和下一个元素之和求得。注意第一个元素是通过上面的1和在其左边添一个0得到的。
代码相关地址:https://blog.csdn.net/jaster_wisdom/article/details/51532866
五:代码Git提交记录截图



