一.作业题目
实验题目:
试仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 (有理数是其分子、分母均为整数且分母不为零的分数)。
有理数基本运算如下所示:
1.构造有理数T,元素e1,e2分别被赋以分子、分母值
2.销毁有理数T
3.用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4.将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5.有理数T1,T2相加,结果存入有理数T3
6.有理数T1,T2相减,结果存入有理数T3
7.有理数T1,T2相乘,结果存入有理数T3
8.有理数T1,T2相除,结果存入有理数T3
二、博客作业要求:
1.作业内容:
用ADT的抽象数据模型描述你的有理数数据类型。
ADT Rational
{ 数据对象:D={e1,e2|e1,e2属于ElemType类型}
数据关系:R={<e1,e2>|e1是有理数的分子部分,e2是有理数的分母部分}
基本操作:
InitRat(&T,f1,f2)//构造有理数T,元素e1,e2分别被赋分v1,v2的值
DestoryRat(&T)//T被销毁
Get(*T,i,&e)//用e返回T的第i元的值
Modify(&T,i,e)//修改T的第i元为e
Redu(&T)//有理数的化简。
Add(*T1,*T2,&T3)//用T3返回两个有理数的和。
subt(*T1,*T2,&T3)//用T3返回两个有理数的差。
Mult(*T1,*T2,&T3)//用T3返回两个有理数的积。
Division(*T1,*T2,&T3)//用T3返回两个有理数的商。
}ADT Rational
2.数据结构、函数说明:
头文件
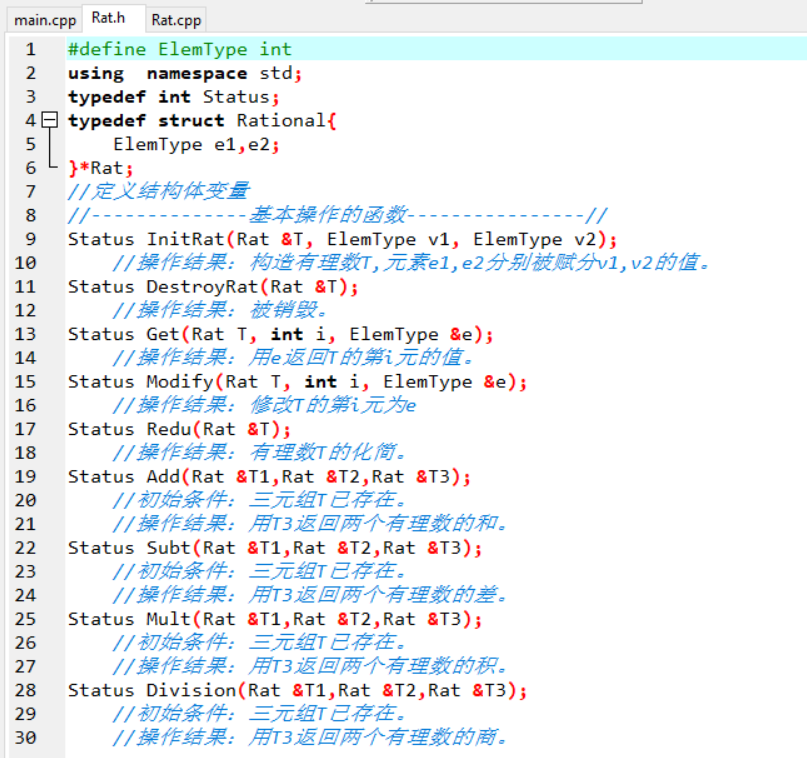
3.代码实现说明
构造函数

销毁

返回

修改
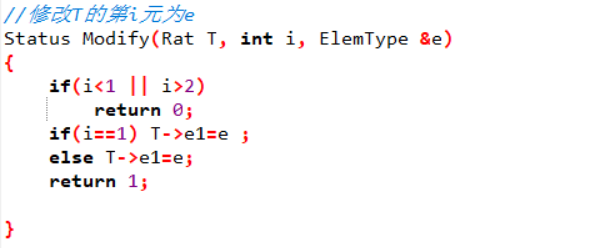
化简

求和

求差

求积

求商

主函数

5.结果展示
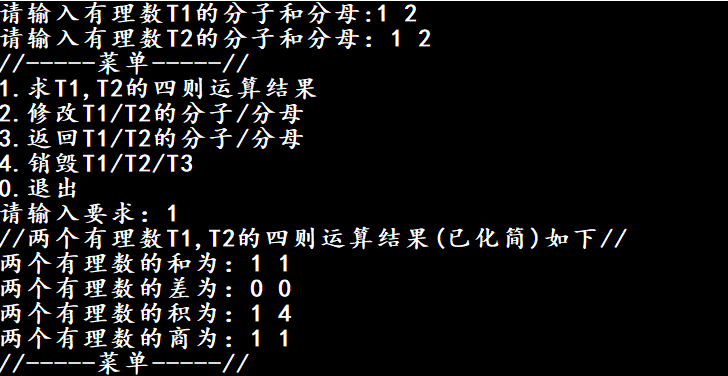
正常输入时:
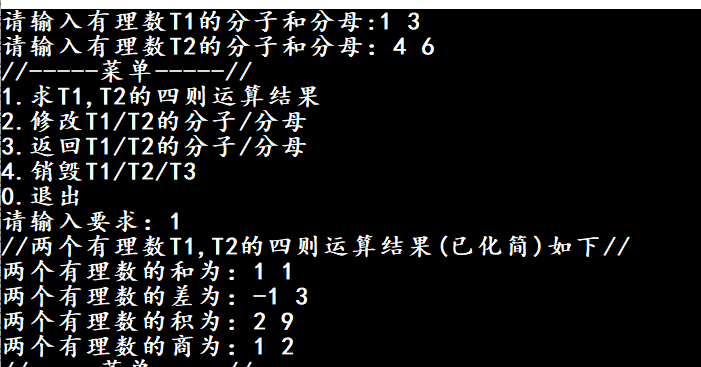
分母为零或负数时:

//直接输出提示,重新输入合法数据
分子为零:

计算特殊的商:
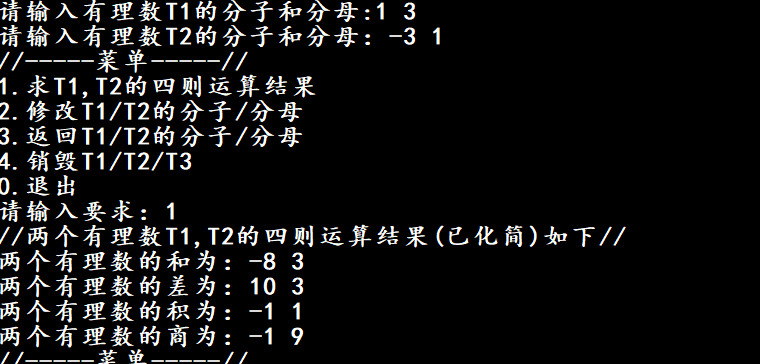
//T2分子为负数

//T2分子为零
计算结果化简:
修改

//把T2修改成1/3,并重新进行四则运算
6.总结
作业小结:
刚开始写没有思路,不知道要用什么来写,先是用数组,后来又改成了结构体;不清楚自己的错误,而且没有意识到空间申请的重要性;怕是要在数据结构上多下功夫才可以了。
知识点:
- 数据结构
数据结构是相互之间存在一种或多种特定关系的数据元素的集合。它包括元素集合和元素间关系;为了更好地管理未来要面对的大量数据,就需要把它们按照一定的方式组织起来,力求找到处理的最优化算法方式。 - 抽象数据类型
可以关心它的逻辑特征,不了解它的存储方式,同样不必要关心它如何存储。
ADT 抽象数据类型名{
数据对象:<数据对象的定义>
数据关系:<数据关系的定义>
基本操作:<基本操作的定义>
}ADT 抽象数据类型名

