【读书笔记】具体数学第一章

今天终于下定决心开始认真看具体数学这本书了，为以后啃 TAOCP 做好准备。陆陆续续会写一些读书笔记，记录下阅读过程中的一些心得。

 

好！现在开始正题，今天看完了第一章，才刚开始，已经感觉到Knuth的不同寻常。

 

第一章主要用递归解决了3个著名问题：汉诺塔、直线划分平面以及约瑟夫环。

 

汉诺塔(THE TOWER OF HANOI)

汉诺塔是一个古老的问题，已经被无数人研究过，还延伸出许多变体。具体定义可见这里。

作者在处理汉诺塔问题时已显现出极强的严谨性。令为最少所需的移动步数，作者证明了的上界和下界均为，并由此得到递推公式：

这在其他对于汉诺塔问题的处理中是较为少见的（作者自己竟也这么说=。=)

对于上界的证明比较显然，主要方法就是采用了递归思想提出一种移动的策略。即先将个小盘移到中间的一根空柱上，再将最大的放在目标柱子上，最后将个小盘移到目标柱上。

而对于下界的证明则较为tricky，作者巧妙的利用了规则中“较大的盘子不能放在较小的盘子下“这一点，证明了这步移动是必须的。具体的证明如下：

公式中的1，即移动一次最大的盘子，显然是必须的。对于剩下的步，即移动2次n-1个较小的盘，为什么是必须的呢？可以这样来解释：由于大盘不能放在小盘之上且每次只能移动最上面的盘子，当最大的盘子可以移动时，剩下的n-1个盘子一定在同一根柱子上（想想这是为啥），而这至少需要步。同样，要将剩下的n-1个盘子再放回最大的盘之上，还是至少需要步完成。

直线划分平面(LINES IN THE PLANE)

这也是一个比较有名的问题，可能初中或者高中就接触过，说的是n条直线最多可以将平面划分成多少个区域。作者同样用递归处理了这个问题并得出公式

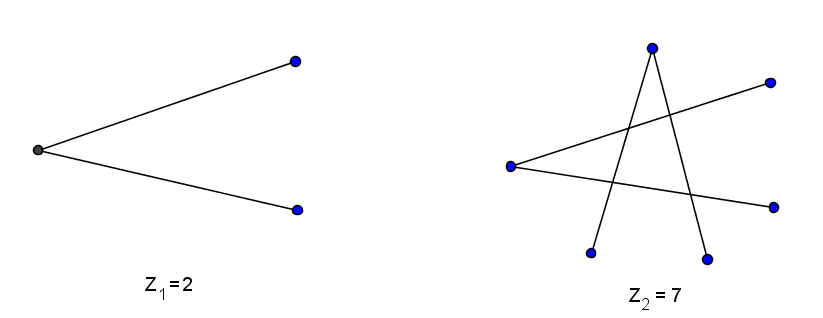
这一节比较有趣的是作者提出了一个变体问题：如果把直线换成带有一处弯折的折线（如下图），答案又会是什么？回答思路十分巧妙。（未完待续）