博客作业06--图
1.学习总结(2分)
1.1图的思维导图
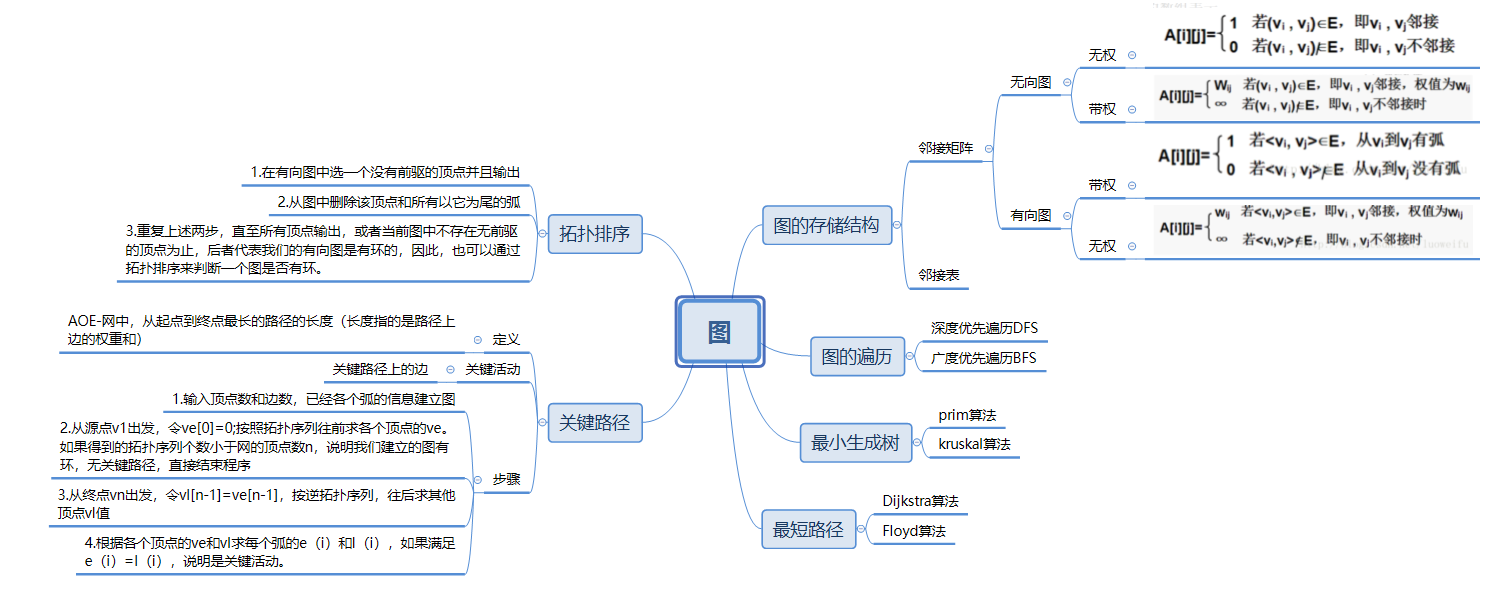
1.2 图结构学习体会
谈谈你对图结构中的几个经典算法学习体会。具体有:
1.深度遍历算法
深度遍历理解起来还是比较好理解的,但是翻译成代码,却有点困难,基本上是照搬课本上的代码,其实最重要的是理解递归的思想,然后就是些代码的基本套路了,多读基本就能理解了。
2.广度遍历算法
广度遍历与深度遍历基本上是同一个模板的东西,只是不同于递归而是用了队列,跟树的遍历基本差不多,学习来比深度简单,但是代码要更多。
3.Prim和Kruscal算法
这两种算法都是生成最小二叉树的方法,这两种方法的基本思想能理解,就是从待选的边中找最小的边加入,但是代码实现的话,只用过prim算法,跟着课本些的,想了很久才理解了代码的实现,而且不知道课本上的代码有什么问题,pta的一道题中有一个点始终过不了,后来网上找了另一中prim算法,才过了,而Kruscal算法则没有用代码实现过,还是有点生疏。
4.Dijkstra算法
写这个算法的时候,发现其实根prim算法有点相似,都是初始化,找最小,更新,这种思路往下写的,不过特别的一点是,可以找到整条路径,但是思路也都差不多。
5.拓扑排序算法
这个算法就相对前面的算法相对简单,思路好理解,代码实现的话,有了前面的基础,写起来也是相对较简单的。
2.PTA实验作业(4分)
题目1:7-1 图着色问题
设计思路(伪代码或流程图)
主函数:
定义一个int类型的set s
输入图节点数,边数和颜色数
用creatMGraph建一个图
输入待检测的涂色方案数v
for i=0 to v
输入涂色方案
清空set
通过放到set的颜色数比较是否正确
if(set中的颜色数正确)
通过Judge函数判断涂色方案是否正确
if(返回1)输出yes
else 输出no
else
输出no
end
Judge函数:
for i=0 to n
for j=0 to n
if(矩阵中存有边)
if(边两个端点的颜色一样)
返回0
end
end
返回1
代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
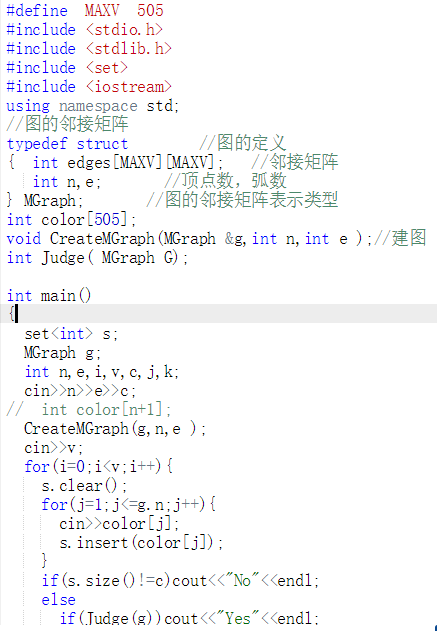
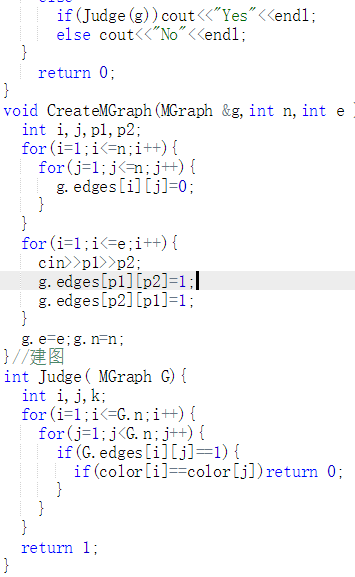
PTA提交列表说明。
刚开始打算用邻接表做,写了好久,刚开始是MAXV的值设置的太小,导致运行错误,后来没有考虑到联通图与非联通图的判断,后来慢慢改只能如果就差一个卡DFS不重复访问顶点的错误实在是不懂什么意思,问了同学,他说使用邻接矩阵做的,没遇到这个错误,而且更简单,于是我干脆直接全改成了矩阵,花了一会而就都过了。
题目2:7-3 六度空间
设计思路(伪代码或流程图)
主函数:
输入节点数,边数建一个图
遍历每一个节点
用BFS函数计算每个节点距离不超过6的结点数
节点数出总数,输出
BFS函数:
定义数组visited存节点是否遍历
定义队列q
定义last存每层的最后一个节点
last初始等于待计算的节点v
初始visited数组
visited【v】=1,表示v已访问过
v入队
while(队列不空)
取出队首元素
for i=1 to n
if(该元素未访问且跟i有边)
入队
visited数组中该元素标记为已访问
cnt++
定义tail记录最后存入队列的元素
end
if(v==last)
level++
更新last等于last
if(level等于6)结束循环
end
返回cnt
代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
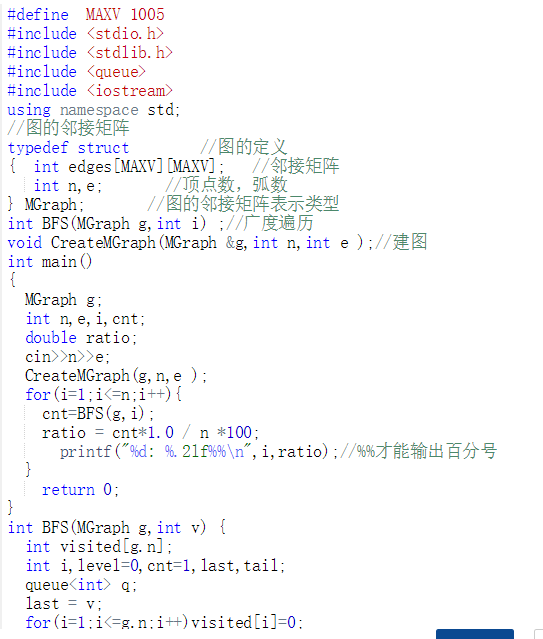


PTA提交列表说明。
这道题理解了思路后就会发现还是挺好做的,但是不清楚MAX的值才会提交了好多次。
题目3:7-6 修建道路
设计思路(伪代码或流程图)
主函数:
输入n建立矩阵
通过矩阵建图
输入v
for i=0 to v
输入两个端点
在邻接矩阵中把原来的边数变成1
end
调用Prim函数返回最小的生成树边的值
输出生成树的减v
Prim:
定义lowcost数组和closest数组
初始化这两个数组
for j=2 to n
找最小的边数
存下最小边数和节点
end
cnt+=min,way++
更新lowcost数组和closest数组
返回cnt
代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)


PTA提交列表说明。
刚开始完全找不到思路怎么写,后来写了一个版本出来,结果只对了一个点,后来就完全找不到错误要怎么改,当时思路太乱,根本不知道怎么改。后来在舍友哪里听到了这个题目的类似取巧的方法,具体就是将已经修建的道路权值改写为1,所以在计算时权值为1的路就会作为最小的路径计算进去,只要到最后减掉修建的路数就可以,结果写了一下就对了。
3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名(截图带自己名字的排名)
3.2 我的总分:310
4. 阅读代码(必做,1分)
图的最短路径问题-Floyd算法-07-图4 哈利·波特的考试
哈利·波特要考试了,他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha,将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念,例如ahah可以将老鼠变成猫。另外,如果想把猫变成鱼,可以通过念一个直接魔咒lalala,也可以将猫变老鼠、老鼠变鱼的魔咒连起来念:hahahehe。
现在哈利·波特的手里有一本教材,里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场,要考察他把这只动物变成任意一只指定动物的本事。于是他来问你:带什么动物去可以让最难变的那种动物(即该动物变为哈利·波特自己带去的动物所需要的魔咒最长)需要的魔咒最短?例如:如果只有猫、鼠、鱼,则显然哈利·波特应该带鼠去,因为鼠变成另外两种动物都只需要念4个字符;而如果带猫去,则至少需要念6个字符才能把猫变成鱼;同理,带鱼去也不是最好的选择。
输入格式:
输入说明:输入第1行给出两个正整数N (≤100)和M,其中N是考试涉及的动物总数,M是用于直接变形的魔咒条数。为简单起见,我们将动物按1~N编号。随后M行,每行给出了3个正整数,分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100),数字之间用空格分隔。
输出格式:
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度,中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的,则输出0。如果有若干只动物都可以备选,则输出编号最小的那只。
输入样例:
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
输出样例:
4 70
#include<iostream>
using namespace std;
#define INFINITY 123456
#define MAXN 101
int Graph[MAXN][MAXN];
int dist[MAXN][MAXN];
int N,M;
//Floyd算法求最短路径
void Flody()
{
int k,i,j;
for(k=1; k<=N; k++){
for(i=1; i<=N; i++){
for(j=1; j<=N; j++){
if(dist[i][k] + dist[k][j] < dist[i][j]){
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("hali.txt","r",stdin);
#endif
int i, j, x, y, weight;
scanf("%d%d", &N, &M);
//初始化图数组
for(i=1; i<=N; i++){
for(j=1; j<=N; j++){
if(i == j) Graph[i][j] = 0;
else Graph[i][j] = INFINITY;
}
}
//读取数据
for(i=1; i<=M; i++){
scanf("%d%d%d", &x, &y, &weight);
Graph[x][y] = weight;
Graph[y][x] = weight;
}
//初始化距离数组
for(i=1; i<=N; i++){
for(j=1; j<=N; j++){
dist[i][j] = Graph[i][j];
}
}
Flody();
int minAnimal = -1, minDist = INFINITY;
for(i=1; i<=N; i++){
int tmp = 0;
for(j=1; j<=N; j++){
if(dist[i][j] > tmp) tmp = dist[i][j];
}
if(tmp == INFINITY){
printf("0\n");
return 0;
}
//printf("%d\n",i);
if(tmp < minDist){
minAnimal = i;
minDist = tmp;
}
}
printf("%d %d\n", minAnimal, minDist);
return 0;
}
题目看起来特别的复杂,但是如果把动物看成图的顶点,魔咒的长度看成是顶点之间的权重的话,那么题目就变成了。求最短路径问题了。
这题用的是弗洛伊德算法来计算最短路径的问题,主干函数也就只有几行的代码,简单明了,值得借鉴。





