一. 逻辑回归
1.背景:使用逻辑回归预测学生是否会被大学录取。
2.首先对数据进行可视化,代码如下:
pos = find(y==1); %找到通过学生的序号向量 neg = find(y==0); %找到未通过学生的序号向量 plot(X(pos,1),X(pos,2),'k+','LineWidth',2,'MarkerSize',7); %使用+绘制通过学生 hold on; plot(X(neg,1),X(neg,2),'ko','MarkerFaceColor','y','MarkerSize',7); %使用o绘制未通过学生 % Put some labels hold on; % Labels and Legend xlabel('Exam 1 score') ylabel('Exam 2 score') % Specified in plot order legend('Admitted', 'Not admitted') hold off;
3.sigmoid函数的实现,代码如下:![]()
function g = sigmoid(z) %函数文件名为sigmoid.m %SIGMOID Compute sigmoid function % g = SIGMOID(z) computes the sigmoid of z. % You need to return the following variables correctly g = zeros(size(z)); temp=-z; temp=e.^temp; temp=temp+1; temp=1./temp; g=temp; end
4.代价函数的实现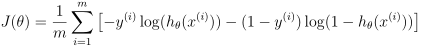 代码如下:
代码如下:
function [J, grad] = costFunction(theta, X, y) %函数名文件名为costFunction.m m = length(y); % number of training examples % You need to return the following variables correctly J = 1/m*(-(y')*log(sigmoid(X*theta))-(1-y)'*log(1-sigmoid(X*theta))); %计算代价函数 grad = zeros(size(theta)); grad = 1/m*X'*(sigmoid(X*theta)-y); %求梯度
end
5.代替梯度下降的优化方法fminunc(),代码如下:
% 参数GradObj设置为on表示,通知函数fminunc()我们的代价函数costFunction()可以返回代价值和梯度值,函数fminunc()可以直接使用梯度值进行计算 options = optimset('GradObj', 'on', 'MaxIter', 400); % Run fminunc to obtain the optimal theta % This function will return theta and the cost [theta, cost] = ... fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);
6.使用计算出的θi值做预测,预测函数如下:
function p = predict(theta, X) m = size(X, 1); % Number of training examples p = zeros(m, 1); p=floor(sigmoid(X*theta).*2); %因为使用了floor()函数,所以函数值要扩大二倍
二. 正规化逻辑回归
1.特征映射(Feature Mapping):使用两个特征(x1,x2)组合出更多的特征如x1x2,x12,x22等。代码如下:
function out = mapFeature(X1, X2) degree = 6; out = ones(size(X1(:,1))); for i = 1:degree for j = 0:i out(:, end+1) = (X1.^(i-j)).*(X2.^j); %一共生成27项 end
end
end
2.计算在逻辑回归中经过正规化的代价函数和梯度:
function [J, grad] = costFunctionReg(theta, X, y, lambda) m = length(y); % number of training examples
J = 1/m*(-(y')*log(sigmoid(X*theta))-(1-y)'*log(1-sigmoid(X*theta)))+(1/(2*m))*lambda*(sum(theta .^2) - theta(1)^2); %正规化时不用对θ1正规化 grad = zeros(size(theta) grad = 1/m*X'*(sigmoid(X*theta)-y)+lambda*theta/m; grad(1) = grad(1)-lambda*theta(1)/m; end



