KNN-K近邻算法(1)
KNN(K-nearest neighbors)
- 思想简单
- 数学所需知识少（近零）
- 效果好
- 可解释机器学习算法使用过程中的很多细节问题
- 更完整的刻画机器学习应用的流程
- 天然可解决多分类问题
- 可解决回归问题
K近邻本质：如果两个样本足够相似，那么它们就有可能属于同一类别。
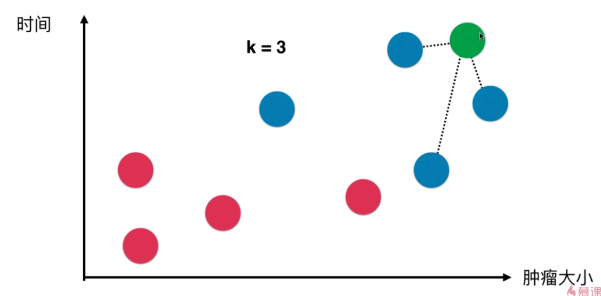
e.g. 绿色的点是新加入的点，取其最近的k（3）个点作为小团体来投票，票数高的获胜（蓝比红-3：0）,所以绿点应该也是蓝点
计算距离：
最常见 -> 欧拉距离，求a, b两点的距离（二维，三维，多维）：
-> 
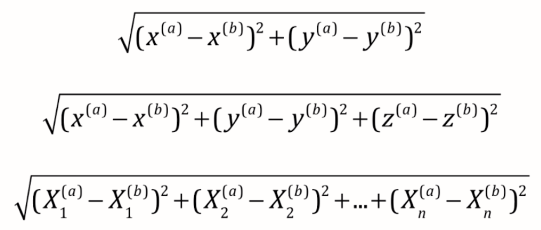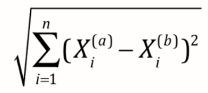
理解小笔记：(（a样本第一个维度特征-b样本第一个维度特征）2 + （a样本第二个维度特征-b样本第二个维度特征）2 + ... ) 再开根
近乎可以说，KNN算法是机器学习中唯一一个不需要训练过程的算法。输入用例可直接送给训练数据集。
- KNN可以被认为是没有模型的算法
- 为和其他算法统一，可认为其训练数据集本身就是模型
使用KNN解决回归问题
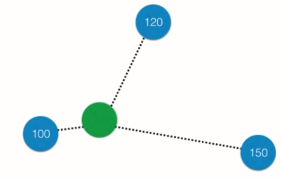
绿点的值即可设为离它最近的三个点的（加权）平均值
KNN缺点
最大缺点：效率低下。
如果训练集有m个样本，n个特征，则预测每一个新的数据，都需要计算它与每一个点之间的距离(共m个点)，每计算一个点的距离就需要O(n)的时间复杂度。
每预测一个，共需要O(m*n)的时间复杂度。
优化，使用树的结构：KD-Tree， Ball-Tree
缺点2：高度数据相关
尽管所有的机器学习算法都是根据给定的数据集来学习，都是高度数据相关的。但KNN相对而言对outlier更加敏感。例如加入使用k=3，当预测点旁有两个错误数据就足以导致预测结果的错误。
缺点3：预测结果不具有可解释性
往往实际应用中我们只知道结果是什么是不够的，我们需要知道为什么是这样的结果从而得到某种规律可以进行推广。
缺点4：维数灾难
随维度的增加，“看似相近”的两个点之间的距离越来越大
解决方法：降维
超参数
指在算法运行前需要决定的参数。
与之相对的模型参数指：算法过程中学习的参数。
KNN算法中没有模型参数，其中K是典型的超参数。
寻找好的超参数：
- 领域知识
- 经验数值
- 实验搜索：尝试测试几组不同的超参数，找到最好的配对
KNN中的其他超参数？ -> 距离权重
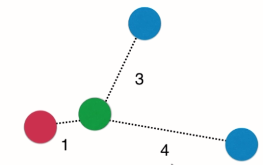
权重一般取距离的倒数。
考虑距离权重的另一个好处：可解决平票问题
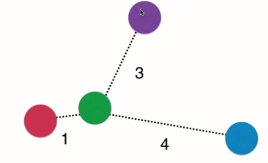
不考虑距离时，红蓝紫平票，模型会随机选一个颜色作为输出结果。但很明显这是不合理的（滑稽脸）。而加入距离权重后，则小红获胜（合情合理有理有据）。
更多的距离定义
之前说到的距离都是欧拉距离。还有一种常见的距离叫曼哈顿距离。
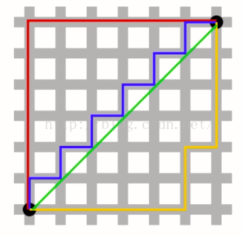
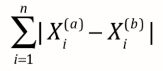
定义为：两点在每个维度上距离的和。如上图例子中黑色两点的曼哈顿距离即它两在x方向上的差值加上y方向上的差值。所有彩线的曼哈顿距离都相同（其中绿线即欧拉距离）
推广一下可发现：
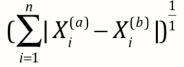-> 曼哈顿距离
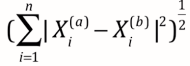-> 欧拉距离
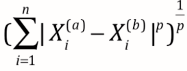-> 明可夫斯基距离Minkowski distance
当p=1时，明可是曼哈顿距离，p=2时，变身成曼哈顿距离，p=其他数，其他距离的表示方式。
【系统提示】叮咚！又获得一个新的超参数，p
由sklearn中叫metric的超参数控制，默认为明可夫斯基距离
- 向量空间余弦相似度 Cosine Similarity
- 调整余弦相似度 Adjusted Cosine Similarity
- 皮尔森相关系数 Pearson Correlation Coefficient
- Jaccard相似系数 Jaccard Coefficient
