303. 区域和检索 - 数组不可变，307. 区域和检索 - 数组可修改（线段树）

介绍

线段树的题目，起步基本就是hard。

其实线段树就是一种经典空间换时间，用一维度的空间降了一维度的时间。当然，使用线段树也要满足一些条件，即数据的组织结构要有特点。

一个不错的讲解可以看：https://www.acwing.com/blog/content/3369/

 

线段树之所以称为“树”，是因为其具有树的结构特性。线段树由于本身是专门用来处理区间问题的（包括 RMQRMQ 、 RSQRSQ) 问题等。

 

 

 

 

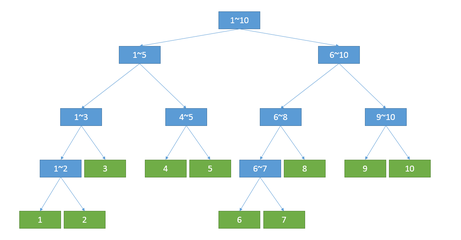
对于每一个子节点而言，都表示整个序列中的一段子区间；对于每个叶子节点而言，都表示序列中的单个元素信息；子节点不断向自己的父亲节点传递信息，而父节点存储的信息则是他的每一个子节点信息的整合。

线段树就是分块思想的树化，或者说是对于信息处理的二进制化——用于达到 O(logn)级别的处理速度， log以 2为底。而分块的思想，则是可以用一句话总结为：通过将整个序列分为有穷个小块，对于要查询的一段区间，总是可以整合成 k 个所分块与 m 个单个元素的信息的并 (0<=k,m<=sqrt(n))(0<=k,m<=n​) 。但普通的分块不能高效率地解决很多问题，所以作为 log级别的数据结构，线段树应运而生。

 

如果你只是想像力扣303和307题解给个ac的答案，那么这两题其实也没必要去做了，其实这两题本质应该是练习线段树。

leetcode303区域和检索 - 数组不可变，如下：

给定一个整数数组  nums，处理以下类型的多个查询:

1. 计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的 和 ，其中 left <= right

实现 NumArray 类：

• NumArray(int[] nums) 使用数组 nums 初始化对象
• int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )

 

示例 1：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) 
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

其实本题就是线段树的模板。主要是线段树的建立和查询。

class NumArray {
public:
    struct node
    {

        int sum=0;
        long long left=-999;
        long long right=-999;
       
   
    }newnums[1000000];

    vector<int> seq;
    int ans=0;
    void build(int i,int left,int right)
    {
        newnums[i].left=left;
        newnums[i].right=right;
        if(left==right)
        {
             newnums[i].sum=seq[left];
            return;
        }
        int mid=(left+right)/2;
        build(i*2,left,mid);
        build(i*2+1,mid+1,right);
        newnums[i].sum=newnums[i*2+1].sum+newnums[i*2].sum;
    }
    void findsum(int k,int i,int j)
    {
       if(newnums[k].left>=i&&newnums[k].right<=j) 
       {
          // cout<<newnums[k].sum<<endl;
           ans+=newnums[k].sum;
           return;
       }
       int mid=(newnums[k].left+newnums[k].right)>>1;
       if(i<=mid) findsum(k*2,i,j);
       if(j>mid) findsum(k*2+1,i,j);
    }

    NumArray(vector<int>& nums) {
          seq.push_back(0);
          for(int i=0;i<nums.size();i++)
          {
              seq.push_back(nums[i]);
          }
       if(nums.size()!=0)build(1,1,nums.size());
    }
    
    int sumRange(int i, int j) {
          findsum(1,i+1,j+1);
        int final=ans;
        ans=0;
        return final;
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(i,j);
 */
 

 

leetcode307. 区域和检索 - 数组可修改，如下：

给你一个数组 nums ，请你完成两类查询。

1. 其中一类查询要求 更新 数组 nums 下标对应的值
2. 另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 ，其中 left <= right

实现 NumArray 类：

• NumArray(int[] nums) 用整数数组 nums 初始化对象
• void update(int index, int val) 将 nums[index] 的值 更新 为 val
• int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 （即，nums[left] + nums[left + 1], ..., nums[right]）

 

示例 1：

输入：
["NumArray", "sumRange", "update", "sumRange"]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
输出：
[null, 9, null, 8]

解释：
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // 返回 1 + 3 + 5 = 9
numArray.update(1, 2);   // nums = [1,2,5]
numArray.sumRange(0, 2); // 返回 1 + 2 + 5 = 8


线段树的建立  线段树的修改模板题。

class NumArray {
public:
    struct node
    {

        int sum=0;
        long long left=-999;
        long long right=-999;
       
   
    }newnums[100000];

    vector<int> seq;
    int ans=0;
    void build(int i,int left,int right)
    {
        newnums[i].left=left;
        newnums[i].right=right;
        if(left==right)
        {
             newnums[i].sum=seq[left];
            return;
        }
        int mid=(left+right)/2;
        build(i*2,left,mid);
        build(i*2+1,mid+1,right);
        newnums[i].sum=newnums[i*2+1].sum+newnums[i*2].sum;
    }
    void findsum(int k,int i,int j)
    {
       if(newnums[k].left>=i&&newnums[k].right<=j) 
       {
          // cout<<newnums[k].sum<<endl;
           ans+=newnums[k].sum;
           return;
       }
       int mid=(newnums[k].left+newnums[k].right)>>1;
       if(i<=mid) findsum(k*2,i,j);
       if(j>mid) findsum(k*2+1,i,j);
    }
    void change(int origin,int i,int val)
    {
         if(newnums[i].left==newnums[i].right)
        {
            newnums[i].sum=val;
            return;
        }
        int mid=(newnums[i].left+newnums[i].right)/2;
        if(origin<=mid) change(origin,i*2,val);
        else change(origin,i*2+1,val);
        newnums[i].sum=newnums[i*2].sum+newnums[i*2+1].sum;
    }
    NumArray(vector<int>& nums) {
          seq.push_back(0);
          for(int i=0;i<nums.size();i++)
          {
              seq.push_back(nums[i]);
          }
       if(nums.size()!=0)build(1,1,nums.size());
    }
    
    void update(int i,int val)
    {
       change(i+1,1,val);

    }
    int sumRange(int i, int j) {
          findsum(1,i+1,j+1);
        int final=ans;
        ans=0;
        return final;
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(i,j);
 */