c++ stl nth_element 原理解析

　　nth_element是stl中的一个库函数，该函数可以从某个序列中找到第 n 小的元素 K，并将 K 移动到序列中第 n 的位置处。不仅如此，整个序列经过 nth_element() 函数处理后，所有位于 K 之前的元素都比 K 小，所有位于 K 之后的元素都比 K 大。

但这个函数与完整排序的区别在于：

　　1.它只关注第n个，只保证小于该值的元素在其左边，大于等于的在其右边，但并不保证其完全有序。

　　2.它的时间复杂度在O(N),而许多排序所用的复杂度为O(NlogN)。对于特定的找到第k大数的问题，所花时间是好于排序的。

 

它的原理思想如图

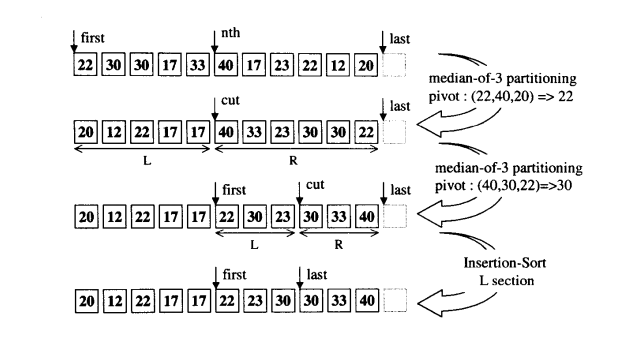
　　这个算法的思路很像快排中partation函数。首先有一个first ,nth,last，首先找到这三个所在位置值的中位数，这里22，40，20中位数为22。

　　然后对于22进行第一轮，方法同partation，22则作为锚点。

　　然后这里找到右端的第一个(如果是数组为0-10装着上图的值)，这里右端第一个即数组下标为5的数字40，而传入我们要找的nth也为5(其实即找到0-10中第6大的数)，因此其小于等于右端起点，于是进入右段进行下一轮。

　　下一轮同理40,30,22取30 进行交换使cut两端被分割。

　　这时候再右端第一个和nth再进入，这时判断到子序列已经不大于3了，直接用插入排序。最后即得到第nth（这里传入nth为5，实际即第六大的数）为22.

 

以下是代码的解析：

下面是nth_element在本人电脑中stl的源码(可以跳过)

template<typename _RandomAccessIterator, typename _Compare>
    inline void
    nth_element(_RandomAccessIterator __first, _RandomAccessIterator __nth,
        _RandomAccessIterator __last, _Compare __comp)
    {
      // concept requirements
      __glibcxx_function_requires(_Mutable_RandomAccessIteratorConcept<
                  _RandomAccessIterator>)
      __glibcxx_function_requires(_BinaryPredicateConcept<_Compare,
        typename iterator_traits<_RandomAccessIterator>::value_type,
        typename iterator_traits<_RandomAccessIterator>::value_type>)
      __glibcxx_requires_valid_range(__first, __nth);
      __glibcxx_requires_valid_range(__nth, __last);

      if (__first == __last || __nth == __last)
    return;

      std::__introselect(__first, __nth, __last,
             std::__lg(__last - __first) * 2,
             __gnu_cxx::__ops::__iter_comp_iter(__comp));
    }

 

其中直接讲其核心的__introselect函数部分

template<typename _RandomAccessIterator, typename _Size, typename _Compare>
    void
    __introselect(_RandomAccessIterator __first, _RandomAccessIterator __nth,
          _RandomAccessIterator __last, _Size __depth_limit,
          _Compare __comp)
    {
      while (__last - __first > 3)
    {
      if (__depth_limit == 0)
        {
          std::__heap_select(__first, __nth + 1, __last, __comp);
          // Place the nth largest element in its final position.
          std::iter_swap(__first, __nth);
          return;
        }
      --__depth_limit;                                               
      _RandomAccessIterator __cut =      
        std::__unguarded_partition_pivot(__first, __last, __comp); //这里函数返回的是分割后右段的第一个元素。后面会详细讲解一下这个的功能
      if (__cut <= __nth)  //如果右段起点小于等于nth 
        __first = __cut;   //进入右段，对右段进行下次的分割
      else
        __last = __cut;
    }
      std::__insertion_sort(__first, __last, __comp);
    }

这个算法的思路很像快排中partation函数的思路。但对于段长度在3时候，就选择使用插入排序。

 

这里的关键是__unguarded_partition_pivot函数部分

 template<typename _RandomAccessIterator, typename _Compare>
    inline _RandomAccessIterator
    __unguarded_partition_pivot(_RandomAccessIterator __first,
                _RandomAccessIterator __last, _Compare __comp)
    {
      _RandomAccessIterator __mid = __first + (__last - __first) / 2;  
      std::__move_median_to_first(__first, __first + 1, __mid, __last - 1,    //对first last mid排序找到中位值
                  __comp);                                                    //这里的中位值即下面的pivot点
      return std::__unguarded_partition(__first + 1, __last, __first, __comp);  //这里即实现了对于类似快排若左边大于pivot则与右边小于pivot的交换
    }                                                                           //并返回的是右端第一个