【leetcode】Weekly Contest 94

　　题目不难，被第二题卡了半个多小时QAQ，另一个就是以后能用Hashmap和Hashset的绝不遍历。

1. Leaf-Similar Trees

 

　　dfs、层次遍历把叶子节点遍历然后对比即可，只要是先遍历左节点后遍历右节点就行。

class Solution {
    public boolean leafSimilar(TreeNode root1, TreeNode root2) {
        ArrayList<Integer> res1 = new ArrayList<>();
        ArrayList<Integer> res2 = new ArrayList<>();
        getLeaf(root1, res1);
        getLeaf(root2, res2);
        boolean equal = true;
        if(res1.size() == res2.size()){//叶子节点数量都不一样就不可能一样
            int i;
            for(i = 0;i<res1.size();i++){
                if(res1.get(i) != res2.get(i)){
                    equal = false;
                    break;
                }
            }
        }
        return equal;
    }
    
    void getLeaf(TreeNode root,ArrayList<Integer> res){//先序遍历获得所有叶子节点
        if(root == null){
            return ;
        }
        if(root.left == null && root.right ==null){
            res.add(root.val);
        }
        getLeaf(root.left, res);
        getLeaf(root.right, res);
    }
}

874. Walking Robot Simulation

　　被这题卡了好久，一开始想写的是判断起始点到末尾点中间是否有障碍物，前进的终点位置是最近的那个障碍物前一个位置，后来意识到前进的距离最多是9，直接一个点一个点判断就好了，这样可以直接用Hashset找是否有那个点。

    public static int robotSim(int[] commands, int[][] obstacles) {
        int[][] dir = {{0,1},{1,0},{0,-1},{-1,0}};
        int nowdir = 0;//当前方向
        int x = 0,y = 0;//记录当前位置
        int max = 0;
        int nx,ny;//下一个位置
        Set<Long> obstacleSet = new HashSet();
        for (int[] obstacle: obstacles) {
            long ox = (long) obstacle[0];
            long oy = (long) obstacle[1];
            obstacleSet.add((ox << 16) + oy);//前16位记录x的位置，后16位记录y的位置
        }
        
        for(int i = 0;i<commands.length;i++){
            if(commands[i] == -1){
                nowdir = (nowdir+1)%4;
            }else if (commands[i] == -2) {
                nowdir = (nowdir-1+4)%4;
            }else {
                for (int k = 0; k < commands[i]; ++k) {
                    nx = x + dir[nowdir][0];
                    ny = y + dir[nowdir][1];
                    long code = (((long) nx) << 16) + ((long) ny );
                    if (!obstacleSet.contains(code)) {
                        x = nx;
                        y = ny;
                        max = Math.max(max, x*x + y*y);
                    }
                }
            }
        }
        return max;
    }

875. Koko Eating Bananas

　　第三题不难，二分查找K的值（1-10^9），每次判断时间是否小于H即可，时间复杂度o(10^4*log10^9)。

class Solution {
    public int minEatingSpeed(int[] piles, int H) {
        int up = 0;
        for (int i : piles) {//记录最大的数量，每小时吃的肯定不需要大于这个数量
            up = Math.max(up, i);
        }
        return find(piles,H,1,up);
    }
    
    static int find(int[] piles, int H,int min,int max){//二分搜索
        if(min == max){
            return min;
        }else{
            int mid = (min+max)/2;
            // System.out.println(min +" "+ max+" "+mid);
            if(eatAll(piles, H, mid)){//能吃完，就尝试更小的（当然mid也可能是所求值）
                return find(piles, H, min, mid);
            }else {//吃不完，就每小时吃多点
                return find(piles, H, mid+1, max);
            }
        }
    }
    
    static boolean eatAll(int[] piles,int H,int K){
        int need = 0;
        for (int i : piles) {
            need+=(i/K)+((i%K)==0?0:1);
        }
        return need<=H;
    }
}

873. Length of Longest Fibonacci Subsequence

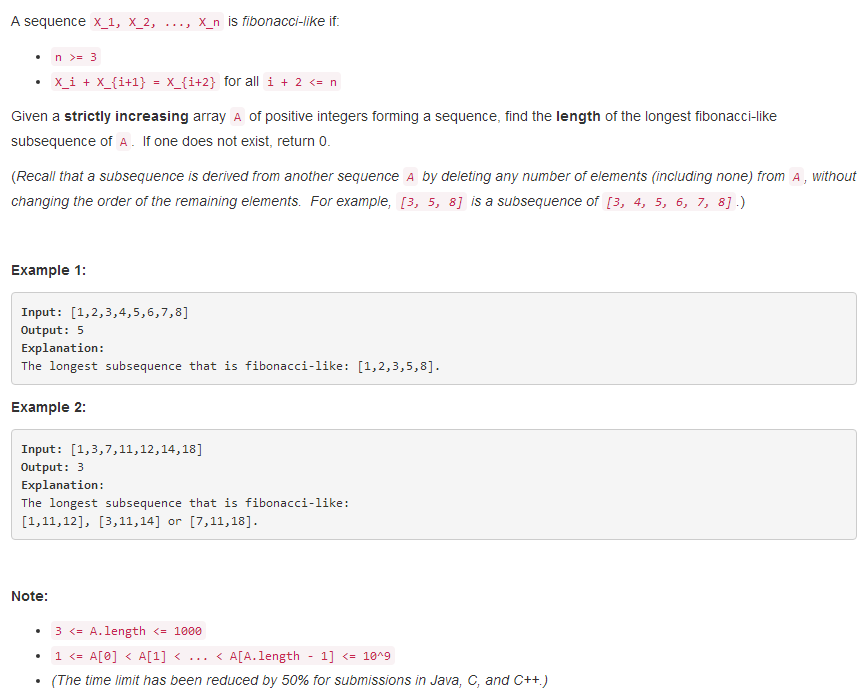
　　这题思路对了，用二位数组dp[i][j]记录以A[i]为倒数第二个点，A[j]为最后一个点的最大斐波那契数列长度，o（n^2）遍历这个二维数组填充数据，再遍历一次取得结果即可。

class Solution {
    public int lenLongestFibSubseq(int[] A) {
        int dp[][] = new int[A.length][A.length];
        HashMap<Integer, Integer> index = new HashMap<>();//记录数组值的下标
        for(int i = 0;i<A.length;i++){
            index.put(A[i], i);
        }
        for(int i = 2;i<A.length;i++){
            for(int j = 0;j<i;j++){
                Integer k = index.get(A[i] - A[j]);//查看是否存在需要的值
                if(k!=null && k<j){
                    dp[i][j] = Math.max(dp[i][j], dp[j][k]+1);
                }
            }
        }
        int res = 0;
        for (int[] is : dp) {
            for (int i : is) {
                res = Math.max(res, i);
            }
        }
        return res==0?0:res+2;
    }
}

　　一开始没用Hashmap记录，因此需要第三个循环搜索是否存在需要的值，然后就tle惹，用Hashmap降了一个时间复杂度。

　　本次题目都不是特别难，不过还是仰望那些20分钟AK的大佬（我看题目的时间可能都不止20min QAQ）。