斜率优化
Preface
斜率优化就是用来优化 \(DP\) 的,由于之前太弱,以及网上各种假题解,一直没看懂,这篇博客就写一下自己的理解吧
BZOJ1597: [Usaco2008 Mar]土地购买
Description
农夫John准备扩大他的农场,他正在考虑N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <= 1,000,000; 1 <= 长 <= 1,000,000). 每块土地的价格是它的面积,但FJ可以同时购买多快土地. 这些土地的价格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3x5的地和一块5x3的地,则他需要付5x5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.
Solution
由于是斜率优化第一次写,写得详细些
记土地长、宽分别为 \(x\),\(y\)
首先,根据题意,如果一块大的土地可以完全包含一块小的土地,那么小的土地就不必考虑了,直接去掉。可以通过以 \(x\) 为第一关键字, \(y\) 为第二关键字从小到大排序,扫一遍即可得出。
接下来,可以发现去掉小土地后的序列满足 \(x\) 单调递增,\(y\) 单调递减。
设前 \(i\) 块土地的最小花费为 \(dp[i]\),可以得到一个 \(DP\) 方程:
这个方程时间复杂度为 \(O(n^2)\) 过不掉的。
现在我们考虑当前走到了 \(t\) 的位置,对于 \(a<b<t\),我们考虑什么时候从 \(a\) 转移到 \(t\) 比从 \(b\) 转移到 \(t\) 更优。
显然,满足下式时更优:
所以(注意不等式的符号与 \(y\) 的单调性,这很重要):
这时我们令 \(K(a,b)=\frac{dp[a]-dp[b]}{y[a+1]-y[b+1]}\),那么当 \(K(a,b)<-x[t]\) 且 \(a<b\) 时,对决策点 \(t\) 而言, \(a\) 比 \(b\) 优。
有这个结论就可以搞事了。
考虑以下两个条件:
1.对于两个点 \(a,b\) 满足 \(a<b<t\) 且 \(K(a,b)\geq -x[t]\) 那么 \(b\) 优于 \(a\) ,而 \(x[t]\) 单调递增, \(-x[t]\) 单调递减,所以对于 \(t_0\geq t\) 而言,均有 \(K(a,b)\geq -x[t_0]\)。换言之,对于以后的决策,都不可能从 \(a\) 转移更优。
2.假设对于三个点 \(a,b,c\) 满足 \(a<b<c<t\) 且 \(K(a,b)<K(b,c)\)
---2.(1)\(K(b,c)>-x[t]\) 时, \(c\) 比 \(b\) 优,故不选 \(b\)
---2.(2)\(K(b,c)<-x[t]\) 即 \(K(a,b)<K(b,c)<-x[t]\) 时,\(a\) 优于 \(b\) 优于 \(c\),还是不会选 \(b\)
所以说我们维护的可行转移必须满足\(a<b<c<t\) 且 \(K(a,b)>K(b,c)\)
如果非要把 \(K(a,b)\) 看做斜率的话,那我们维护的可行转移点集应该是一个上凸壳
算法的具体流程:
维护一个双端队列,每次到一个决策点 \(t\) 都检查队首两个元素,如果\(a<b<t\) 且 \(K(a,b)\geq -x[t]\),就把队首元素弹出,直到只剩一个元素或者不满足 \(K(a,b)\geq -x[t]\);
然后,由于 \(K\) 单调递减,可以发现队首元素就是最优转移,利用这个转移计算 \(dp[t]\);
再然后将 \(t\) 插入队列,插入时如果K(队尾,队尾第二个)<K(队尾,t)就弹出队尾元素,直到只剩一个元素或者或者K(队尾,队尾第二个)>K(队尾,t)。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 50000+9;
int n;
struct PAIR{
LL x,y;
}num[MAXN],val[MAXN];
int tot;
LL dp[MAXN];
bool cmp(const PAIR &A,const PAIR &B){
if(A.x==B.x)
return A.y<B.y;
return A.x<B.x;
}
double K(int a,int b){
return 1.0*(dp[a]-dp[b])/(val[a+1].y-val[b+1].y);
}
void solve(){
int head=1,tail=2;
static int que[MAXN];
for(int i=1;i<=tot;i++){
while(tail-head>1 && K(que[head],que[head+1])>=-val[i].x)
head++;
dp[i]=dp[que[head]]+val[i].x*val[que[head]+1].y;
while(tail-head>1 && K(que[tail-1],que[tail-2])<K(que[tail-1],i))
tail--;
que[tail++]=i;
}
printf("%lld\n",dp[tot]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld%lld",&num[i].x,&num[i].y);
sort(num+1,num+n+1,cmp);
for(int i=1;i<=n;i++){
if(num[i].y<=num[i+1].y)continue;
while(tot && val[tot].y<=num[i].y)
tot--;
val[++tot]=num[i];
}
solve();
return 0;
}
BZOJ1010: [HNOI2008]玩具装箱toy
Description
P教授要去看奥运,但是他舍不下他的玩具,于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩,其可以将任意物品变成一堆,再放到一种特殊的一维容器中。P教授有编号为1...N的N件玩具,第i件玩具经过压缩后变成一维长度为Ci.为了方便整理,P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具,那么两件玩具之间要加入一个单位长度的填充物,形式地说如果将第i件玩具到第j个玩具放到一个容器中,那么容器的长度将为 \(x=j-i+\sum C_k\) ( \(i<=K<=j\))
制作容器的费用与容器的长度有关,根据教授研究,如果容器长度为x,其制作费用为(X-L)^2.其中L是一个常量。P教授不关心容器的数目,他可以制作出任意长度的容
器,甚至超过L。但他希望费用最小.
Input
第一行输入两个整数N,L.接下来N行输入Ci.1<=N<=50000,1<=L,Ci<=10^7
Output
输出最小费用
Solution
下面的题就简写了
将每件物品长度+1,L++。(自己推一下式子就发现为什么了了)
求物品长度前缀和记为 \(sum\)
朴素动规方程:
像上一题一样推式子
对于 \(a<b<t\),当满足
时, \(a\) 优于 \(b\)
此时
经检验,满足之前所说的两个条件
这次 \(K\) 单调递增,是个下凸壳
同样注意队首的弹出。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 50000+9;
int n,L;
int num[MAXN];
LL sum[MAXN];
LL dp[MAXN];
double K(int a,int b){
return 1.0*(dp[a]-dp[b])/(sum[a]-sum[b])+1.0*(sum[a]+sum[b]);
}
void solve(){
static int head=1,tail=2;
static int que[MAXN];
for(int i=1;i<=n;i++){
while(tail-head>1 && K(que[head],que[head+1])<=2*(sum[i]-L))
head++;
dp[i]=dp[que[head]]+(sum[i]-sum[que[head]]-L)*(sum[i]-sum[que[head]]-L);
while(tail-head>1 && K(que[tail-1],que[tail-2])>K(que[tail-1],i))
tail--;
que[tail++]=i;
}
printf("%lld\n",dp[n]);
}
int main(){
scanf("%d%d",&n,&L);
L++;
for(int i=1;i<=n;i++){
scanf("%d",&num[i]);
num[i]++;
}
for(int i=1;i<=n;i++)
sum[i]=sum[i-1]+num[i];
solve();
return 0;
}
BZOJ1096: [ZJOI2007]仓库建设
Description
L公司有N个工厂,由高到底分布在一座山上。如图所示,工厂1在山顶,工厂N在山脚。由于这座山处于高原内陆地区(干燥少雨),L公司一般把产品直接堆放在露天,以节省费用。突然有一天,L公司的总裁L先生接到气象部门的电话,被告知三天之后将有一场暴雨,于是L先生决定紧急在某些工厂建立一些仓库以免产品被淋坏。由于地形的不同,在不同工厂建立仓库的费用可能是不同的。第i个工厂目前已有成品Pi件,在第i个工厂位置建立仓库
的费用是Ci。对于没有建立仓库的工厂,其产品应被运往其他的仓库进行储藏,而由于L公司产品的对外销售处设置在山脚的工厂N,故产品只能往山下运(即只能运往编号更大的工厂的仓库),当然运送产品也是需要费用的,假设一件产品运送1个单位距离的费用是1。假设建立的仓库容量都都是足够大的,可以容下所有的产品。你将得到以下数据:1:工厂i距离工厂1的距离Xi(其中X1=0);2:工厂i目前已有成品数量Pi;:3:在工厂i建立仓库的费用
Ci;请你帮助L公司寻找一个仓库建设的方案,使得总的费用(建造费用+运输费用)最小。
Input
第一行包含一个整数N,表示工厂的个数。接下来N行每行包含两个整数Xi, Pi, Ci, 意义如题中所述。
Output
仅包含一个整数,为可以找到最优方案的费用。
【数据规模】
对于100%的数据, N ≤1000000。 所有的Xi, Pi, Ci均在32位带符号整数以内,保证中间计算结果不超过64位带符号整数。
Solution
将 \(dis\) 记为工厂到山脚的距离
\(succ\) 为后缀加权和,即 \(succ[t]=\sum_{i=t}^{n}P[i]*dis[i]\)
\(sum\) 为 \(P\) 的前缀和
朴素动规方程(\(dp[i]\)表示 \(i\) 处设有仓库):
对于 \(a<b<t\) ,\(a\) 优于 \(b\) 当且仅当
满足两个条件,是个上凸壳
BZOJ1911: [Apio2010]特别行动队
Description



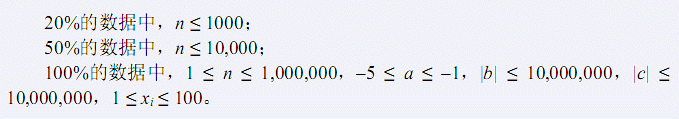
Solution
\(sum\) 为 \(x\) 的前缀和
朴素动规方程(\(dp[i]\)表示 \(i\) 处为一个行动队的结束位置):
对于 \(x<y<t\) ,若 \(x\) 比 \(y\) 优,则:
满足两个条件,是一个上凸壳
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 1000000+9;
typedef long long LL;
int n;
LL a,b,c;
LL sum[MAXN];
LL dp[MAXN];
LL square(LL x){
return x*x;
}
double K(int x,int y){
return 1.0*(dp[x]-dp[y])/(sum[x]-sum[y])-1.0*b+1.0*a*(sum[x]+sum[y]);
}
void solve(){
static int head=1,tail=2;
static int que[MAXN];
//que[head]=0;
for(int i=1;i<=n;i++){
while(tail-head>1 && K(que[head],que[head+1])>=2*a*sum[i])
head++;
LL val=sum[i]-sum[que[head]];
dp[i]=dp[que[head]]+a*square(val)+b*val+c;
while(tail-head>1 && K(que[tail-1],que[tail-2])<K(que[tail-1],i))
tail--;
que[tail++]=i;
}
printf("%lld\n",dp[n]);
}
int main(){
scanf("%d",&n);
scanf("%lld%lld%lld",&a,&b,&c);
for(int i=1;i<=n;i++){
LL x;
scanf("%lld",&x);
sum[i]=sum[i-1]+x;
}
solve();
return 0;
}
BZOJ4518: [Sdoi2016]征途
Description
Pine开始了从S地到T地的征途。
从S地到T地的路可以划分成n段,相邻两段路的分界点设有休息站。
Pine计划用m天到达T地。除第m天外,每一天晚上Pine都必须在休息站过夜。所以,一段路必须在同一天中走完。
Pine希望每一天走的路长度尽可能相近,所以他希望每一天走的路的长度的方差尽可能小。
帮助Pine求出最小方差是多少。
设方差是v,可以证明,v×m2是一个整数。为了避免精度误差,输出结果时输出v×m2。
Input
第一行两个数 n、m。
第二行 n 个数,表示 n 段路的长度
Output
一个数,最小方差乘以 m^2 后的值
HINT
1≤n≤3000,保证从 S 到 T 的总路程不超过 30000
Solution
方差公式:\(s^2=\frac{1}{m}\sum(x_i-\overline{x})^2\)
题目中让结果乘上 \(m^2\) 显然有玄机
问题变为了求\(\sum x_i^2\) 的最小值,其中 \(x_i\) 是原序列的一段和
设 \(dp[i][j]\) 表示当前已经选了 \(j\) 个连续的段,其中最后一个段的结尾是 \(i\)
朴素动规方程:
时间复杂度\(O(n^3)\)
和之前的套路一样,对于 \(a<b<t\),若 \(a\) 优于 \(b\),则
满足两个条件,是个下凸包。
斜率优化后时间复杂度为 \(O(n)\)
这一题需要注意初始化,dp[i][5]=sum[i]^2,直接转移应该有问题,会从dp[i][0]进行瞎转移,似乎有问题。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 3000+9;
typedef long long LL;
int n,m;
LL sum[MAXN];
LL dp[MAXN][MAXN];
LL square(LL x){
return x*x;
}
double K(int a,int b,int step){
return 1.0*(dp[a][step]-dp[b][step])/(sum[a]-sum[b])+1.0*(sum[a]+sum[b]);
}
void solve(){
static int head=1,tail=2;
static int que[MAXN];
for(int i=1;i<=n;i++)
dp[i][6]=square(sum[i]);
for(int j=2;j<=m;j++){
head=1,tail=2;
for(int i=1;i<=n;i++){
while(tail-head>1 && K(que[head],que[head+1],j-1)<=2*sum[i])
head++;
dp[i][j]=dp[que[head]][j-1]+square((sum[i]-sum[que[head]]));
while(tail-head>1 && K(que[tail-1],que[tail-2],j-1)>K(que[tail-1],i,j-1))
tail--;
que[tail++]=i;
}
}
printf("%lld\n",dp[n][m]*m-square(sum[n]));
}
int main(){
freopen("in.in","r",stdin);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
LL x;
scanf("%lld",&x);
sum[i]=sum[i-1]+x;
}
solve();
return 0;
}
BZOJ3675: [Apio2014]序列分割
Description
小H最近迷上了一个分隔序列的游戏。在这个游戏里,小H需要将一个长度为n的非负整数序列分割成k+1个非空的子序列。为了得到k+1个子序列,小H需要重复k次以下的步骤:
1.小H首先选择一个长度超过1的序列(一开始小H只有一个长度为n的序列——也就是一开始得到的整个序列);
2.选择一个位置,并通过这个位置将这个序列分割成连续的两个非空的新序列。
每次进行上述步骤之后,小H将会得到一定的分数。这个分数为两个新序列中元素和的乘积。小H希望选择一种最佳的分割方式,使得k轮之后,小H的总得分最大。
Input
输入第一行包含两个整数n,k(k+1≤n)。
第二行包含n个非负整数a1,a2,...,an(0≤ai≤10^4),表示一开始小H得到的序列。
Output
输出第一行包含一个整数,为小H可以得到的最大分数。
Sample Input
7 3
4 1 3 4 0 2 3
Sample Output
108
HINT
【样例说明】
在样例中,小H可以通过如下3轮操作得到108分:
1.-开始小H有一个序列(4,1,3,4,0,2,3)。小H选择在第1个数之后的位置将序列分成两部分,并得到4×(1+3+4+0+2+3)=52分。
2.这一轮开始时小H有两个序列:(4),(1,3,4,0,2,3)。小H选择在第3个数字之后的位置将第二个序列分成两部分,并得到(1+3)×(4+0+2+3)=36分。
3.这一轮开始时小H有三个序列:(4),(1,3),(4,0,2,3)。小H选择在第5个数字之后的位置将第三个序列分成两部分,并得到(4+0)×(2+3)= 20分。
经过上述三轮操作,小H将会得到四个子序列:(4),(1,3),(4,0),(2,3)并总共得到52+36+20=108分。
【数据规模与评分】
数据满足2≤n≤100000,1≤k≤min(n -1,200)。
Solution
就方程而言,这和上一题类似,好像还简单一些。
记 \(dp[i][j]\) 为前 \(i\) 个数已经分为 \(j\) 部份。
朴素动规方程:
时间复杂度达到了 \(O(n^2k)\)
考虑 \(a<b<t\),若 \(a\) 比 \(b\) 优,则:
满足两个条件,是个下凸壳
优化后时间复杂度可以达到 \(O(nk)\)
这题有两个坑点:
- 由于 \(sum[b]-sum[a]\) 可以是 \(0\) ,所以要么把分母乘过去(
太麻烦了),或者像我一样特判返回INF至于为什么,只要考虑 \(sum[b]-sum[a]=0\) 时,K(que[head],que[head+1],opt^1)<=sum[i],必须是false。 - 这题卡空间,要用滚动数组
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 100000+9;
typedef long long LL;
const LL INF = 1000000000000LL;
LL sum[MAXN];
LL dp[MAXN][7];
int n,k;
double K(int a,int b,int step){
if(sum[a]==sum[b])
return INF;
return 1.0*(dp[a][step]-dp[b][step])/(sum[b]-sum[a])+1.0*(sum[a]+sum[b]);
}
void solve(){
static int head=1,tail=2;
static int que[MAXN];
int opt=0;
for(int j=1;j<=k;j++){
opt^=1;
head=1,tail=2;
for(int i=1;i<=n;i++)
dp[i][opt]=0;
for(int i=1;i<=n;i++){
while(tail-head>1 && K(que[head],que[head+1],opt^1)<=sum[i])
head++;
dp[i][opt]=dp[que[head]][opt^1]+sum[que[head]]*(sum[i]-sum[que[head]]);
while(tail-head>1 && K(que[tail-1],que[tail-2],opt^1)>K(que[tail-1],i,opt^1))
tail--;
que[tail++]=i;
}
}
printf("%lld\n",dp[n][opt]);
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++){
LL x;
scanf("%lld",&x);
sum[i]=sum[i-1]+x;
}
solve();
return 0;
}
BZOJ3156: 防御准备
Description

Input
第一行为一个整数N表示战线的总长度。
第二行N个整数,第i个整数表示在位置i放置守卫塔的花费Ai。
Output
共一个整数,表示最小的战线花费值。
HINT
1<=N<=106,1<=Ai<=109
Solution
写出朴素方程考虑优化即可。
我感觉已经不用写了,代码里其实很清楚。方程和斜率都能看出来,套路都一样
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 1000000+9;
typedef long long LL;
int n;
int num[MAXN];
LL dp[MAXN];
double K(int a,int b){
return 2.0*(dp[a]-dp[b])/(a-b)+a+b+1;
}
void solve(){
static int head=1,tail=2;
static int que[MAXN];
for(int i=1;i<=n;i++){
while(tail-head>1 && K(que[head],que[head+1])<=2*i)
head++;
dp[i]=dp[que[head]]+1LL*(i-que[head]-1)*(i-que[head])/2+num[i];
while(tail-head>1 && K(que[tail-1],que[tail-2])>K(que[tail-1],i))
tail--;
que[tail++]=i;
}
printf("%lld\n",dp[n]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&i[num]);
solve();
return 0;
}
BZOJ3437: 小P的牧场
Description
小P在MC里有n个牧场,自西向东呈一字形排列(自西向东用1…n编号),于是他就烦恼了:为了控制这n个牧场,他需要在某些牧场上面建立控制站,每个牧场上只能建立一个控制站,每个控制站控制的牧场是它所在的牧场一直到它西边第一个控制站的所有牧场(它西边第一个控制站所在的牧场不被控制)(如果它西边不存在控制站,那么它控制西边所有的牧场),每个牧场被控制都需要一定的花费(毕竟在控制站到牧场间修建道路是需要资源的嘛~),而且该花费等于它到控制它的控制站之间的牧场数目(不包括自身,但包括控制站所在牧场)乘上该牧场的放养量,在第i个牧场建立控制站的花费是ai,每个牧场i的放养量是bi,理所当然,小P需要总花费最小,但是小P的智商有点不够用了,所以这个最小总花费就由你来算出啦。
Input
第一行一个整数 n 表示牧场数目
第二行包括n个整数,第i个整数表示ai
第三行包括n个整数,第i个整数表示bi
Output
只有一行,包括一个整数,表示最小花费
Sample Input
4
2 4 2 4
3 1 4 2
Sample Output
9
样例解释
选取牧场1,3,4建立控制站,最小费用为2+(2+1*1)+4=9。
Hint
1<=n<=1000000, 0 < a i ,bi < = 10000
Solution
和 BZOJ1096: [ZJOI2007]仓库建设 类似
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 1000000+9;
typedef long long LL;
int n;
LL a[MAXN],b[MAXN];
LL sum[MAXN],succ[MAXN];
LL dp[MAXN];
double K(int a,int b){
return 1.0*(dp[a]-dp[b]+succ[a+1]-succ[b+1])/(sum[a]-sum[b])+n;
}
void solve(){
static int head=1,tail=2;
static int que[MAXN];
for(int i=1;i<=n;i++){
while(tail-head>1 && K(que[head],que[head+1])<=i)
head++;
dp[i]=a[i]+dp[que[head]]+succ[que[head]+1]-succ[i+1]-1LL*(n-i)*(sum[i]-sum[que[head]]);
while(tail-head>1 && K(que[tail-1],que[tail-2])>K(que[tail-1],i))
tail--;
que[tail++]=i;
}
printf("%lld\n",dp[n]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
for(int i=1;i<=n;i++)
scanf("%lld",&b[i]);
for(int i=1;i<=n;i++)
sum[i]=sum[i-1]+b[i];
for(int i=n;i;i--)
succ[i]=succ[i+1]+(n-i)*b[i];
solve();
return 0;
}


