DIM中的一些知识点(慢更)

最大深度互信息模型(DIM)执行图片搜索器

1. MINE方法:
   之前看下面这句话的时候总是云里雾里,好好推了下公式终于明白啦。
   利用神经网络计算互信息可以转换为计算两个数据集合的联合分布和边缘分布之间的散度

   具体推导过程:
   

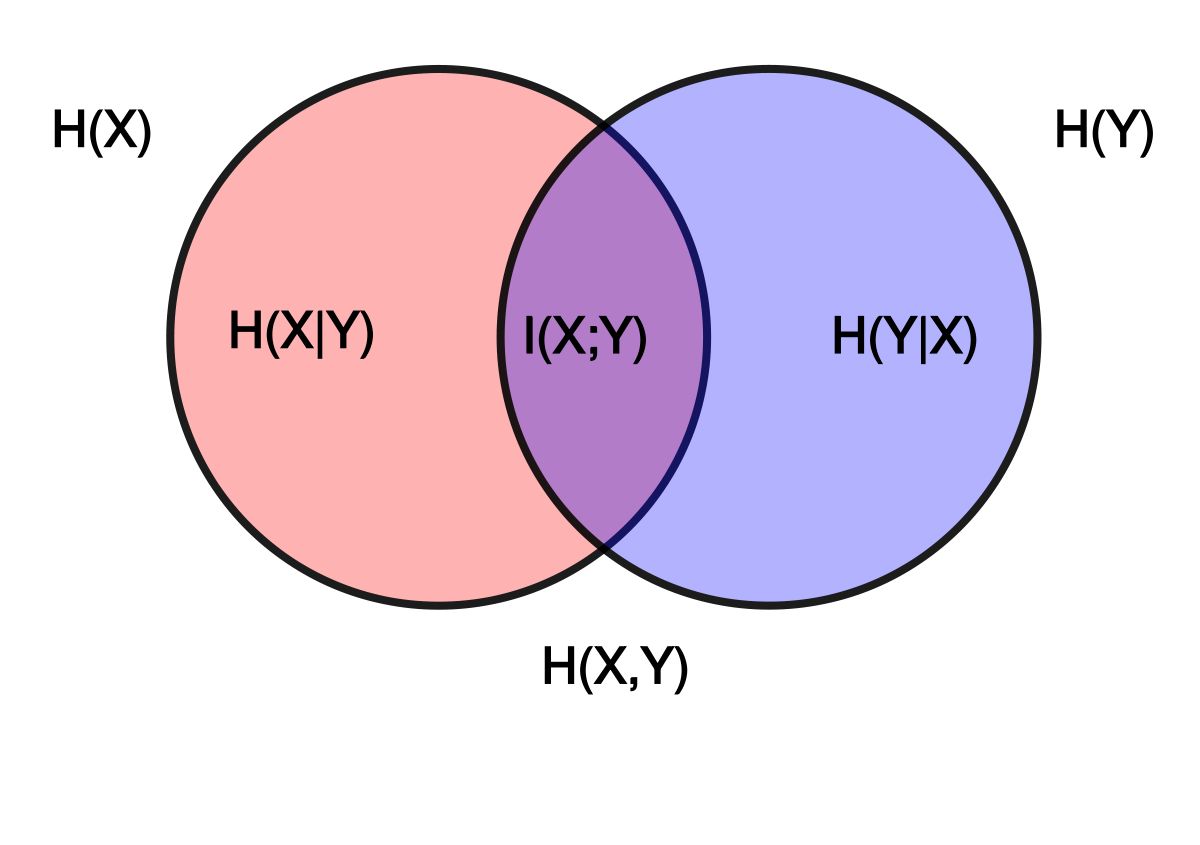
   如图,首先，我们有：

         I(X;Y) = H(X) - H(X|Y)
   

   其中，H(X|Y) 表示给定随机变量 Y 的条件下，随机变量 X 的条件熵。根据条件熵的定义，我们有：

       H(X|Y) = - sum_x sum_y P(x,y) log(P(x|y))
   

   将这个公式代入上面的公式中，我们得到：

     I(X;Y) = H(X) + sum_x sum_y P(x,y) log(P(x|y))
   

   根据概率论中的乘法规则，我们有 P(x,y) = P(x|y)P(y)，因此上面的公式可以写成：

     I(X;Y) = H(X) + sum_x sum_y P(x,y) log(P(x,y)/P(y))
   

   由于 H(X) = - sum_x P(x) log(P(x))，因此上面的公式可以写成：

   I(X;Y) = - sum_x P(x) log(P(x)) + sum_x sum_y P(x,y) log(P(x,y)/P(y))
   

   将上面的公式中的求和号用全概率公式 P(x)=sum_y P(x,y)拆开，我们得到：

   I(X;Y) = - sum_x sum_y P(x,y) log(P(x)) + sum_x sum_y P(x,y) log(P(x,y)/P(y))
   

   接下来，我们将上面的公式中的两个求和号合并成一个求和号，得到：

   I(X;Y)=sum_x sum_y P(x,y)(log(P(x,y))-log(P(x))-log(P(y)))
   

   根据对数函数的性质，我们有 log(a/b)=log(a)-log(b)，因此上面的公式可以写成：

   I(X;Y)=sum_x sum_y P(x,y)(log(P(x,y)/(P(x)*P(y))))
   

   根据 KL 散度的定义，我们有 D_KL(P||Q)=sum_x P(x)(log(P(x)/Q(x)))，因此上面的公式可以写成：

    I(X;Y)=D_KL(P(X,Y)||P(X)*P(Y))
   

   这就是互信息和 KL 散度之间的关系。