差分约束
update on 2020.5.5 欢迎来锤爆楼主,转载请标明地址
如果嫌我讲得不好那就来康康这篇吧传送门
其实就是一种最短路的模型
引例
给定n个变量和m个不等式,每个不等式形如 x[i] - x[j] <= a[k],求 x[n-1] - x[0] 的最大值。
(0 <= i, j < n)
例:n=4
\(x_1-x_0 <= 2\)①
\(x_2-x_0 <= 7\)②
\(x_3-x_0 <= 8\)③
\(x_2-x_1 <= 3\)④
\(x_3-x_2 <= 2\)⑤
然后经过认真的瞎搞计算就变成了这个鸭子:
1、③ \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x_3-x_0 <= 8\)
2、②+⑤\(\ \ \ \ \ \ \ \ \ \ \ \ x_3-x_0 <= 9\)
3、①+④+⑤\(\ \ \ \ \ \ \ x_3-x_0 <= 7\)
对于每个不等式 \(x_i - x_j <= a_k\),对结点 \(j\) 和 \(i\) 建立一条 \(j -> i\)的有向边,
边权为\(a_k\),求\(x_{n-1} - x_0\) 的最大值就是求 \(0\) 到\(n-1\)的最短路。
我们会发现这个东西移项之后有没有和spfa的松弛操作十分的相似(我也不知道是怎么看出来的)
spfa的松弛操作:
如果d[u] + w(u, v) < d[v],
则更新d[v] = d[u] + w(u, v);
然后再随便的瞎搞一下,就能把图画出来了...

正题(差分约束)
一、我们可以从数形结合的方式来看
从数形结合上看的定义如若一个系统由n个变量和m个不等式组成,并且这m个不等式对应的系数矩阵
中每一行有且仅有一个1和-1,其它的都为0,这样的系统称为差分约束( difference constraints )系统。
\(x_1-x_0 <= 2\)①
\(x_2-x_0 <= 7\)②
\(x_3-x_0 <= 8\)③
\(x_2-x_1 <= 3\)④
\(x_3-x_2 <= 2\)⑤
然后上边的一坨式子就可以变成一个每行只有一个1和-1其余都是0的矩阵
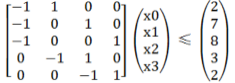
乱搞操作:
\(x[i] - x[j] <= a[k]\)
\(x[i] <= x[j] + a[k]\)
令\(a[k] = w(j, i)\), 则\(x[i] <= x[j] +w(j,i)\)
令\(i = v, j = u,d=x\)
\(d[v]<=d[u]+w(j,i)\)
SPFA中的一个松弛操作:
\(if(d[u] + w(u, v) < d[v]) \ \ \ \ \ d[v] = d[u] + w(u, v);\)
就是使\(d[u]+w(u,v)>=d[v] ;\)
对于每个不等式 x[i] - x[j] <= a[k],对结点 j 和 i 建立一条 j -> i的有向边,
边权为a[k],求x[n-1] - x[0] 的最大值就是求 0 到n-1的最短路。
二、可以从三角不等式上看
\(B-A <= c\)①
\(C - B <= a\)②
\(C-A <= b\)③
然后我们就可以转化成三角不等式上来了...
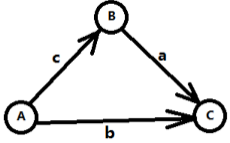
我们想要知道\(C - A\)的最大值,通过\(① + ②\),可以得到 \(C - A <= a + c\),
所以这个问题其实就是求\(min(b, a+c)\)
三角不等式推广到\(m\)个,变量推广为\(n\)个,就变成\(n\)个点\(m\)条边的最短路问题.
三、判断是否有解:
最短路,会出现负权圈或者根本就不可达的情况,所以在不等式组转化的图上也有可能出现上述情况
,差分约束系统的解有三种情况:
1、有解;
2、无解;
3、无限多解;
1、x[t]-x[s] 最大值不存在

因为里边有一个负环,所以就在环里边出不来了
2、x[4]-x[1] 最大值无限大
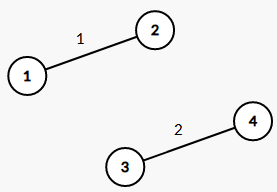
因为两边都不相连,然后你自己吧那个不等式写出来之后会发现,如果你约一下分,那么会出现一个恒等式
四、最小值问题
\(B-A <= c\)①
\(C - B <= a\)②
\(C-A <= b\)③
如果我们把不等式的符号改变一下那么求得最短路那不就是变成了最长路问题吗,
那么我们在做题的时候只需要把spfa中的松弛操作的符号变一下就行了....
五、不等式的标准化
1>如果给出的不等式有"<="也有">=" :
如果需要求的是两个变量差的最大值,那么需要将所有不等式转变成"\(<=\)"的形式,建图后求最短路;
相反,如果需要求的是两个变量差的最小值,那么需要将所有不等式转化成"\(>=\)",建图后求最长路。
2>如果有形如:A - B = c 这样的等式呢?
我们可以将它转化成以下两个不等式:
\(A - B >= c\) ①
$A - B <= c $ ②
再通过上面的方法将其中一种不等号反向,建图即可。
3>如果这些变量都是整数域上的,那么遇到A - B < c这样的不带等号的不等式怎么办呢?
我们可以将它转化成"\(<=\)"或者"\(>=\)"的形式,即 \(A - B <= c - 1\)形式就可以做了...
奉上几个练习题
一堆杂题
hdu 3592 World Exhibition $\ \ \ \ \ \ \ \ \ \ $ ★★☆☆☆ 题解 最短路模型 + 判负环
hdu 3440 House Man $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ ★★☆☆☆ 题解 最短路模型 + 判负环
poj 1364 King $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ ★★☆☆☆ 差分约束系统 - 最长路模型 + 判正环
poj 1932 XYZZY $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ ★★☆☆☆ 最长路 + 判正环
hdu 3666 THE MATRIX PROBLEM $\ $ ★★★☆☆ 差分约束系统 - 最长路模型 + 判正环
poj 2983 Is the Information Reliable? ★★★☆☆ 差分约束系统 - 最长路模型 + 判正环
poj 1752 Advertisement $\ \ \ \ \ \ \ \ \ \ \ \ \ \ $ ★★★☆☆ 限制较强的差分约束 - 可以贪心求解
hdu 1529 Cashier Employment $\ \ \ \ \ \ $ ★★★☆☆ 二分枚举 + 差分约束系统 - 最长路模型
hdu 1534 Schedule Problem $\ \ \ \ \ \ \ \ \ \ $★★★☆☆ 差分约束系统 - 最长路模型
ZOJ 2770 Burn the Linked Camp $\ \ \ $ ★★★☆☆
hdu 4109 Instrction Arrangement $\ \ \ \ $ ★★★☆☆



