CCS - Analog-to-Digital Conversion - Quantization - Scalar Quantization

 

Quantization

In the previous section we studied two methods for noiseless coding; that is, compression
of the source output sequence such that full recovery is possible from the
compressed data. In these methods the compressed data are a deterministic function
of the source output, and the source output is also a deterministic function of the compressed
data. This one-to-one correspondence between the compressed data and the
source output means that their entropies are equal and no information is lost in the
encoding-decoding process.

 

In many applications, such as digital processing of the analog signals, where the
source alphabet is not discrete, the number of bits required for representation of each
source output is not finite. In order to process the source output digitally, the source has
to be quantized to a finite number of levels. This process reduces the number of bits to
a finite number but at the same time introduces some distortion. The information lost
in the quantization process can never be recovered.

 

In general, quantization schemes can be classified as scalar quantization and vector
quantization schemes. In scalar quantization each source output is quantized individually,
whereas in vector quantization blocks of source output are quantized.
Scalar quantizers can be further classified as uniform quantizers and nonuniform
quantizers. In uniform quantization, the quantization regions are chosen to have equal
length; in nonuniform quantization, regions of various lengths are allowed. It is clear
that, in general, nonuniform quantizers outperform uniform quantizers.

Scalar Quantization

 

 

 

 

Uniform Quantization

 

 

 

 

 

 

 

 

 

 

 

 

 

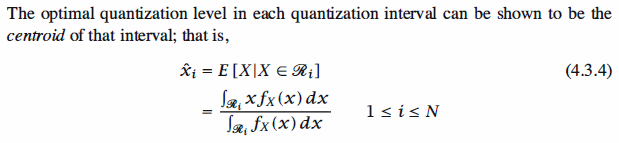
Nonuniform Quantization

 

 

Reference,

　　1. <<Contemporary Communication System using MATLAB>> - John G. Proakis