CCS - Analog-to-Digital Conversion - Measure of Information - Noiseless Coding - Huffman Coding

 

Measure of Information

 

 

 

 

Noiseless Coding

Noiseless coding is the general term for all schemes that reduce the number of bits required
for the representation of a source output for perfect recovery. The noiseless coding
theorem, due to Shannon (1948), states that for perfect reconstruction of a source it

is possible to use a code with a rate as close to the entropy of the source as we desire,
but it is not possible to use a code with a rate less than the source entropy. In other
words, for any€> 0, we can have a code with rate less than H(X) +€,but we cannot
have a code with rate less than H (X), regardless of the complexity of the encoder and
the decoder. There exist various algorithms for noiseless source coding; Huffman coding
and Lempel-Ziv coding are two examples. Here we discuss the Huffman coding
algorithm.

 

Huffman Coding

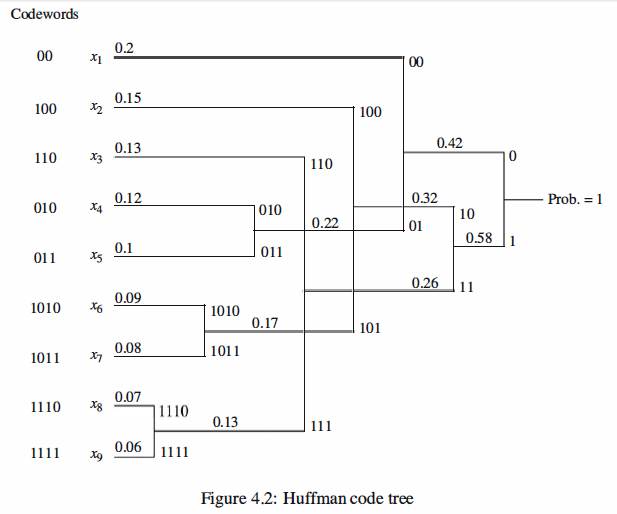
In Huffman coding we assign longer codewords to the less probable source outputs and
shorter codewords to the more probable ones. To do this we start by merging the two
least probable source outputs to generate a new merged output whose probability is the
sum of the corresponding probabilities. This process is repeated until only one merged
output is left. In this way we generate a tree. Starting from the root of the tree and
assigning O's and 1 's to any two branches emerging from the same node, we generate
the code. It can be shown that in this way we generate a code with minimum average
length among the class of prefix-free codes .

 

 

The following example shows how to design a Huffman code.

 

 

 

 

 

 

 

Reference,

　　1. <<Contemporary Communication System using MATLAB>> - John G. Proakis