leetcode 105 从前序与中序遍历序列构造二叉树

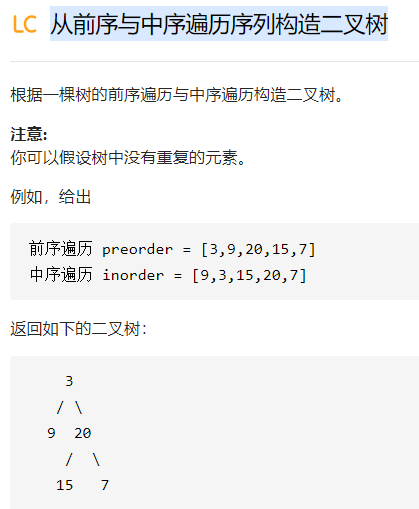
前序遍历 + 中序遍历 = 可复原树
后序遍历 + 中序遍历 = 可复原树
前序遍历 + 后序遍历 = 不可

分析：

前序遍历第一个值即为根节点，但是无法知道左子树有几个节点，也就确定不了左右子树

中序遍历如果能知道根节点，就能知道左子树、右子树各自节点数。

组合两者，由前序得到根节点，再由中序判别左、右子树个数。

设前序数组的左边界为pre_left,右边界为pre_right
中序数组的左边界为ino_left,右边界为ino_right

那么根节点pre_root就为 preoder[pre_left]
在inorder数组中找到preoder[pre_left]这个值，假设它的index为 ino_root
那么左子树个数size_left_subtree为 ino_root-ino_left

其中在inorder数组中找到preoder[pre_left]，可以进行优化，预先遍历一次preoder，将里面的值存到unorder_map中当作Key，将它的index设为val。后续查找的时候直接取即可。

---

这样一来:
左子树:
在preorder中的下标范围为[pre_root+1,pre_root+size_left_subtree]
在inorder中的下标范围为[ino_left,ino_root-1]
右子树:
在preoder中的下标范围为[pre_root+size_left_subtree+1,pre_right]
在inorder中的下标范围为[ino_root+1,ino_right]

很明显，每做一次可以将当前节点创建，然后拆分成左子树、右子树，对于两者分别看成根节点，带入各自范围再进行递归，就可以构造整颗树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    unordered_map<int,int> index;
    TreeNode* buildHelper(vector<int>& preorder, vector<int>& inorder,int pre_left,int pre_right,int ino_left,int ino_right)
    {
        if(pre_left>pre_right||ino_left>ino_right) return nullptr;

        int pre_root = pre_left;

        int ino_root = index[preorder[pre_root]];

        TreeNode* node = new TreeNode(preorder[pre_root]);

        int size_left_subtree = ino_root-ino_left;
        node->left = buildHelper(preorder,inorder,pre_left+1,pre_left+size_left_subtree,ino_left,ino_root-1);
        node->right = buildHelper(preorder,inorder,pre_left+size_left_subtree+1,pre_right,ino_root+1,ino_right);
        return node;
    }
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for(int i = 0; i < n; ++i)
        {
            index[inorder[i]] = i;
        }
        return buildHelper(preorder,inorder,0,n-1,0,n-1);
    }
};