leetcode 264 丑数II

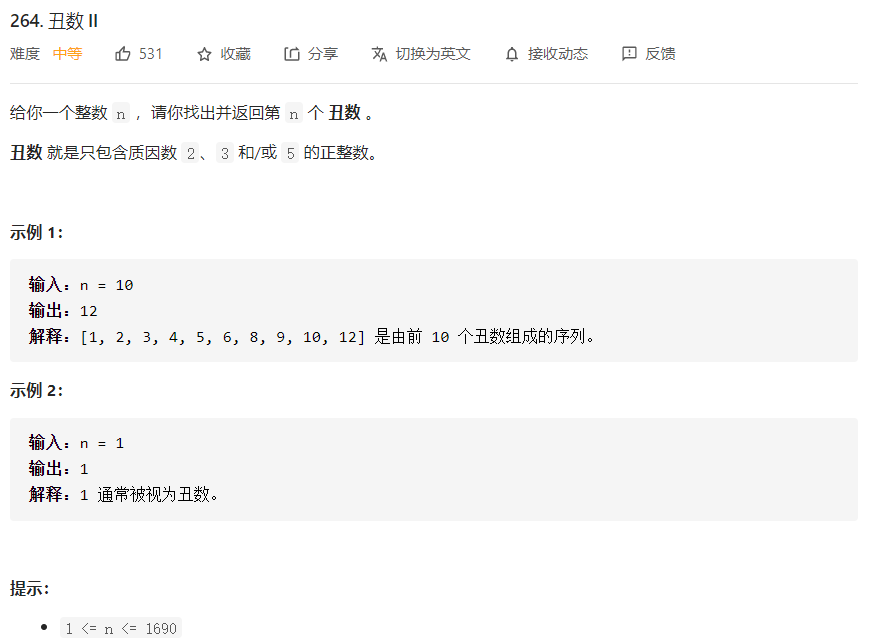
一开始乍一看题，首先就想到了之前做的一个求质数的题，采用的过滤的方式，将已经确定的质数，排除掉这些质数的倍数值。

再仔细一看题给的输入，发现给的不是范围值，就只好想其他办法。

朴素的想法是遍历每个数，判断是否是丑数，是，++count；直到count==n为止。结果就是运行超时。 朴素的想法是遍历每个数，判断是否是丑数，是，++count；直到count==n为止。结果就是运行超时。

后来看了下题解，用三指针，分别指向2的倍数，3的倍数，5的倍数。这不跟我最开始想的思路差不多嘛，哎，还是脑子太死，不灵活。

---

三指针解题思路：
因为要找到第n个值，那就需要有东西来记录一个顺序，来表明到第几个了，朴素思想里用的计数变量，这里采用一个数组dp[n+1]，表示第n个元素为第n个丑数,其中dp[1] = 1(PS:1视为丑数)，dp[n]即为答案。

初始时 p2,p3,p5都指向dp[1]，即均为1。

现在从dp[2]开始填这个数组，因为是按顺序填，所以需要优先填最小的。

int num1 = dp[p2] * 2,num2 = dp[p3] * 3,num3 = dp[p5] * 5;
dp[i] = min(num1,min(num2,num3));

---

填了之后，需要更新三个指针，因为只有一个数被填了，所以实际只更新指向被填进去的数的那个指针

if(dp[i] == num1)
{
   ++p2;
}
if(dp[i] == num2)
{
   ++p3;
}
if(dp[i]==num3)
{
   ++p5;
}

这样就能始终保持填的这个数是目前最小的丑数。
依次填满数组即可，dp[n]就是答案。

可以发现，这种类似过滤的做法，并没有去判断一个数是不是符合某种条件，而是通过已经确定符合条件的值，来确定或者排除某些数，是一个非常迅捷的算法！

上面说过，同样使用过滤做法的题，我还做过一个求质数的题，204. 计数质数